
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення лівих і правих моментних фокусних відношеньСодержание книги
Поиск на нашем сайте
Розглянемо два випадки завантаження нерозрізної балки: а) нерозрізна балка постійної жорсткості завантажена так, що зовнішні сили знаходяться правіше від прольотів, які досліджуються (рис. 2.8).
Рисунок 2.8 Відомо, що від навантаження в будь-якому одному прольоті нерозрізної балки виникає зусилля в інших прольотах. Запишемо рівняння трьох моментів для першої опори:
Оскільки
Поділимо всі члени рівняння на
Після цього, поділимо члени рівняння на величину
Запишемо рівняння трьох моментів для опори 2:
Поділимо всі члени рівняння на
Тобто, ми отримали залежність для визначення лівого моментного фокусного відношення для третього прольоту:
Для будь-якого n -го прольоту можна записати:
Залежність (2.9) є основною формулою для визначення лівих моментних фокусних відношень. Для того, щоб визначити
Рисунок 2.9
Маємо висновок: якщо нерозрізна балка зліва починається шарнірною опорою, то ліве моментне фокусне відношення для першого прольоту дорівнює нескінченності ( Розглянемо балку, яка зліва починається жорстким затисненням (рис. 2.10) і матимемо:
Рисунок 2.10
Тобто: якщо нерозрізна балка зліва починається опорою у вигляді жорсткого затиснення, то ліве моментне фокусне відношення для першого прольоту дорівнює двом (
б) нерозрізна балка постійної жорсткості завантажена так, що зовнішні сили знаходяться лівіше від прольотів, які досліджуються (рис. 2.11).
Рисунок 2.11
Запишемо рівняння трьох моментів для n+ 1 опори:
Оскільки
Поділимо всі члени рівняння на
Після цього, поділимо члени рівняння на величину
Запишемо рівняння трьох моментів для опори n:
Поділимо всі члени рівняння на
Тобто Залежність (2.10) є основною формулою для визначення правих моментних фокусних відношень. Аналогічно можна показати, що коли нерозрізна балка закінчується шарнірною опорою, то праве моментне фокусне відношення останнього прольоту дорівнює нескінченності ( Якщо нерозрізна балка закінчується опорою у вигляді жорсткого затиснення, то праве моментне фокусне відношення для останнього прольоту дорівнює двом ( Залежності (2.9) та (2.10) показують, що величини моментних фокусних відношень не залежать від характеру зовнішнього навантаження на нерозрізну балку, а залежать лише від розмірів її прольотів. Розглянемо простий приклад. Для заданої нерозрізної балки побудувати епюру М (рис. 2.12а). Задана балка три рази статично невизначувана. Якщо її розв`язувати методом сил (рівнянням трьох моментів), тоді необхідно розв`язувати систему з трьох рівнянь.
Рисунок 2.12 Праві моментні фокусні відношення підраховуємо в напрямку справа наліво:
За правими моментними фокусними відношеннями знаходимо всі опорні моменти:
По отриманих значеннях будуємо епюру вигинаючих моментів (рис. 2.12б).
Опорні моменти завантаженого прольоту нерозрізної балки
Аналітичний розрахунок нерозрізної балки при статичному навантаженні в будь-якій формі розрахунку завжди зводиться до визначення її опорних моментів. Від навантажень на консолях опорні моменти легко знайти за правими або лівими моментними фокусними відношеннями. Розглянемо також можливість визначення опорних моментів від навантажень, прикладених в прольотах нерозрізної балки методом фокусів. Розглянемо частину нерозрізної балки (рис. 2.13а), в якій завантажений n -ий прольот і знайдемо лівий та правий опорні моменти цього завантаженого прольоту.
Рисунок 2.13 В межах завантаженого прольоту (рис. 2.13б) необхідно знати фіктивні реакції Запишемо рівняння трьох моментів для опори n- 1 та опори n:
Для прольоту n- 1 можна записати
Підставимо отримані величини в рівняння (2.111) і (2.12):
Розділимо кожний член цих рівнянь на величину
Бачимо, що в квадратних дужках містяться вирази для визначення лівих та правих моментних фокусних відношень Тоді система рівнянь може бути записана:
В отриманій системі рівнянь маємо невідомі опорні моменти завантаженого прольоту. Для практичного використання цих залежностей їх можна дещо змінити. Вирази Тоді система рівнянь прийме такий вигляд:
Розв’язуємо отриману систему рівнянь і одержуємо формули для визначення опорних моментів завантаженого прольоту нерозрізної балки. Лівий опорний момент завантаженого прольоту буде:
Правий опорний момент завантаженого прольоту буде:
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.009 с.) |


 ;
; , тоді
, тоді  .
. :
: .
. і запишемо:
і запишемо: Þ
Þ  , звідки
, звідки  .
.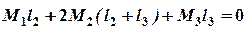 ;
; , підставивши замість М1 його значення, отримане вище:
, підставивши замість М1 його значення, отримане вище: ;
; ;
; ;
;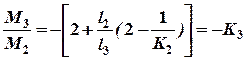 , звідки
, звідки  .
. . (2.8)
. (2.8) . (2.9)
. (2.9)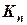 необхідно знати
необхідно знати 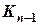 і т. д.
і т. д. Для прольоту
Для прольоту  (див. рис. 2.9) маємо:
(див. рис. 2.9) маємо:  , так як
, так як  .
. ).
). .
.

 ).
).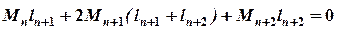 ;
; , тоді
, тоді 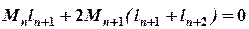 .
. :
: .
. і запишемо:
і запишемо: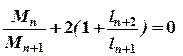 Þ
Þ  , звідки
, звідки  .
.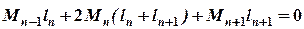 .
. , підставивши замість Мn+ 1, його значення, отримане вище:
, підставивши замість Мn+ 1, його значення, отримане вище: ;
; ;
; , звідки
, звідки  .
. . (2.10)
. (2.10) ).
). ).
). Оскільки, навантаження є лише на лівій консолі балки, скористуємося лише правими моментними фокусними відношеннями, які визначимо за формулою (2.10).
Оскільки, навантаження є лише на лівій консолі балки, скористуємося лише правими моментними фокусними відношеннями, які визначимо за формулою (2.10).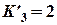 ;
; ;
; .
. кНм;
кНм;  , звідки
, звідки  кНм;
кНм; , звідки
, звідки  кНм;
кНм; , звідки
, звідки  кНм.
кНм.
 та
та  .
.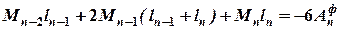 ; (2.11)
; (2.11)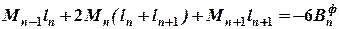 . (2.12)
. (2.12)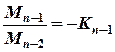 , а для прольоту n+ 1 маємо
, а для прольоту n+ 1 маємо  . Звідки знайдемо:
. Звідки знайдемо: і
і 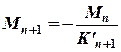 .
. ;
; .
. та винесемо за дужки
та винесемо за дужки  , тобто запишемо їх у такому вигляді:
, тобто запишемо їх у такому вигляді: ;
; .
.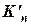 (див. формули (2.9) та (2.10)).
(див. формули (2.9) та (2.10)). ;
; .
. і
і  називають перехресними відрізками й їх легко можна визначити для будь-яких типів навантажень. Значення перехресних відрізків є наведені також і в довідковій літературі.
називають перехресними відрізками й їх легко можна визначити для будь-яких типів навантажень. Значення перехресних відрізків є наведені також і в довідковій літературі. ;
; .
. . (2.13)
. (2.13) . (2.14)
. (2.14)


