
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок розрахунку нерозрізної балки методом фокусів при статичному навантаженніСодержание книги
Поиск на нашем сайте
Підсумовуючи вище викладене, можна запропонувати наступний порядок аналітичного розрахунку нерозрізної балки. Її статичний розрахунок зводиться до визначення внутрішніх зусиль в перерізах тіла, а значить до побудови епюр М і Q. 1. Визначають ступінь статичної невизначеності нерозрізної балки по залежності:
2. Визначаються ліві та праві моментні фокусні відношення для кожного прольоту нерозрізної балки за формулами:
3. Розглядають кожний завантажений прольот нерозрізної балки у вигляді простої балки на двох опорах, будують балочні епюри 4. Від кожного виду навантаження, що діє на нерозрізну балку знаходять величини опорних моментів. Якщо навантаження прикладене на консолях, то опорні моменти знаходять за лівими та правими моментними фокусними відношеннями. Для завантажених прольотів ліві та праві опорні моменти визначають за формулами:
а всі інші опорні моменти від цього ж навантаження визначають за лівими або правими моментними фокусними відношеннями. Підрахунок опорних моментів рекомендується вести в табличній формі (таблиця опорних моментів). 5. Знаючи величини всіх опорних моментів, наносять лінію опорних моментів, а до неї “підвішують” балочні епюри вигинаючих моментів. При цьому, отримують розрахункову епюру вигинаючих моментів 6. Маючи епюру
7. По епюрі
Наносять знайдені величини реакцій на розрахункову схему балки та перевіряють умову рівноваги для всієї балки:
На ділянці рівномірно розподіленого навантаження слід визначити Таблиця 2.1 – Вихідні дані для РГР №2.
Рисунок 2.14 – Варіанти розрахункових схем статично невизначуваної балки для РГР №2.
Продовження рис. 2.14
Для заданої нерозрізної балки (рис. 2.15а) побудувати епюри внутрішніх зусиль (еп.
Порядок розрахунку:
1. Пронумеруємо опори зліва направо від нуля до n та визначимо ступінь статичної невизначеності балки:
тобто балка три рази статично невизначувана. 2. Визначаємо ліві та праві моментні фокусні відношення за формулами:
Результати підрахунку заносимо в таблицю 2.1. Таблиця 2. 1
Нам уже відомо, що в першому прольоті Ліві:
праві:
3. Розглядаємо кожний завантажений прольот нерозрізної балки, як просту балку на двох опорах, будуємо балочні епюри а) Прольот l 1 (рис. 2.16а). Для такого типу навантаження маємо (див. дод.1):
а) б) Прольот l 2 (рис. 2.16 б)
б) б) Рисунок 2.16 Для такого типу навантаження матимемо:
4. Від усіх навантажень, що діють на нерозрізну балку, визначаємо всі опорні моменти, а результати заносимо в таблицю 2.2 (таблиця опорних моментів). Таблиця 2.2- Таблиця опорних моментів.
а) Опорні моменти від навантаження у першому прольоті. Оскільки прольот має навантаження, то опорні моменти для першого прольоту знаходимо за формулами:
Інші опорні моменти від цього ж навантаження визначаємо за правими моментними фокусними відношеннями:
б) Опорні моменти від навантаження у другому прольоті. Оскільки прольот має навантаження, то опорні моменти (лівий та правий) для нього знаходимо за формулами:
Інші опорні моменти від цього ж навантаження визначаємо за правими та лівими моментними фокусними відношеннями в залежності від того, по який бік відносно другого прольоту знаходиться шуканий опорний момент. Отже, через ліве моментне фокусне відношення маємо:
а через праве моментне фокусне відношення маємо:
в) Опорні моменти від навантаження на правій консолі.
Через ліве моментне фокусне відношення знайдемо інші опорні моменти:
Остаточні опорні моменти знайдемо як суму опорних моментів від всіх видів навантажень (таблиця 2.2).
5. За результатами таблиці опорних моментів (табл. 2.2), будують лінію опорних моментів (рис. 2.15б,пунктир). До лінії опорних моментів “підвішують” балочні епюри
6. Маючи епюру
а) Прольот l 1. Для цього прольоту формулу Журавського слід записати для початку прольоту
б) Прольот l 2. Для цього прольоту цю формулу слід записати аналогічно:
в) Прольот l 3. Для третього прольоту, де навантаження відсутнє, матимемо:
7. По епюрі
Якщо нанести знайдені величини реакцій на розрахункову схему балки зі своїми знаками та перевірити умову рівноваги
8. В другому прольоті, де діє рівномірно розподілене навантаження q, знайдемо на епюрі
а для нашого випадку можна записати:
де
Тоді:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.235.104 (0.008 с.) |


 ;
; .
. та
та 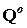 , визначають перехресні відрізки.
, визначають перехресні відрізки. ;
; ,
,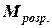
 . При цьому, рекомендується використовувати формулу Журавського:
. При цьому, рекомендується використовувати формулу Журавського: .
. .
.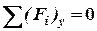 .
. .
. , м
, м
 , м
, м
 , м
, м
 м
м
 кН
кН
 кН
кН
 , кН/м
, кН/м
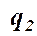 , кН/м
, кН/м
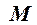 , кНм
, кНм

 - посере-
дині прогону
- посере-
дині прогону




 .
. Рисунок 2.15
Рисунок 2.15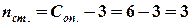 ,
,







 (балка починається затисненням), а в третьому –
(балка починається затисненням), а в третьому –  (балка закінчується шарнірною опорою).
(балка закінчується шарнірною опорою). ,
, ;
;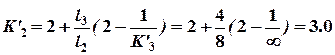 ,
, .
.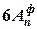 і
і  та перехресні відрізки
та перехресні відрізки  і
і  .
.
 ;
;  .
.
 ;
;  .
.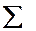
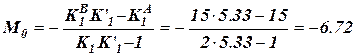 кНм;
кНм;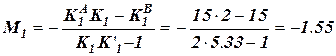 кНм.
кНм. Þ
Þ  кНм;
кНм; Þ
Þ  кНм.
кНм.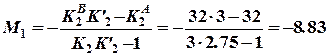 кНм;
кНм; кНм.
кНм. Þ
Þ 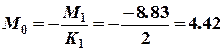 кНм,
кНм,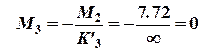 кНм.
кНм. кНм.
кНм. Þ
Þ  кНм;
кНм; Þ
Þ  кНм;
кНм; кНм;
кНм; завантажених прольотів. При цьому, отримують розрахункову епюру вигинаючих моментів
завантажених прольотів. При цьому, отримують розрахункову епюру вигинаючих моментів  і для його кінця
і для його кінця  :
: кН;
кН; кН.
кН.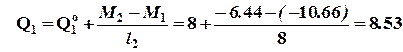 кН;
кН; кН.
кН. кН.
кН. кН;
кН; кН;
кН;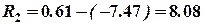 кН;
кН;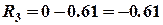 кН.
кН. ;
; 
 максимальний вигинаючий момент за залежностю:
максимальний вигинаючий момент за залежностю: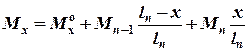 ,
, ,
, – балочний момент (рис. 2.16) на відстані
– балочний момент (рис. 2.16) на відстані  м. від лівої опори. На епюрі
м. від лівої опори. На епюрі  :
: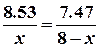 Þ
Þ  Þ
Þ  кНм.
кНм.


