
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Два рази статично невизначуваної плоскої рами методом силСодержание книги
Поиск на нашем сайте
Необхідно: побудувати епюри згинальних моментів М, поперечних Q та поздовжніх N сил від заданого навантаження, а також підібрати поперечні перерізи і перевірити раму на міцність.
а) б) Рисунок 1.2 – а) Задана схема статично невизначуваної рами та б) основна система.
1. Ступінь статичної невизначуваності
2. Система канонічних рівнянь буде мати вигляд:
3. Вибираємо основну систему методу сил, для чого відкидаємо „зайві” зв’язки у вигляді опорних реакцій опори
4. Будуємо вантажну епюру
а) б)
в) г) Рисунок 1.3 – а) вантажний стан основної системи; б) вантажна епюра та г) одинична епюра
а) б)
Рисунок 1.4 – а) одиничний стан №2 та б) одинична епюра 5. Підраховуємо одиничні
За формулою Сімпсона-Корноухова:
За формулою Верещагіна:
За формулою Сімпсона-Корноухова:
За формулою Верещагіна:
6. Виконуємо перевірку знайдених коефіцієнтів системи канонічних рівнянь.
а) построкову:
Рисунок 1.5 – Сумарна одинична епюра
б) універсальну
в) постовпчикову
7. Підставляємо підраховані коефіцієнти в систему канонічних рівнянь і розв’язуємо відносно невідомих
Рисунок 1.6 – Одиничні виправлені епюри
8. Будуємо виправлені епюри, помножаючи ординати одиничних епюр на відповідні значення невідомих (епюру
Одинична епюра
9. Будуємо остаточну розрахункову епюру згинаючих моментів шляхом складання вантажної
епюрами
Рисунок 1.8 – Остаточна епюра Згинаючих моментів
а) статичну шляхом вирізання вузлів С та D.
б) кінематичну
Невелика похибка з’являється в результаті заокруглень при обчисленні.
11. За остаточною епюрою моментів Слід зазначити, що будувати епюри Ділянка ЕС: Ділянка ВД: Ділянка СА: Ділянка СD: Ділянка DK:
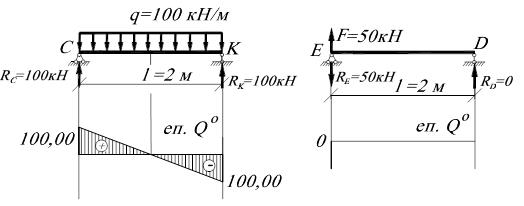
Рисунок 1.9 – Балочні епюри для ділянок СК та ЕD.
Рисунок 1.10 – Остаточні епюри
12. Перевіряємо правильність побудови епюр Вузол С: Вузол D:
13. Підбираємо поперечні перерізи рами у вигляді двотавра. Стрижень ЕА (ригель): Стрижень BK (ригель): Стрижень CD (стійка): За сортаментом підбираємо двотаври: Стрижень ЕА (ригель): двотавр №55 ( Стрижень BK (ригель): двотавр №45 ( Стрижень CD (стійка): двотавр №27 ( або з метою зменшення кількості типорозмірів два двотаври № 45 ( Визначивши розміри, перевіряємо міцність стрижнів: Стрижень ЕА (ригель):; Стрижень BK (ригель): Проте перенапруження складає 1,6 %. Стрижень CD (стійка):
Оскільки умова міцності для стрижня CD не виконується, потрібно підібрати інший переріз. Приймаємо двотавр № 33 (
Отже, остаточно підібрані такі перерізи: стрижень BK (ригель): двотавр № 45; стрижень CD (стійка): двотавр № 33; стрижень ЕА (ригель): двотавр № 55. Приклад розрахунку Плоскої рами замкненого профілю методом сил
Рисунок 1.11 – Задана схема рами замкненого профілю.
1. Ступінь статичної невизначуваності
Перевірка знайдених реакцій:
Отже, реакції знайдено правильно.
2. Система канонічних рівнянь буде мати вигляд:
3. Вибираємо основну систему методу сил, для чого розрізаємо раму між опорами А і В. В даному перерізі виникають невідомі внутрішні зусилля
Рисунок 1.12 – Основна схема рами замкненого профілю.
4. Будуємо вантажну епюру
Рисунок 1.13 – а) вантажний стан основної системи; б) вантажна епюра.
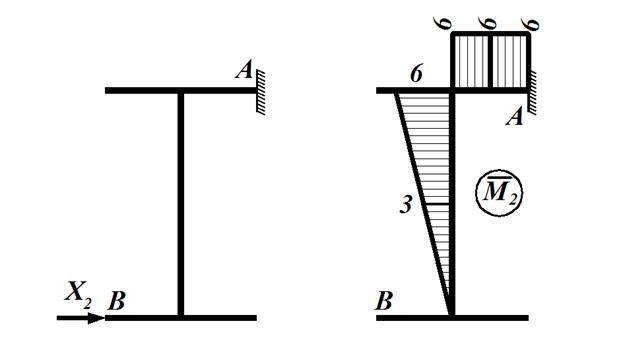
Рисунок 1.14 – а) одиничний стан №1 та б) одинична епюра
Рисунок 1.15 – а) одиничний стан №2 та б) одинична епюра
Рисунок 1.16 – а) одиничний стан №3 та б) одинична епюра
5. Підраховуємо одиничні
6. Перевіряють правильність підрахованих коефіцієнтів системи канонічних рівнянь.
Рисунок 1.17 – Сумарна одинична епюра Універсальна перевірка:
Постовпчикова перевірка:
7. Підставляємо підраховані коефіцієнти в систему канонічних рівнянь і розв’язуємо відносно невідомих
8. Будуємо сумарну виправлену епюру
Рисунок 1.18 – Сумарна виправлена епюра.
9. Будуємо остаточну розрахункову епюру згинаючих моментів
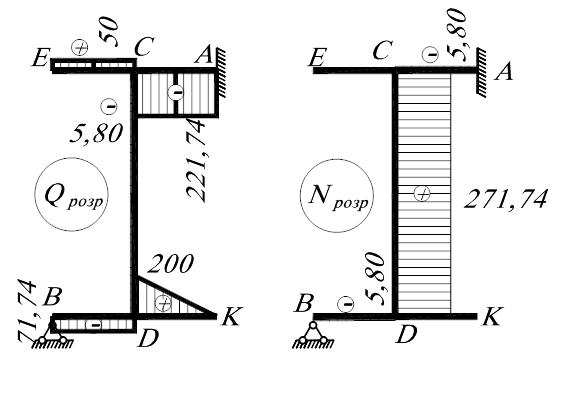
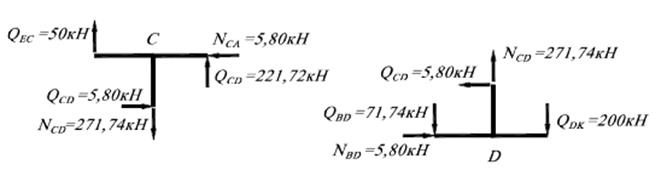
Рисунок 1.17 – а) остаточна епюра згинаючих моментів б) остаточна епюра поперечних сил та балочні епюри (сірим кольором) в) остаточна епюра поздовжніх сил. 10. Виконуємо статичну перевірку правильності побудови епюри Вузол В: Вузол D:
11. За остаточною епюрою моментів Остаточні епюри
Ділянка СD:
Ділянка ЕС: Ділянка AE: Ділянка AB: Ділянка BL: Ділянка LK: Ділянка KD:
12. Будуємо епюру
13. Перевіряємо раму на міцність. В поперечному перерізі згідно завдання запроектований двотавр № 20, який за сортаментом має наступні характеристики:
При перевірці використаємо найбільший згинаючий момент, що діє в перерізі рами (точка В):
Отже, умова міцності виконується.
|
||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.79.73 (0.007 с.) |


 . Тобто рама два рази статично невизначувана.
. Тобто рама два рази статично невизначувана.
 (рис. 1.2б).
(рис. 1.2б). для вантажного стану основної системи. Від одиничної сили
для вантажного стану основної системи. Від одиничної сили  будуємо одиничну епюру
будуємо одиничну епюру  від
від  –
–  .
.

 ; в) одиничний стан №1
; в) одиничний стан №1 .
.
 та вантажні коефіцієнти
та вантажні коефіцієнти 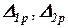 . При підрахунках використовуємо залежність
. При підрахунках використовуємо залежність  (береться з завдання), тобто
(береться з завдання), тобто  . В подальшому приймемо скорочення
. В подальшому приймемо скорочення  .
.
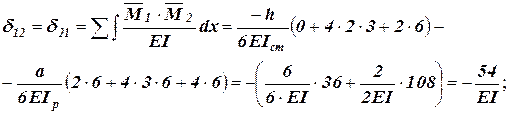




 ;
; ;
; .
.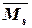
 ;
; ;
;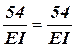 .
.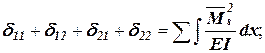

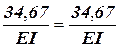 .
.
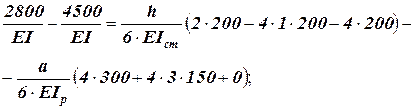

 та
та  . Отже, маємо:
. Отже, маємо:
 .
.
 на
на  (шляхом складання епюр
(шляхом складання епюр  та
та  ) – див. рис. 1.7.
) – див. рис. 1.7. Рисунок 1.7 – Сумарна виправлена
Рисунок 1.7 – Сумарна виправлена
 з сумарною виправленою
з сумарною виправленою 10. Виконуємо перевірку правильності побудови епюри
10. Виконуємо перевірку правильності побудови епюри 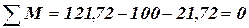


 , використовуючи формулу Журавського. А за епюрою поперечних сил будуємо епюру поздовжніх зусиль
, використовуючи формулу Журавського. А за епюрою поперечних сил будуємо епюру поздовжніх зусиль  .
.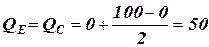 кН;
кН; кН;
кН; кН.
кН. кН;
кН; кН:
кН: 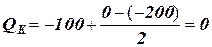 .
.
 та
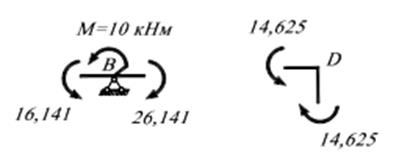
та  шляхом розглядання рівноваги вузлів.
шляхом розглядання рівноваги вузлів.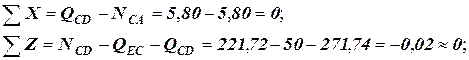

 ;
; ;
; .
. ,
, 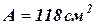 )
) ,
,  )
) ,
,  )
) ).
).
 ;
;
 ,
,  ). Виконаємо перевірку:
). Виконаємо перевірку:
 Необхідно: для заданої рами замкненого профілю побудувати епюри внутрішніх зусиль (
Необхідно: для заданої рами замкненого профілю побудувати епюри внутрішніх зусиль (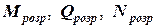 ) від заданого навантаження. Перевірити раму на міцність. Прийняти жорсткості елементів рами постійними, тобто
) від заданого навантаження. Перевірити раму на міцність. Прийняти жорсткості елементів рами постійними, тобто  , а поперечний переріз – двотавр № 20,
, а поперечний переріз – двотавр № 20, 
 . Тобто рама три рази статично невизначувана. Знаходимо опорні реакції
. Тобто рама три рази статично невизначувана. Знаходимо опорні реакції  , використовуючи рівняння статики:
, використовуючи рівняння статики:


 ,
, 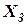 та
та 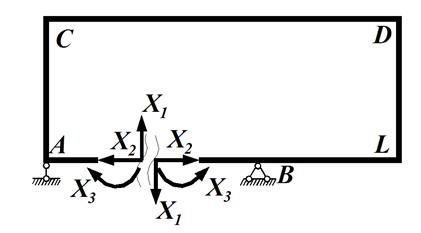
 –
–  .
.


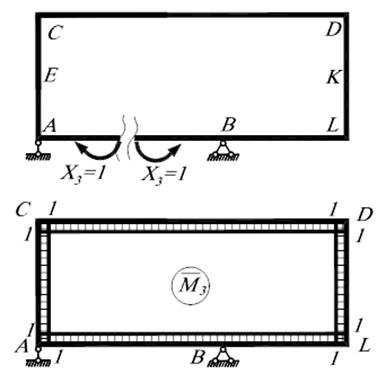
 та вантажні коефіцієнти
та вантажні коефіцієнти  . Враховуємо, що
. Враховуємо, що  ,
,  ,
, 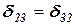 .
. 



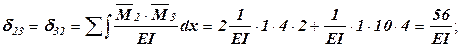




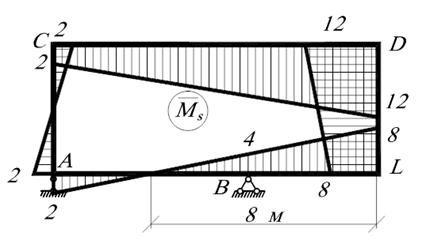

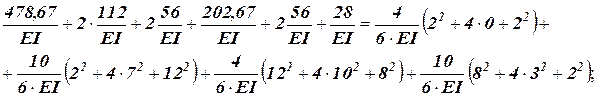
 .
.

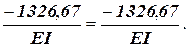
 та
та  . Отже, маємо:
. Отже, маємо: .
.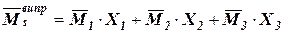 .
.



 кН;
кН;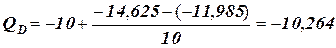 кН;
кН;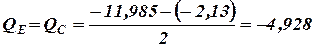 кН;
кН; кН;
кН; кН;
кН;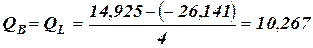 кН;
кН;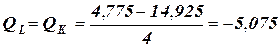 кН;
кН;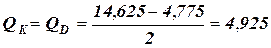 кН.
кН. .
.
 ,
,  .
. , а також значення поздовжньої сили в цій точці
, а також значення поздовжньої сили в цій точці  .
.



