Приклад побудови логарифмічних частотних характеристик вихідної, скоректованої САУ та коректуючого пристрою у середовищі Matlab 6.0

На рисунку 3.1 наведений можливий текст М-файлу для побудови ЛАЧХ нескоректованої, бажаної системи та ЛАЧХ коректуючого пристрою. Для прикладу обрана система автоматичного управління третього порядку з першим порядком астатизму, яка складається із однієї інтегруючої та двох аперіодичних ланок першого порядку. Функція передачі вихідної нескоректованої системи має наступний вигляд:

У логарифмічному нулі, 20lg(1)=0 ордината ЛАЧХ нескоректованої системи L(1)=20(600)»56дБ, Частоти злому даної ЛАЧХ визначаються згідно заданих постійних часу аперіодичних ланок – w₁=1/T1=1/0.024»41.7 (c^-1), w₂=1/T2=1/0.004»250 (c^-1). Для побудови ЛАЧХ нескоректованої системи використовується оператор циклу for з вкладеною конструкцією умовного оператора if…else (оператори 1-12).

Для побудови ЛАЧХ бажаної системи спочатку визначається нова частота зрізу w_ЗР, яка пов’язана через номограми з показниками якості перехідного процесу скоректованої системи – часом регулювання t_ПП=1с та перерегулюванням s%=40%, і дорівнює:

Ліва та права граничні частоти середньо частотної ділянки бажаної ЛАЧХ обираються згідно необхідних запасів стійкості скоректованої системи за фазою та амплітудою – w_ЛІВ=5.27 (с^-1), w_ПР=250 (с^-1). Низькочастотна ділянка нескоректованої системи спрягається з бажаною ЛАЧХ асимптотою з нахилом -60 дБ/дек. Високочастотна ділянка бажаної ЛАЧХ паралельна ЛАЧХ вихідної системи. Побудові бажаної ЛАЧХ відповідає текст М-файлу з 13 по 22 оператор включно. ЛАЧХ коректуючої ланки отримана, як різниця між бажаної ЛАЧХ та ЛАЧХ вихідної нескоректованої системи – L_К(w)=L_Б(w)-L_ВИХ(w). Для побудови графіків ЛАЧХ в полулогарифмічному масштабі використаний оператор semilogx. Результати побудови наведені на рисунку 3.2.

Для перевірки правильного розрахунку параметрів коректуючого пристрою та результатів корекції слід у текст М-файлу добавити наступні оператори:

 

sysV=tf(600,[1 0])*tf(1,[0.024 1])*tf(1,[0.004 1])–функція передачі вихідної САУ;

sysk1=tf([0.19 1],[1 1])

sysk2=sysk1*sysk1 – функція передачі 1-ого ланцюга коректуючої ланки;

sysk3=tf([0.024 1],[0.004 1])–функція передачі 2-го ланцюга коректуючої ланки;

sysK=sysk2*sysk3 – функція передачі коректуючого пристрою;

sysSK=sysV*sysK – функція передачі скоректованої розімкнутої САУ;

sysSKZ=feedback(sysSK,1) – функція передачі скоректованої замкнутої системи;

step(sysSK),grid – побудова перехідної характеристики скоректованої САУ.

 

 

 

 

Рисунок 3.1 – Текст М-файлу побудови ЛАЧХ вихідної, скоректованої систем та ЛАЧХ коректуючого пристрою

Цей текст програми відповідає моделюванню послідовного з’єднання вихідної системи з коректуючим пристроєм наступного вигляду:

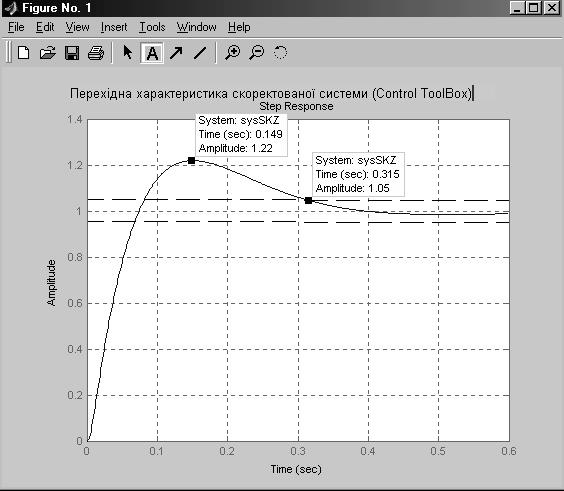
з подальшою побудовою перехідної характеристики, якщо перша ітерація скоректованої системи не дозволяє наблизитися до оптимального перехідного процесу, слід змінити частоту зрізу, ліву та праву границю середньо-частотної ділянки та нахил асимптоти спряження із низькочастотною ділянкою нескоректованої системи. Результати побудови результуючої перехідної характеристики наведені на рисунку 3.3, як бачимо час регулювання у перехідному процесі для замкнутої скоректованої системи t_ПП=0.31с, перерегулювання s%=22%. Такі показники якості є приємлемими для того, щоб система САУ знайшла практичне застосування, якщо показники якості задовільняють поставленому практичному завданню, то процедуру синтезу слід рахувати завершеною.

 

 

Рисунок 3.2 – Результати побудови ЛАЧХ у полулогарифмічному масштабі

 

Наведені тексти програм на мові, убудованій у середовище MatLab 6.0, можуть бути основою для проведення як прцедури аналізу, так і процедури синтезу САУ на кожному ітераційному кроці наближення системи до заданих оптимальних показників якості. Наприклад, можливе проведення повного аналізу замкнутої скоректованої системи. Для цього достатньо у текст програми добавити оператор виклику інтерактивного графічного редактора ltiview,імпортувати у його середовище модель замкнутої або розімкнутої скоректованої САУ та провести аналіз їх властивостей. або за виглядом діаграми bode, або за годографом Найквіста, обо зі іншими відомими динамічними характеристиками. Можливостям ППП MatLab 6.0 для моделювання, аналізу та синтезу лінійних САУ присвячений цілий ряд методичних розробок [2, 9, 10 10, 11 12], при виконанні розрахунково-графічної роботи студенти повінні самостійно вивчити окремі методи дослідження лінійних САУ, набути навики побудови таких характеристик, як годограф Михайлова, кореневий годограф, крива Д-розбиття, фазова площина, вміти визначати показники якості процесів регулювання по побудованим АЧХ та ДЧХ замкнутої системи, діаграмі розтошування коренів характеристичного рівняння на комплексній площині. Відмічені аспекти дозволяють студенту отримати максимальну оцінку при здачі графічно-розрахункової роботи, так як свідчать про творчий підхід прив виконання поставленого завдання. Перелік питань, які перераховані у постановці завдання стосуються лише обо’язкових знань, що дозволяють студенту отримати задовільну оцінку. При виставленні оцінки за виконання графічно-розрахункової роботи враховується також вміння оформити результати розрахунків, наявність необхідних коментарів на побудованих графіків, перевірка отриманих результатів у моделюочому середовищі Simulink, який слід рахувати імітаційним віртуальним стендом для симуляції САУ [9, 10, 11, 12].

 

Рисунок 3.3 – Перехідна характеристика соректованої системи

На рисунку 3.4 наведена структурна схема скоректованої замкнутої системи з включеним послідовно коректуючим пристроєм та пі’єдними пристроями – генератором одиничної сходинкової дії та осцилографом. Схема зібрана у середовищі Simulink. Результати симуляції наведені на рисунку 3.5, результати співпадають із результататми отриманими у середовищі Control ToolBox.

 

Рисунок 3.4 – Структурна схема синтезованої САУ у середовищі Simulink

 

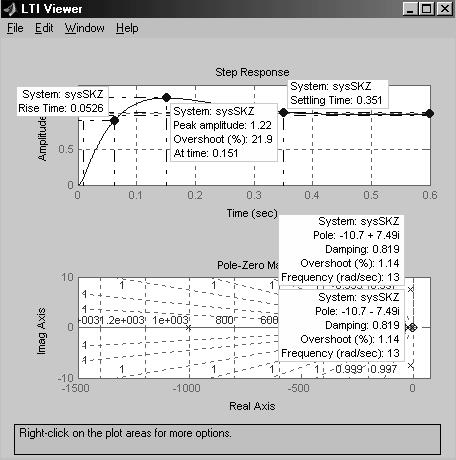
Рисунок 3.5 – Результати тестування скоректованої системи у середовищі Simulink

На рисунку 3.6 наведені ЛАЧХ та ЛФЧХ та годограф Найквіста скоректованої розімкнутої системи. У графічному інтерактивному режимі користувачу доступні опції для вихначення на даних характеристиках точок небезпечних з точки зору стійкості системи. Так, ми бачимо, що скоректована система має достатні запаси стійкості за амплітудою та фазою – DL(480)=34.8дБ, Dj(22.7)=62.4⁰. Годограф Найквіста не охоплює точку з координатами (-1, j0), що підтверджує висновок щодо стійкості замкнутої синтезованої системи.

На рисунку 3.7 наведені графіки перехідної характеристики синтезованої САУ та діаграма розтошування коренів характеристичного рівняння цієї системи на крмплексній площині. Окрім вже вказаних показників якості, на графіку також позначені час досягнення вихідною регульованою величиною перший раз усталеного значеня (t₁=0.0526c) та час досягнення максимального відхилення (t_max=0.151c). На діаграмі розтошування нулів та полюсів функції передачі замкнутої скоректованої САУ на комплексній площині вказані значення дійсних та уявниї частин коренів, які розтошовані найближче до уявної вісі. Корені з додатньою дійсною частиною відсутні, що є необхідною та достатньою умовою стійкості САУ [3, 7].

Рисунок 3.6 – Частотні характеристики розімкнутої синтезованої системи

На рисунку 3.7 наведені графіки перехідної характеристики синтезованої САУ та діаграма розтошування коренів характеристичного рівняння цієї системи на крмплексній площині. Окрім вже вказаних показників якості, на графіку також позначені час досягнення вихідною регульованою величиною перший раз усталеного значеня (t₁=0.0526c) та час досягнення максимального відхилення (t_max=0.151c). На діаграмі розтошування нулів та полюсів функції передачі замкнутої скоректованої САУ на комплексній площині вказані значення дійсних та уявниї частин коренів, які розтошовані найближче до уявної вісі. Корені з додатньою дійсною частиною відсутні, що є необхідною та достатньою умовою стійкості САУ [3, 7].

Наведені приклади дослідження динаміки лінійних САУ та методів їх синтезу слід рахувати лише початковою інформацією для проведення розрахунків та інженерних досліджень, можливості ППП Matlab дійсно неосяжні для того, щоб їх перелічити у даних методичних вказівках. Студентам пропонується, наприклад, звернутися до ППП Siso Desing Tool, Control Tool Identification та іншим спеціалізованим додаткам даного програмного середовища [2, 12].

 

Рисунок 3.7 – Характеристики замкнутої синтезованої САУ