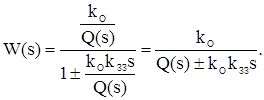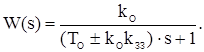Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи корекції, послідовні та паралельні коректуючі пристрої, функції передачі, структурні та електричні схемиСодержание книги
Поиск на нашем сайте У системі автоматичного управління завжди може бути явно виділені незмінна частина і частина системи, у яку можна вносити корективи. Незмінна частина системи обмежує можливість одержання необхідної якості регулювання в тому змісті, що іноді потрібно вносити елементи, які важко реалізувати технічно, якщо їх відносити до самого об’єкта управління. Зрозуміло, що необхідні запаси стійкості і показники якості перехідного процесу забезпечуються за рахунок послідовного або паралельного включення з основними ланками відповідних коректуючих ланок, а також введенням додаткових зворотних зв'язків. Найчастіше послідовні коректуючі ланки включаються між двома інтегруючими ланками. В деяких випадках система без коректуючих ланок взагалі не може працювати, оскільки вона є структурно нестійкою, тобто має таку структуру, при якій годограф амплитудно-фазової характеристики при будь-якому підсиленні в контурі регулювання (управління) охоплює точку з координатами (-1, j0). Прикладом може служити система, що містить дві інтегруючих ланки, які з’єднані послідовно [4, 7]. Коректуючі пристрої використовуються також для зміни смуги пропускання системи, що дозволяє зменшити вплив перешкод. Коректуючі ланки мають особливо підібрані функції передачі. Найбільше застосування одержали наступні послідовні коректуючі ланки: пропорційно-диференціюючі, пропорційно-інтегруючі, пропорційно-інтегро-діференцюючі [3, 4]. Функція передачі ідеальної пропорційно-диференцюючої ланки має вигляд: WПД(s)= Звідси видно, що її вихідна величина містить дві складові – пропорційну вхідній величині, яка визначається коефіцієнтом kП, і пропорційну першій похідній вхідної величини з коефіцієнтом пропорційності kД. Включення пропорційно-диференцюючої ланки в САУ призводить до того, що передавальна функція системи стає рівною: WСК(s)= де WСК(s) – функція передачі синтезованої (скоректованої) системи, WНСК(s) – функція передачі системи, яка підлягає корекції з метою надання її необхідних динамічних властивостей. Покажемо за допомогою амплитудно-фазових характеристик (АФЧХ), який ефект може бути досягнутий при введенні похідної в систему автоматичного управління. На рисунку 2.1 (крива а) зображена амплитудно-фазова характеристика нестійкої САУ. При включенні пропорційно-диференціючої ланки амплитудно-фазова характеристика системи прийме вигляд: WСК(jw)= Якщо kП=1, тоді вираз (2.3) приймає наступний вигляд: WСК(jw)=(1+kД× jw)×WНСК(jw)= WНСК(jw)+ kД×(jw)×WНСК(jw), (2.4)
Рисунок 2.1 – АФЧХ вихідної та системи з ПД коректуючим пристроєм
З виразу (2.4) видно, що WСК(jw) (крива б на рисунку 2.1) може бути отримана з WНСК(jw) (крива а на рисунку 1.1), якщо в кожній точці кривої а до вектора WСК(jw) додати перпендикулярний до нього (під кутом p/2) вектор, довжина якого в kД раз більше довжини вектора WНСК(jw). Таким чином, за рахунок складової kД× jw)×WНСК(jw) вектор випереджає WНСК(jw) на кут, залежний від коефіцієнта kД і частоти w. Це якраз і є необхідним для того, щоб крива б не охоплювала точку з координатами (-1,j0), тобто щоб система стала стійкою.
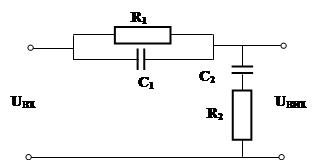
Рисунок 2.2 – Залежність часу регулювання від коефіцієнта диференціювання коректуючої ланки На рисунку 2.2 приведені перехідні характеристики послідовного з'єднання ланок. З характеристик видно, що додаткова позитивна дія по похідній підвищує швидкодію системи, причому із збільшенням коефіцієнта передачі kД швидкодія системи зростає. Практично пропорційно-диференціюючі ланки мають істотну інерційність, їх електричний аналогом є пасивний чотириполюсник на RC- елементах (рисунок 2.3), а функція передачі, із врахуванням інерційності, набуває наступного вигляду:
Інерційну пропорційно-диференційну ланку можна представити як послідовне з'єднання ідеальної пропорційно-диференціючої і звичної інерційної ланок. Тому, все сказане вище про вплив ідеальної пропорційно-диференційної ланки на стійкість і якість перехідного процесу справедливо і для інерційної ланки такого типу з тією лише різницею, що остання ланка повільніше впливає на швидкодію системи і відповідно на її стійкість.
Для ланцюгів корекції в САУ застосовуються також інтегруючі ланки. Як нам вже відомо, введення однієї інтегруючої ланки перетворює статичну систему в астатичну – з астатизмом 1-го порядку, яка не має сталої (статичної) похибки по регульованій координаті, якщо на вході системи постійна вхідна дія. При введенні додатково ще однієї інтегруючої ланки порядок астатизма системи збільшується до 2-го, і система не має сталої швидкісної похибки.
Рисунок 2.4 – АФЧХ вихідної та системи з інтегруючим коректуючим пристроєм На рисунку 2.5 наведений електричний аналог інтегруючого ланцюга, який не змінює порядку астатизму системи, і його номінали. Функція передачі такого коректуючого пристрою має наступний вигляд:
де T2 – постійна часу випередження коректуючого контуру, T1 – постійна часу відставання.
 ; ;
T1 > T2 Þ k =20lg(1/T2) < 1.
Рисунок 2.5 – RC-ланцюг інтегруючої ланки На практиці для корекції САР часто застосовують інтегро-диференцюючі ланцюги. Функція передачі такого коректуючого пристрою має наступний вираз:
Такі коректуючі пристрої поводять себе як інтегруючі у області низьких частот, у області високих частот мають властивості, які наближаються до властивостей диференційних ланцюгів, а в області середніх частот привносить згасання, яке дорівнює 20lga. Це легко побачити на рисунку 2.6, де зображена ЛАЧХ інтегро-диференцюючого ланцюга.
Рисунок 2.6 – ЛАЧХ інтегро-диференціюючого пристрою
Рисунок 2.7 – RC- ланцюг інтегро-диференціюючої ланки Другим класом коректуючих пристроїв є паралельні коректуючі пристрої, які реалізуються у вигляді місцевих зворотних зв'язків, що охоплюють одну або декілька ланок системи. Розрізняють два види зворотних зв'язків: – гнучкий, при якому передаються похідні вихідної величини цієї групи ланок. Гнучкий зворотний зв'язок впливає на систему тільки при перехідних процесах, тобто коли вихідний сигнал міняється в часі. Функцію передачі частини системи W(s) зі зворотним зв'язком через коректуючу ланку з функцією передачі WЗЗ(s) одержуємо, використовуючи відомий вираз:
Розглянемо спочатку дію ідеального жорсткого зворотнього зв'язку. Функція передачі коректуючої ланки у цьому випадку дорівнює WЗЗ(s)=kЗЗ. У випадку, коли цей зворотний зв'язок охоплює звичайну аперіодичну ланку з функцією передачі:
отримаємо наступну функцію передачі скоректованого ланцюга вихідної системи:
Таким чином, в результаті обхвату аперіодичної ланки жорстким зворотним зв'язком її постійна часу і коефіцієнт передачі змінюються в (1±k0kЗЗ) раз, тобто вони зменшуються у разі від’ємного зворотнього зв'язку і збільшуються при позитивному зв’язку. Як коректуючий зворотний зв'язок застосовується, в основному, від’ємний зворотний зв'язок для зменшення інерційності. Від’ємний зворотний зв'язок має і інші переваги: зменшує нелінійність статичної характеристики ланки (або цілого ланцюга), нестабільність її параметрів в часі, а також зменшує рівень шумів на виході ланки. Як приклад гнучкого зворотного зв'язку розглянемо зворотний зв'язок у вигляді ідеальної диференціюючої ланки. Це випадок так званого ідеального гнучкого зворотного зв'язку або зворотного зв'язку по швидкості: WЗЗ(s)=kЗЗ×s.
де Q(s) – поліном знаменника функції передачі ланцюга системи, який підлягає корекції, маємо наступну функцію передачі скоректованого ланцюга:
Отже, гнучкий зворотний зв'язок, не впливаючи на коефіцієнт передачі охоплюваної зворотним зв'язком ланки, змінює коефіцієнт при першому степені оператора Лапласа s в знаменнику її функції передачі. У разі аперіодичної ланки 1-го порядку отримаємо наступну функцію передачі скоректованого ланцюга:
Тобто постійна часу ланки змінюється на величину, яка пропорційна коефіцієнту зворотнього зв'язку, причому від’ємний зворотний зв'язок збільшує постійну часу, а позитивний – зменшує. При цьому на відміну від від’ємного жорсткого зворотнього зв'язку, з'являється можливість підвищення швидкодії без зниження коефіцієнта передачі ланки.
|
||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

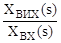 =kП+kД×s. (2.1)
=kП+kД×s. (2.1) =(kП+kД×s)×WНСК(s), (2.2)
=(kП+kД×s)×WНСК(s), (2.2)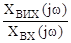 =(kП+kД× jw)×WНСК(jw), (2.3)
=(kП+kД× jw)×WНСК(jw), (2.3)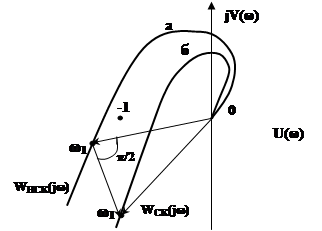

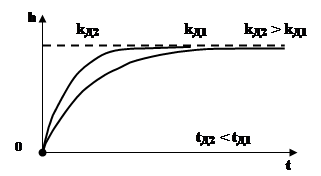 При правильно вибраному значенні kД можна зробити систему не тільки стійкою, але і добитися найкращої можливої для даної системи процесів регулювання або управління. Слід зазначити, що при введенні похідних система стає більш чутливою до високо частотних перешкод.
При правильно вибраному значенні kД можна зробити систему не тільки стійкою, але і добитися найкращої можливої для даної системи процесів регулювання або управління. Слід зазначити, що при введенні похідних система стає більш чутливою до високо частотних перешкод.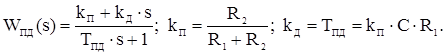 (2.5)
(2.5)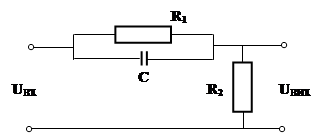
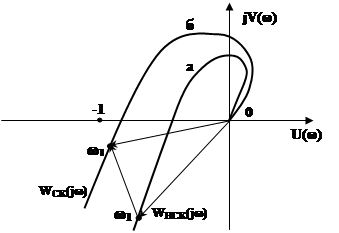
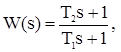 (2.6)
(2.6) T2=R2C2; T1=C(R1+R2);
T2=R2C2; T1=C(R1+R2);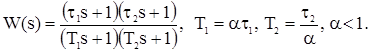 (2.7)
(2.7)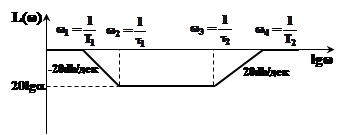
 АФЧХ такого контуру являє собою коло з центром на додатній дійсній осі, яке знаходиться на відстані a від уявної вісі. На рисунку 2.7 а наведений електричний аналог такого коректуючого пристрою.
АФЧХ такого контуру являє собою коло з центром на додатній дійсній осі, яке знаходиться на відстані a від уявної вісі. На рисунку 2.7 а наведений електричний аналог такого коректуючого пристрою. (2.8)
(2.8)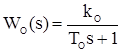 , (2.9)
, (2.9)
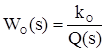 , (2.10)
, (2.10)