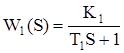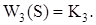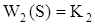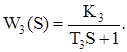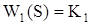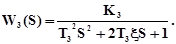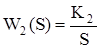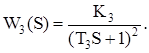Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мета та організація виконання розрахунково–графічної роботиСодержание книги
Поиск на нашем сайте
ЗМІСТ Вступ.............................................................................................................. 4 1. Мета та організація виконання роботи.................................................... 6 2. Основні теоретичні відомості................................................................... 8 2.1. Поняття синтезу систем САУ, постановка задачі, зв’язок з задачами аналізу та моделювання систем............................................................................................. 8 2.2. Способи корекції САУ, послідовні та паралельні коректуючі пристрої, функції передачі, структурні та електричні схеми............................................... 11 2.3. Вихідні дані при постановці завдання синтезу САУ......................... 18 2.4. Методи синтезу послідовних коректуючих пристроїв...................... 20 2.5. Технічна реалізація послідовних коректуючих пристроїв............... 32 3. Приклад побудови логарифмічних частотних характеристик вихідної, скоректованої системи та коректуючого пристрою у середовищі Matlab 6.0. 38 4. Методичний приклад розрахунку параметрів електричної схеми коректуючого пристрою, її розробки та симуляції у середовищі Micro-Cap.......................... 46 5. Завдання на роботу.................................................................................. 50 5.1. Вибір завдання.................................................................................... 50 5.2. Завдання.............................................................................................. 50 Список літератури..................................................................................... 55
ВСТУП Створення й удосконалювання систем автоматичного управління (САУ) є однією з важливих проблем, рішення якої багато в чому визначає рівень розвитку науки і техніки. Тому задача створення якісно нових САУ, що забезпечують високу точність управління й адаптації є актуальною, зі збільшенням жорсткості умов експлуатації систем управління висуваються додаткові вимоги до їхніх якісних показників. У цих умовах, при заданих обмеженнях на експлуатацію системи, стає необхідною побудова оптимальних САУ, що забезпечують мінімальну похибку при наявності змінних у часі впливів. При цьому вхідні впливи є випадковими функціями часу. Рішення задачі оптимізації (синтезу) САУ дозволяє знайти оптимальне управління якістю системи вже на стадії її проектування. Задача синтезу системи автоматичного управління (САУ) розглядається як задача визначення структури і параметрів моделі системи, що забезпечує оптимум заздалегідь обраного критерію якості при наявності впливів і заданих обмеженнях на роботу системи [1, 3, 4]. Якість регулювання та управління у системі можна істотно підвищити, однак ця задача набагато складніше, ніж задача моделювання і, узагалі, аналізу систем автоматичного управління. Корекція системи автоматичного регулювання та управління (САР та САУ) повинна забезпечити необхідні динамічні характеристики системи, тобто задані запаси стійкості і показники якості перехідного процесу. Корекція системи відноситься до області синтезу систем, оскільки при розрахунку корекції потрібно з'ясувати, які додаткові ланки повинні бути введені в систему для забезпечення заданих характеристик. ТАУ дає набір стандартних методів синтезу систем із заданою якістю. Класичним методом цього ряду є метод діаграм В.В.Солодовнікова. Цей метод оперує частотними характеристиками САУ і використовується при виконанні графічно-розрахункової роботи “Синтез послідовного коректуючого пристрою лінійної САУ методом В.В.Солодовнікова”. Розглянуті раніше у лекційному курсі, на практичних та лабораторних заняттях способи підвищення точності і запасів стійкості (демпфування) САУ та САР повинні бути твердо засвоєні студентами до початку виконання графічно-розрахункової роботи з метою, по-перше, розумінні поняття показників якості замкнутої системи, що є вихідними даними завдання на проектування системи, по-друге, можливості використання інших методів досягнення даної якості регулювання у системі. При виконанні додаткового (факультативного) завдання, студенти можуть скористатися методом типових бажаних ЛАЧХ (Сіньковського-Сігалова), методом побудови амплітудо-частотних характеристик, перейти від метода послідовної корекції до метода корекції шляхом введення додаткових зворотних зв’язків. Графічно-розрахункова робота поділяється на три частини: 1. Визначення, за заданими показниками якості, методом В.В.Солодовнікова логарифмічно амплітудно-частотної характеристики (ЛАЧХ) скоректованої системи. Перевірку показників якості перехідної характеристики скоректованої системи у середовищі MatLab 6.0 При виконання цієї частини завдання студенти повинні використовувати наступні прикладні програмні пакети (ППП) середовища MatLab: – ППП Simulink моделювання та дослідження поведінки динамічних САУ у візуальному діалоговому режимі шляхом графічної зборки схеми з’єднань елементарних ланок із стандартних бібліотек; – ППП Control ToolBox створення моделі стаціонарної лінійної САУ програмним шляхом у формі матриць простору станів, у вигляді коефіцієнтів чисельника та знаменника функцій передачі та у формі завдання нулів, полюсів та коефіцієнта передачі моделі системи. 2. Визначення ЛАЧХ коректуючої ланки, як різниці між ЛАЧХ скоректованої (бажаної) системи та ЛАЧХ вихідної САУ. Друга частина виконується у випадку позитивного виконання першої частини завдання. У ППП Simulink знов перевіряються показники якості САУ при послідовному з’єднання моделі коректуючого пристрою та незмінної частини системи. 3. Визначення електричного аналогу коректуючого пристрою. У вигляді пасивного чотириполюсника на RC-елементах або схеми з використанням операційного підсилювача (ОС). Розрахунок параметрів електричної схеми та її моделювання у середовищі WorkBench. Необхідні відомості по початкам програмування у середовища МatLab 6.0 та опису вказаних ППП можна знайти у методичному посібнику та методичних вказівках, які внесені у список літератури.
Основні теоретичні відомості Рисунок 2.9 – Структурна схема ПІД-ругулятора Вплив підсилюючої складової Кп дозволяє змінити загальний коефіцієнт підсилення системи, тим самим дозволяє змінити зменшити коефіцієнт статизму (встановлену похибку)
Вплив інтегруючої складової Кп/s призводить до підвищення порядку астатизму скоректованої системи на одиницю. Її вплив на годограф разове, систематичне. Диференціююча складова Кд не впливає на встановлену похибку:
Збільшення коефіцієнта підсилення Кд підвищує запас стійкості скоректованої системи, згладжує перехідний процес, тому диференціальну складову називають демпфуванням. Таким чином, за допомогою інтегральної і пропорційної складових можна забезпечити перший порядок астатизму і бажану статичну точність системи з одночасним зменшенням запасів стійкості. А диференціальна складова підвищує запас стійкості скоректованої системи. В основі синтезу послідовного корректуючого пристрою, який повинні засвоїти студенти, покладені частотні оцінки показників якості процесів регулювання у лінійній системі і синтез коректуючих пристроїв методом логарифмічних частотних характеристик за допомогою діаграм В.В.Солодовнікова. Метод В.В.Солодовнікова використовує прямий зв'язок між частотною характеристикою і перехідною характеристикою у САУ (САР) [3, 4, 5]:
У цій формуліР(w) – дійсна частина АФЧХ (комплексної функції передачі замкнутої системи): W(jw) = P(w) + jQ(w). В.В. Солодовників довів, що в будь-який САУ зберігаються наступні залежності між основними показниками якості перехідної характеристики і ДЧХ – Р(w): – Якщо ДЧХ при деякому значенні wК має розрив неперервності (Р(w)=¥), це означає наявність уявного кореня si=±jwK у характеристичному рівнянні замкнутої системи і знаходження САУ на межі стійкості. – Наявність високого, гострого піку ДЧХ, а також зміна її знаку свідчать про довготривале згасання коливного процесу. – Перерегулювання s% > 18%, якщо дійсна частотна характеристика (ДЧХ) замкнутої системи Р(w) має максимум, тобто. Рмах > Р0 (рис. 2.10). – Перерегулювання s% < 18%, якщо ДЧХ не має максимуму і є не зростаючою функцією (Р(w)>0 при – Перерегулювання s% = 0, якщо похідна dР/dw <0 і ДЧХ монотонно убуває і Р(w)>0. Вимога монотонного убування ДЧХ часто є занадто жорсткою умовою при вирішенні задач синтезу САУ і накладає невиправдані обмеження на структуру системи та конструкцію її основних елементів. Прийнято забезпечувати перерегулюванняу межах 18 < s% < 40%. Тоді максимальне значення перерегулювання (у %) можна дістати з формулою:
– Якщо Р(w) є приблизно трапецеїдальною характеристикою, тоді тривалість перехідної характеристики знаходитиметься у межах:
– Якщо ДЧХ має максимум, то час перехідного процесу оцінюється наступним виразом:
Крім того, у технічній літературі наводяться криві, за якими залежно від величини Pmax(w)/P(0) можна знайти значення перерегулювання s% та відносного часу регулювання t=wЗtПП. Відомі також номограми, які встановлюють взаємозалежність ординат дійсної та уявної частотних характеристик замкнутої системи та ЛАЧХ розімкнутої системи, а також діаграми зв’язку між перерегулюванням s%, коливальністю М, показниками ступеня затухання і запасів стійкості замкнутої системи. Одним з найефективніших інженерних методів синтезу систем автоматичного управління є метод, в основу якого покладено використання ЛАЧХ розімкнутої системи. Ідея методу ґрунтується на тому, що для стійких мінімально-фазових систем існує однозначний зв'язок між перехідною характеристикою замкнутої системи і виглядом ЛАЧХ відповідної розімкнутої системи. Виходячи з бажаного вигляду перехідного процесу, будують ЛАЧХ, яка відповідає такому процесу (бажану ЛАЧХ). Далі, знаючи вигляд бажаної ЛАЧХ, до неї наближують ЛАЧХ вихідної системи, запроваджуючи різні коректуючі пристрої. Будь-яка САУ складається з незмінної частини, до якої належить об’єкт регулювання або управління, автоматичний управляючий пристрій або регулятор, силовий керований перетворювач, а також елементи головного зворотного зв'язку та порівняння. Об’кт регулювання вважається відомим при проектуванні САК, виконавчий елемент управляючого пристрою (регулятора), перетворювачі вибирають, виходячи з технологічних характеристик об’єкта. Природно, що ці елементи не підлягають зміні при корекції динамічних властивостей САУ. Незмінними,звичайно, також вважаються елементи, що забезпечують потрібну точність роботи системи в усталеному режимі –підсилювач, а в астатичній системі – інтегруючий елемент. Елементи САУ, що не змінюються, визначають ЛАЧХ вихідної не скоректованої системи. Бажану ЛАЧХ, яка визначає потрібну якість САУ, умовно поділяють на три частини: низькочасютну LНЧ(w), середньо частотну LСЧ(w) і високочастотну LВЧ(w). Можливий вигляд бажаної ЛАЧХ статичної системи показаний на рис.1.11. До низькочастотної частини ЛАЧХ належить ділянка характеристики, нахил якої не змінюється при w ® 0. Вона проходить через точку з координатами L(w)=20lg К,lgw=0, де К –коефіцієнт передачі розімкнутoї системи, і має нахил 0 дБ/дек для статичних систем, -20 дБ/дек – для астатичних систем першого порядку і -40 дБ/дек – для астатичних систем другого порядку. Низькочастотна частина ЛАЧХ визначається коефіцієнтом передачі розімкнутої системи K і порядком астатизму, отже, вона характеризує точність роботи системи в усталених режимах. Якщо до незмінюваної частини системи належать елементи, що забезпечують потрібну точність роботи САУ в усталеному режимі, то низькочастотні частини бажаної ЛАЧХ і ЛАЧХ вихідної системи збігаються. До середньо частотної частини належить ділянка ЛАХ з однаковим нахилом, що проходить через частоту зрізу wЗР. Ця частина ЛАЧХ є найважливішою, бо вона визначає переважно якість перехідних процесів. Основними параметрами, які характеризують середньо частотну частину, є її нахил і частота зрізу. Для задовільної якості перехідних процесів замкнутої системи необхідно, щоб нахил ЛАЧХ на частоті зрізу дорівнював -20 дБ/дек. Якщо нахил ЛАЧХ на частоті зрізу становить -40дБ/дек, то перехідний процес має велике перерегулювання, а при нахилі 60дБ/дек система, як правило, буде нестійкою. Частота зрізу wЗР визначає швидкодію САУ. Швидкодія зростає при збільшенні wЗР.
Рисунок 2.11 – Можливий вигляд бажаної ЛАЧХ статичної САУ Високочастотна частина ЛАЧХ LВЧ(w) знаходиться в зоні від'ємних децибелів, тому майже не впливає на якість перехідного процесу, а лише на його початок. Власне кажучи, краще мати якомога більший нахил асимптот високочастотної частини, бо це зменшує вплив високочастотних перешкод. У деяких випадках високочастотну частину ЛАХ взагалі не беруть до уваги. Для побудови бажаної ЛАЧХ, виходячи із заданих вимог до якості перехідних процесів, використовуються різні методи. Розглянемо найпоширеніші з них. Розглянемо метод В.В. Солодовнікова [3] стосовно астатичної системи першого порядку, в якої низькочастотні асимптоти з нахилом -20 дБ/дек вихідної LВ(w) бажаної ЛАЧХ LБ(w) збігаються і проходять через точку з координатами L(w)=20lg К,lgw=0 (рис 2.12). Вихідними даними для побудови бажаної ЛАЧХ є час регулювання tР і перерегулювання s%. Можуть бути заданими також максимальне прискорення а та початкове розузгодження вихідної координати х0. Бажану ЛАЧХ LБ(w) будують у такій послідовності. 1. Вибирають частоту зрізу, виходячи з умови: wЗР1 £ wЗР £ wЗР2, де wЗР1 – мінімальне значення частоти зрізу, при якому час регулювання не перевищує заданий; wЗР2 – максимальне значення частоти зрізу, яке визначають, виходячи із заданого максимального прискорення аmax регульованої координати та її початкового розузгодження х0.
Рисунок 2.12 – Побудова бажаної ЛАЧХ астатичної системи за методом В.В.Солодовнікова Значення wЗР1визначають за номограмою (рис. 2.11) у такому порядку. Виходячи із заданого значення s% за графіком s(Umax) визначають відповідне значення Umax. Потім за цим значенням (Umax) за графіком tР( Umax ) знаходять значення співвідношення сp/wЗР. Цю величину порівнюють із заданим значенням tР і із знайденого рівняння визначають: wЗР1=сp/ tР. Частоту wЗР2 обчислюють за формулою:
Якщо wЗР1 > wЗР2 то слід вибирати wЗР £ wЗР2. Якщо значення аmax і х0 не задані, то wЗР > wЗР1. 2. Після визначення частоти зрізу будують середньо частотну асимптоту бажаної ЛАЧХ, яка проходить через частоту зрізу з нахилом -20 дБ/дек. 3. На рисунку 2.13 зображений наближений графік номограми, за яким, виходячи із знайденого значення Umax, визначають LDj і Djmin. При виконанні розрахункової роботи слід скористатися довідниковим матеріалом, де наведені точні номограми, що дозволяють визначати координати середньо частотної ділянки асимптотичної бажаної ЛАЧХ скоректованої системи за заданими показниками якості перехідного процесу [ 6, 7].
Рисунок 2.13 – Графік номограми для визначення запасів стійкості скоректованої системи
Після побудови середньо частотної асимптоти бажаної ЛАЧХ, її сполучають з низькочастотною так, щоб в інтервалі частот, для якого: 0 £ LБ(w) £ LDj, (2.14) надлишок фази був більшим або дорівнював мінімальному надлишку: Δφ³ Δφmin. (2.15) Сполучення ЛАЧХ вихідної системи та середньо частотної ділянки бажаної ЛАЧХ здійснюють асимптотою з нахилом -40 дБ/дек або -60 дБ/дек для астатичних систем першого порядку і -60 дБ/дек – для астатичних систем другого порядку. Надлишок фази при частоті wможна визначити за такою наближеною формулою:
де ν— порядок астатизму; wi — частоти сполуки бажаної ЛАЧХ, які містяться ліворуч від wа; m і l — кількість частот сполуки, на яких нахил бажаної ЛАЧХ змінюється на -20 дБ/дек або +20 дБ/дек відповідно. Надлишок фази Δj = π + j(w),де j(w) < 0, перевіряють лише для тієї частоти wα(рис.1.12), для якої LБ(w) = LDj,. Частоті wαможе відповідати точка сполуки асимптот або точка на одній з цих асимптот. Задовольняння умов (2.14) і (2.15) означає, що бажаній ЛАЧХ відповідає типова частотна характеристика U(w), у якої |Umin| = Umax -1 і для якої складені використані раніше залежності s(Umax) і tp(Umax), наведені на рис... Якщо на частоті wαнадлишок фази Δja < Δjmin,то асимптоту сполуки необхідно зсунути вліво або зменшити її нахил; якщо Δja > Δjmin, то асимптоту слід зсунути вправо або збільшити її нахил. Отже, потрібне положення асимптоти сполуки відшукується методом спроб (ітерацій). При цьому різниця Δjа - Δjmin не повинна перевищувати кількох градусів. 4. Середньочастотну асимптоту сполучають з високочастотною так, щоб в інтервалі частот, для якого 0 ³ LБ(w) ³ LΔj, надлишок фази становив Δj ³ Δjmin. Надлишок фази досить перевірити при частоті ωб (рис. 2.12) за такою наближеною формулою:
де qсер– відносний нахил середньо частотної асимптоти (при нахилі -20 дБ/дек qсер =2); r – кількість частот сполуки бажаної ЛАЧХ, що перевищують частоту зрізу wЗР; wi– частоти сполуки бажаної ЛАЧХ, що перевищують wЗР. Якщо Δj < Δjmin, то асимптоту сполуки треба зсунути вправо або зменшити її нахил, якщо Δj > Δjmin, то необхідно цю асимптотузсунути вліво або збільшити нахил. Різниця Δj - Δjmin не повинна перевищувати кількох градусів. При сполученні середньо частотної частини ЛАЧХ з низькочастотною та високочастотною слід прагнути до того, щоб бажана ЛАЧХ якомога менше відрізнялась від ЛАЧХ вихідної системи. Це спрощує корекцію та подальшу технічну реалізацію коректуючого пристрою. Синтез послідовного коректуючого пристрою здійснюють також із застосуванням метода Санковського-Сігалова [4, 7]. В основу цього методу покладено дев'ять типів бажаних ЛАЧХ розімкнутої системи (табл. 2.1). Той чи інший тип ЛАЧХ вибирається залежно від вимог до САУ, яка синтезується. Ці вимоги є вихідними даними для синтезу. До них належать: (dg/dt)max, (d2g/dt2)max– максимальне значення швидкості та прискорення зміни завдання; t – час регулювання; σ% – перерегулювання. При виборі типу ЛАЧХ рекомендується керуватися такими положеннями: 1) якщо завдання змінюється з великим прискоренням, а рівень перешкод незначний, то слід вибирати ЛАЧХ типу 1 для статичних систем 2) якщо прискорення, з яким змінюється завдання, невелике, але рівень 3) при великих прискореннях зміни завдання і значному рівні перешкод треба вибирати ЛАЧХ типів 6, 7, 8 або 9. У всіх випадках при виборі бажаної ЛАЧХ слід прагнути до того, щоб бажана ЛАЧХ якомога менше відрізнялася від ЛАЧХ вихідної системи. Після того як тип бажаної ЛАЧХ вибрано і, виходячи з вимог до якості САУ в усталеному режимі, визначено її низькочастотну частину, для побудови решти частин бажаної ЛАЧХ використовують дані таблиці 2.1 і такі співвідношення: частота зрізу: w3 = c/tр, (2.18) запас стійкості по фазі: Dj° = 73 - σ, (2.19) де c=9 при Dj° = 30 °; c=8 при Dj° = 45 ° і c=7 при Dj° = 60 °. Формули (2.18) і (2.19) дають похибку, що не перевищує 0,05... 0,1% при 60 ° > Dj° > 30 °. При розрахунках можна користуватися й такими співвідношеннями:
де l= 2 або 3 при нахилі асимптоти, що сполучає середньо- та низькочастотні частини ЛАЧХ, -40 дБ/дек або -60 дБ/дек; а = π/2 - Dj°. Значення а (у радіанах) визначають, виходячи з припущення, що wЗР/wi << 1 при і = 3, 4,... wЗР/w1 >> 1. Спрощена побудова бажаної ЛАЧХ [3]. Вихідними даними для побудови Lб(w) є час регулювання tрта перерегулювання s%.Частота зрізу бажаної ЛАЧХ обчислюється за формулою: wЗР»k0p/tp, де k – коефіцієнт, що визначається за графіком на рис. 2.14,aзалежно від перерегулювання s%.
Таблиця 2.1 – Основні типи бажаних ЛАЧХ
а б
в Рисунок 2.14 – Номограми для спрощеної побудови бажаної ЛАЧХ скоректованої системи
Через частоту зрізу wЗРпроводиться середньо частотна асимптота бажаної ЛАЧХ з нахилом -20 дБ/дек. Частоти w2і w3, що обмежують ceредньочастотну асимптоту ліворуч і праворуч, вибирають, виходячи з таких наближених рівностей:
Для наближеної, але досить точної оцінки показників якості перехідного процесу можна використати графіки на рисунку 2.14. Перерегулювання σ визначається за графіками на рисунку 2.14,бзалежно від коефіцієнтів а2 і a3,що визначають довжину середньо частотної частини ЛАЧХ: а2=w2/wЗР, а3=w3/wЗР. Запас стійкості по фазі Δj0 визначається за графіком на рисунку 2.14,в залежно від перерегулювання s%. Наведемо скорочено послідовність процедури синтезу САУ за допомогою діаграм Солодовнікова, які встановлюють зв'язок між перерегулюванням s%, часом перехідного процесу tпп, wЗ -частотою зрізу системи, тобто тією частотою, де коефіцієнт передачі системи дорівнює 1 або L(w) = 0, і величиноювідношення Рмах/ Р0. При синтезі послідовного коректуючого пристрою використовується поняття області суттєвих частот. Область суттєвих частот Якщо, наприклад, розглядати логарифмічну частотну характеристику (ЛАЧХ) розімкнутої системи на інтервалі
а б Рисунок 2.15 – Можливий вигляд дійсної частотної характеристики (а); Номограми визначення частоти зрізу бажаної ЛАЧХ скоректованої системи згідно заданих показників якості перехідної характеристики (б)
За графіком номограми, наведеної на рисунку 2.15,б, можна, наприклад, визначити при заданому перерегулюванні s% і часі перехідного процесу tпп частоту зрізу системи. Загальний алгоритм синтезу САУ може бути, наприклад, таким. Послідовна коректуюча ланка вводиться в основний контур регулювання системи і звичайно є пасивним чотириполюсником або регулятором на базі операційного підсилювача. По можливості ланку слід вводити ближче до входу системи, де сигнали мають найменшу потужність. Далі необхідно виконати наступні дії: 1. Заданіпоказники якості перехідної характеристики бажаної системи: перерегулювання s% у відсоткахтачас перехідного процесу tпп (с). Виходячи із заданої структури системи і параметрів її ланок, будують ЛАЧХ вихідної розімкнутої системи LВ(w); 2. За заданими показниками якості будують бажану ЛАЧХ LБ(w). Для цього по діаграмах (рисунок 2.10,б або 2.14,а) визначаютьчастоту зрізу wз. Будують область суттєвих частот, що дає нам основну середньо частотну частину бажаної ЛАЧХ. Добудовують ВЧ частина довільно і НЧ частина, виходячи з необхідного порядку астатизму. 3. Визначають ЛАЧХ коректуючої ланки LК(w) як різницю LБ(w)-LВ(w). За ЛАЧХ коректуючої ланки LК(w) визначають її передаточну
Завдання до роботи. 5.1. Вибір завдання. Завдання вибирається наступним чином: номер варіанта повинен співпадати з останньою цифрою номера залікової книжки студента; номер підваріанта – з передостанньою цифрою номера n, якщо вона не перевищує 5, та визначається n-5, при n>5. Якщо передостання цифра шифру 0, то n прирівнюється до 10. Завдання. По даних функціях передачі окремих елементів (дивись відповідний варіант та таблицю) системи, структура якої зображена на рисунку необхідно: - провести дослідження нескоректованої системи на стійкість за допомогою вказаного в таблиці критерію; - побудувати ЛАЧХ та ЛФЧХ нескоректованої системи і підтвердити висновок щодо її стійкості; - провести послідовну корекцію структури початкової системи, з метою досягнення заданих часу перехідного процесу tПП і перерегулювання s% (дивись таблицю), знайти перехідну характеристику системи, визначити параметри якості регулювання та запаси стійкості системи по амплітуді та фазі; - знайти ЛАЧХ послідовної коректуючої ланки, визначити електричну схему та розрахувати її параметри; - симулювати електричну схему у ППП Micro-Cap або Electronic WorkBench 5.x. Нижче приведені: структурна схема (рис. 5.1) системи, вигляд функцій передачі окремих типових динамічних ланок замкнутої системи для варіантів 0…9 завдання (таблиця 5.1), а також таблиця значень параметрів цих елементів, показників якості перехідного процесу з вказаним критерєм стійкості, який має бути застосований при дослідженні динамічних властивостей САУ.
Рисунок 5.1 – Структурна схема системи
Таблиця 5.1 – Функції передачі замкнутої САУ
Таблиця 5.2 – Параметри елементів САУ та її показники якості
При дослідженні стійкості за допомогою різних критеріїв слід пам’ятати, що частина з них відноситься до розімкнутих систем, а інші – до замкнутих. Крім того, треба звернути увагу на відповідну нумерацію коефіцієнтів характеристичного рівняння. При побудові ЛАЧХ і ЛФЧХ треба спочатку побудувати характеристики елементарних ланок, а потім шляхом сумування знайти характеристики систем в цілому. При цьому треба використовувати логарифмічний (ЛАЧХ) та напівлогарифмічний (ЛФЧХ) масштаб. Корекція системи за допомогою послідовної коректуючої ланки є найбільш складним етапом роботи. Ітераційний процес корекції на кожному кроці містить: - побудову бажаної ЛАЧХ, яка здійснюється на основі попередніх знань про зв’язок параметрів цієї ЛАЧХ із варіаціями перехідної характеристики та параметрів якості перехідного процесу; - побудову перехідної функції системи, яка відповідає бажаній ЛАЧХ, за допомогою ПЕОМ; - визначення параметрів tПП і σ% та порівняння їх з вихідним технічним завданням; - завершення процедури або перехід до наступного ітераційного кроку, якщо знайдені параметри не відповідають технічному завданню. ЛАЧХ коректуючої ланки знаходиться як різниця двох ЛАЧХ – після введення і до введення корекції. Після цього за відповідними таблицями визначають її схему і параметри. До пояснювальної записки слід обов’язково включити: - структурну схему системи із позначеннями на ній коректуючої ланки; - ЛАЧХ і ЛФЧХ нескоректованої системи; - бажану ЛАЧХ та перехідну характеристику системи для трьох останніх ітерацій; - принципову електричну схему коректуючої ланки з позначеними на ній узгодженими елементами; - опис та листінги розроблених програм для ПЕОМ, результати розрахунків, знайдені за допомогою цих програм, а також порядок використання та результати роботи з програмами, що були розроблені раніше. Всі розрахунки і необхідні графічні матеріали доцільно виконати у середовищі MatLab 6.0, коректуючих ланок – за допомогою ППП MicroCap або Electronic WorkBench 5.x. Необхідно звернути особливу увагу на правильність вико
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.60 (0.011 с.) |

 :
: . (2.12)
. (2.12) ; при
; при  .
.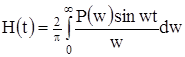 . (2.13)
. (2.13)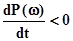 ).
).









 (2.16)
(2.16) (2.17)
(2.17)



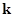


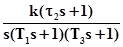




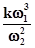


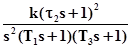
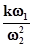



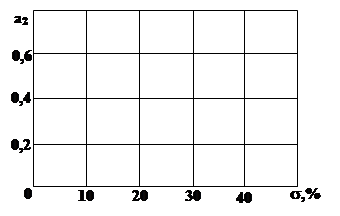

 – це та частина частотної характеристики, яка в основному визначає якість процесів регулювання у системі управління. Тобто поведінка ДЧХ поза цією областю вже не робить помітного впливу на показники якості перехідного процесу.
– це та частина частотної характеристики, яка в основному визначає якість процесів регулювання у системі управління. Тобто поведінка ДЧХ поза цією областю вже не робить помітного впливу на показники якості перехідного процесу. , тоді коефіцієнт передачі САУ Кпер визначається виразом 20log(Кпер)=26Дб Þ Кпер»20, звідки можна визначити величину усталеної похибки:
, тоді коефіцієнт передачі САУ Кпер визначається виразом 20log(Кпер)=26Дб Þ Кпер»20, звідки можна визначити величину усталеної похибки:
 тобто нижня частота суттєвих частот визначається статичною точністю САУ
тобто нижня частота суттєвих частот визначається статичною точністю САУ 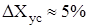 і повинна бути розташована лівіше частоти
і повинна бути розташована лівіше частоти  ЛАЧХ не нижче +26дб, якщо система не повинна володіти астатизмом, або має нахил у залежності від порядку астатизму.
ЛАЧХ не нижче +26дб, якщо система не повинна володіти астатизмом, або має нахил у залежності від порядку астатизму.