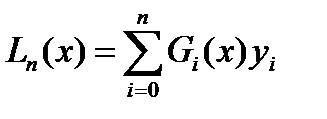Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация ппо. Табличная организация информации. Табличные модели. Табличные процессоры.Содержание книги
Поиск на нашем сайте
ППО: универсальн. и специализир-ое. УППО: сис-мы обр-ки текстов, ср-ва машин. графики, СУБД, ср-ва обр-ки эл-ных таб., интегрир. пакеты. Эти прог.ср-ва не привязаны к к.-л. предм. обл-ти.=> возм-ть исп-ть их в разл. обл-тях. Особ-ти разраб-ки- отсут-ие конкр. заказчика. УППО д\б мобильным, легко адаптируемым к разл. моделям ЭВМ, просты в освоен. и эксплуат-и. СППО: расчит. на конкр. группу польз-лей, тесно связ с опред. предм. обл-ю; оно д/б надежным, корректным, соотв-ть спец-ке условий экспл-ции. Тираж-ие возм-но, но в значит. меньших масштабах.Кним относ-ся: сис-мы автомат-го проект-ия, банковские фин. сис-мы, сист. управл-ия произв-вом, бух. учета, эксперт. сис-мы д/ конкр. зад., мат. пакеты и др. Выд-ют еще уникальное ППО- разраб. по инд.. заказу, исп-ся для науч. и инж.. расчетов, созд сис-мы иск. ител-та. Табличный процессор, — категория программного обеспечения, предназначенного для работы с электронными таблицами. Изначально табличные редакторы позволяли обрабатывать исключительно двухмерные таблицы, прежде всего с числовыми данными, но затем появились продукты, обладавшие помимо этого возможностью включать текстовые, графические и другие мультимедийные элементы. Инструментарий электронных таблиц включает мощные математические функции, позволяющие вести сложные статистические, финансовые и прочие расчеты. Под электронными таблицами будем понимать ПС обработки крупноформатных электронных динамических таблиц. Средства данного типа обрабатывают таблицы, состоящие из строк и столбцов, на пересечении которых располагаются клетки. Каждая клетка такой таблицы может содержать числовое значение, формулу или текст. Клетки идентифицируются именами, состоящими из номера строки и номера столбца, например, A55,G50,S3 и т.д. Значение в числовой клетке таблицы может быть записано или вычислено по ассоциируемой с данной клеткой формуле; в формуле могут присутствовать ссылки на другие клетки таблицы. Каждый раз при изменении значения в клетке таблицы в результате записи в нее нового значения с консоли ЭВМ, перевычисляются и значения всех тех клеток, которые содержат величины, зависящие от изменяемой клетки. Возможность запоминания текста в привязке к клеткам таблицы используется для присваивания заголовков столбцам, названий строкам и т.д. Электронные таблицы, в частности, весьма удобны для реализации на ПК, поддерживающих режим быстрого и гибкого манипулирования цветными изображениями на экране монитора. Общей характерной чертой всех электронных таблиц является использование экрана в качестве окна обзора таблицы целиком либо по выбранным ее участкам; если число строк и столбцов слишком велико, то окно обзора можно перемещать по таблице по горизонтали и вертикали, обозревая ее невидимые части. Для изменения какого-либо значения достаточно поместить курсор в соответствующую клетку таблицы, визуализируемую на экране, и записать с консоли в нее новое значение. При этом, обеспечиваются хранение в памяти ПК и просмотр на экране монитора таблиц большой размерности; размещение крупных работ (макросов), содержащих ссылки на другие клетки документа и встроенные функции; отображение на экране значений, вычисляемых по формулам, хранящимся в клетках документа; автоматическая корректировка результатов документа при изменениях содержимого клеток, на которые в формулах имеются ссылки; графическое отображение информации и т.д. Электронные таблицы оказываются весьма эффективным способом обработки различного рода информации, которую можно представлять в табличной форме (научная, деловая, коммерческая и т.д.). Среди средств данного типа наиболее известными и популярными являются пакеты Lotus 1-2-3, Quattro Pro [17,18], SuperCalc и Ms Excel Табличные модели. Одним из наиболее часто используемых типов информационных моделей является таблица, которая состоит из строк и столбцов. С помощью таблиц создаются информационные модели в различных предметных областях. Широко известно табличное представление математических функций, статистических данных, расписаний поездов и самолетов, уроков и т. д.Табличные информационные модели проще всего формировать и исследовать на компьютере посредством электронных таблиц и систем управления базами данных.
Пусть некот. ф-ция задана таблично (n+1) знач.: (x0,y0),(x1,y1),…,(xn,yn). Треб-ся найти ф-лу f(x) такую, что yi=f(xi), где i=0,n. В данной постан-ке з-ча неопред., т.к. реш. неединс-но. Для единст-ти реш., выбир. конкрет. класс ф-ций (показат., log, и т.д.). Чаще всего реш. ищут в классе многочлен. и формулир. з-чу т.о.: по (n+1)-точке построить многочлен n-ой степ. y=Pn(x) такой, что yi=Pn(xi). Процесс нахожд. реш. наз. интерполив-ем, ф-ция интерпол-ной, h=xi-xi-1-шагом инт-ия точки yi,xi-узлами интер-ния. Если строится многоч., говорят о параболич. интерпол-нии. Если h=const для i=0,n – узлы наз-ют равноотстоящими. I. Интер-ный многочлен Ньютона для ф-ий с равноотс. узлами. Пусть даны (n+1)-точка и причем. xi+1=xi+h=x0+ih; для i=0,n. Построим многоч. n-ой степ.т/что Pn(xi)=yi. Реш. б/м искать в виде: Pn(x)=a0+a1(x-x0)+…+an(x-x0)(x-x1)…(x-xn-1). Найд. коэф-ты ai, i=0,n; для этого б/м подст-ть посл0но в выражен. вместо x знач. x0,x1,…,xn. Положим x=x0 => a0=y0, положим x=x1 => a1=(y1-y0)/h=Δy0/h, положим x=x2 => a2=Δ2y0/2h2 и т.д. Т.О.: Наз. ф-лой интерпол-ния вперед (пригодна для вычисл. точек, лежащ. в нач. таблицы). Для вычис знач. в точках, лежащ. в конце таблицы использ. 2-ой интерпол-ый многоч. или ф-лу интерпол-ия назад: II. Интерпол-ый многоч. Лагранжа для ф-ций с неравноотст. узлами. Введ. вспомог. ф-ию: Рассм-м сумму: нетрудно видеть, что Ln(x)-многоч. n-ой степ., причем Ln(xi)=yi, т.е. Ln(x) есть интерпол-ный многоч. наз. многоч. Лагранжа.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

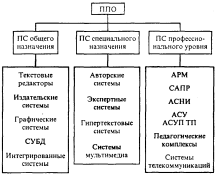 ППО - это часть ПО, пред-ная д/ того, чт. обеспечить примен-ие ВТ в разл. сферы деят-ти ч-ка. Стр-ра и прин-п постр-ия ПП зависит от ЭВМ и ОС, в рамках кот. она будет функц-ть. ПП реал-ся на конкр языке прог-ия.Внаст. время предл-ся разл. ППП, автомат-щие сферы чел. деят-ти (редакторы, эл. таб, банки дан., информ-но – поисковые сис-мы, мат. прог-мы, эксперт. сис-мы).
ППО - это часть ПО, пред-ная д/ того, чт. обеспечить примен-ие ВТ в разл. сферы деят-ти ч-ка. Стр-ра и прин-п постр-ия ПП зависит от ЭВМ и ОС, в рамках кот. она будет функц-ть. ПП реал-ся на конкр языке прог-ия.Внаст. время предл-ся разл. ППП, автомат-щие сферы чел. деят-ти (редакторы, эл. таб, банки дан., информ-но – поисковые сис-мы, мат. прог-мы, эксперт. сис-мы).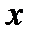
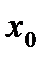

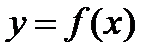 22.Постановка задачи интерполирования. Формулы параболического интерполирования. Сплайны.
22.Постановка задачи интерполирования. Формулы параболического интерполирования. Сплайны.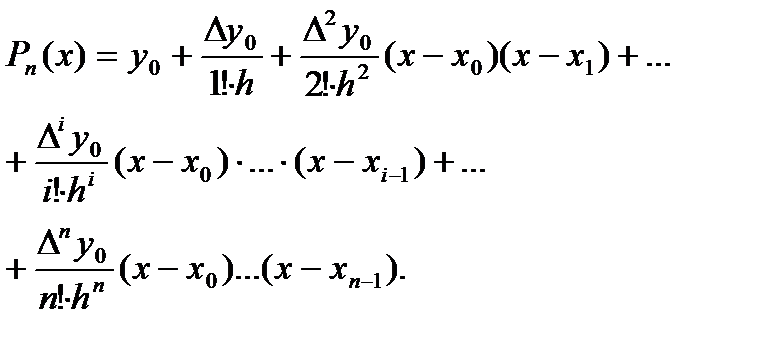
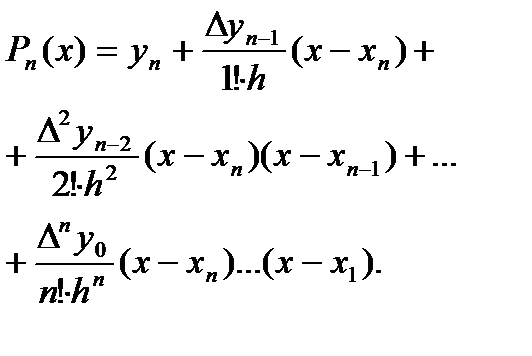
 Gi(x)-есть многочлен n-ой степ., причем
Gi(x)-есть многочлен n-ой степ., причем