
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информация. Виды и свойства информации. Информационные процессы и технологии. Общие принципы кодирования информации и формы ее представления В эвм.Содержание книги
Поиск на нашем сайте СОДЕРЖАНИЕ 1. Информация. Виды и свойства информации. Информационные процессы и технологии. Общие принципы кодирования информации и формы ее представления в ЭВМ. 2 2. Моделирование стохастических систем. Моделирование случайных величин с равномерным распределением. Методы проверки случайности данных. Моделирование случайных величин с заданным распределением. 4 3.Методы приближенного решения дифференциальных уравнений. Погрешность методов. 6 4. ЯП пролог и логическое программирование. Структура программ. Особенности исполнения. 7 5. Основы понятия "алгоритм". Алгоритм: содержательный и формализованный подходы к понятию "алгоритм". Свойства алгоритма и способы его описания. 8 6. Граф. Вершины и ребра графа. Виды графов. Пути. Связность, мосты и точки сочленения. Компоненты связности. Двудольный граф. Способы задания графа. 9 7. ЭВМ как средство обработки информации. Классификация ЭВМ. Перспективы развития вычислительной техники. 10 8. Основы анализа алгоритмов. Асимптотическая временная сложность алгоритмов. Классификация скоростей роста сложности алгоритма. О-символика. 11 9. Машина Тьюринга. Операции над машинами Тьюринга. Вычислимость по Тьюрингу частично-рекурсивных функций. Совпадение класса всех нормально вычислимых функций с классом функций вычислимых по Тьюрингу. 12 10. Элементы теории игр. Понятие об игровых моделях. Нижняя и верхняя цены игры. Принцип минимакса. Вполне определенные игры, не содержащие седловой точки. Решение игр в смешанных стратегиях. Геометрическая интерпретация игры 2x2. 13 11. Нейр. сети. Одн. перцептр. Актив. ф-ия. Лог. операц. на основе прст. перцептр. 15 12. Приближенное решение уравнений. Методы бисекции, хорд, касательных, комбинированный, итераций. Погрешность методов. 15 13. Виды компьютерной памяти. Устройства памяти, принципы их рабты и характеристики. 17 14. Классификация ППО. Программы создания рисунков. Методы представления графических изображений. Растровая и векторная графика. Системы цветов в компьютерной графике. Форматы графических файлов. 18 15. Принципы функционирования локальных вычислительных сетей. Устройства поддержки работы ЛВС. Типы ЛВС. Одноранговые сети. Сети на основе сервера. Комбинированные сети. 19 16. Моделирование стохастических систем. Общая схема метода Монте-Карло. Особенности моделирования систем массового обслуживания. Математическая модель систем массового обслуживания. 21 17. Элементы теории двойственности. Прямая и двойственная задачи линейного программирования. Основные теоремы двойственности. Применение двойственного симплексного метода. 22 18. Основные типы кабельных сред передачи данных. Узкополосная и широкополосная передача сигналов. Асинхронная передача и автоподстройка. Сетевой адаптер. Беспроводные сети. Передача "точка-точка". Инфракрасные лазерные ЛВС. Беспроводные ЛВС с радиопередачей. 23 19. Геометрическое моделирование. Представление геометрических объектов (точка, прямая, линия, плоскость, поверхность, фигура). Представление геометрических преобразований плоскости и пространства. Алгоритмы построения линий и поверхностей. 26 20. Алгебра высказываний. Нормальные формы. Совершенные нормальные формы. Теорема существования нормальной формы. Приложение алгебры высказываний к логико-математической практике. 27 21. Классификация ППО. Табличная организация информации. Табличные модели. Табличные процессоры. 28 22.Постановка задачи интерполирования. Формулы параболического интерполирования. Сплайны. 29 23. Понятие типа данных. Простые (базовые) типы данных. Ссылочный тип. Структурированные типы данных (массивы, записи, множества, файлы). Переменные. Область видимости переменных. 30 24. Теория рекурсивных функций. Классы вычислимых функций. Примитивно рекурсивные операции. 32 25. Линейность, ветвление и цикл. Их реализация в языках программирования и обобщения. Подпрограммы. Реализация подпрограмм в языках программирования. Рекурсия. Модульное программирование. 33 Информация. Виды и свойства информации. Информационные процессы и технологии. Общие принципы кодирования информации и формы ее представления в ЭВМ. Пон-ие инф-ии явля-ся фунд. пон-ем в любой науке вообще и базовым в И. Формаль-го опр-ия не имеет. Каждая наука рассм. это понятие со своей стороны. В филос-ии под инф-ей понимают отражение реального мира. Инф. м/о классиф-ть по: форме, структуре, способу передачи и восприятия (обмену), области возникновения. С пон-ем инф-ии связаны след-ие пон-ия: 1) Сигнал - представл-ий собой любой физ. процесс, несущий инф-ию. 2) Сообщение - инф-ия, представл-ая в опред-ой форме и предназ-ая для передачи. 3) Данные - инф-ия, представл. в формализованном виде и подготовленная для обраб-ки технич-и устр-ми. Инф-ия может перед-ся сигналами 2-ух типов: непрер-ый (парам-ры сигнала м. принимать любые зн-ияиз данного диапазона); дискретный (пар-ры сигнала приним-ют конечное число знач-ий из данного диапазона). Инф-ия, предст-ая в любой форме, - это отражение окр-го нас мира с помощью знаков и сигналов. Отражение д/но быть правдивым и не искажать оригинала, а для этого она д/на обладать такими необх-ми св-ми как достоверность и полнота, ценность и актуальность, ясность и понятность. Ед. измер. инф-ии. Сущ. 2 подхода: вер-ый и объемный. 1) Кол-вом инф-ии наз-ют числ. хар-ку сигнала, отраж-ую ту степень неопр-сти, кот. исчезает после пол-ия сигнала. Под единицей инф-ии понимают такое ее кол-во, кот. уменьшает неопредел-сть в 2 раза. Ед-ца изм. инф. - бит. N - кол-во событий, i - кол-во инф-ии N=2i; I=log2N.Если кол-во равновер-ых соб-ий = N, то кол-во инф-ии i, полученное при выпадении этого соб-ия, м/б выч-но по фор-ле Хартли i=log2N. За ед-цу инф-ии в сист. СИ принимают 1 байт=8 бит. 2) Объем инф-ии в памяти ЭВМ или на носителе равен кол-ву бит. ИП. Действия выпол-е с инф-ей наз инф. процеессами. К ИП относят сбор, обраб-ку, хранение и обмен инф-ей. Сбор инф-ии - деят-сть, в ходе кот. пол-ют сведения об интересующем объекте. М. осущ-ся как чел-ком, так и аппаратно. Обработка – упорядоченный процесс ее преоб-ия в соотв-ии с нек-ым алгоритмом. Хранение – процесс поддержания инф-ии в виде обеспечивающем выдаче конечных данных по запросам пользователей в установл-ые сроки. Обмен - процесс, имеющий две формы: передача, прием. Обяз-но присутств-ют источник и приемник инф-ии и среда передачи инф-ии. Матер-ый носитель - сигнал. (пример сх. Шеннона). ИТ - процессы, испол-ие сов-сть ср-в и м-дов для обеспечения ИП: сбора, обраб-ки и передачи данных (первичной инф-ии), для пол-ия инф-ии нового кач-ва о сост-ии объекта, процесса или явл-ия (инф. продукта). Цель ИТ - произ-во инф-ии для ее анализа чел-ком и принятия на его основе реш-ия по вып-ию к-л действия. Внедрение ПК в инф-ую сферу и прим-ие телекоммуникаций опред-ли новый этап раз. инф. технологий. НИТ - ИТ с «дружественным» интерфейсом р-та пользователя, исп-ая ПК и телекомм-ые ср-ва. Общая идея симплекс метода и ее реализация в таблице Чаще всего реализацию симпл.метода сводят к следующему: на нач. этапе систему ограничений, т.е.д/б выделен базис, базисное реш-е не должно быть отрицательным или что равносильно все правые части должны быть не отрицат. числами. Из ЦФ должны/б исключены основные или базисные переменные. Удобно для преобр. Сист использ.шаги жардано-гаусса. погрешность метода Когда задача в точной постановке не решается, ее заменяют близкой по результатам приближенной задачей. Выбор более сложно решаемой задачи иногда позволяет уменьшить погрешность ценой возрастания объема вычислений; Машина Тьюринга. Операции над машинами Тьюринга. Вычислимость по Тьюрингу частично-рекурсивных функций. Совпадение класса всех нормально вычислимых функций с классом функций вычислимых по Тьюрингу. Машина Тьюринга есть математическая(воображаемая) машина, а не машина физическая. Она есть такой же математический объект, как функция, производная, интеграл, группа и т.д. И так же как и другие математические понятия, понятие машины Тьюринга отражает объективную реальность, моделирует некие реальные процессы. Элементы теории игр. Понятие об игровых моделях. Нижняя и верхняя цены игры. Принцип минимакса. Вполне определенные игры, не содержащие седловой точки. Решение игр в смешанных стратегиях. Геометрическая интерпретация игры 2x2. Математические методы анализа конфликтных ситуаций объединяются под названием теории игр, сама конфликтная ситуация носит название игры, а стороны, участвующие в конфликте, называются игроками. Исход игры называется выигрышем (или проигрышем) игроков. Если в игре участвуют только два игрока, то игра называется парной. Будем рассматривать в дальнейшем только парные игры. Если выигрыш одного игрока равен проигрышу другого, то игра называется антагонистической. Величина a называется нижней ценой игры или максимином. Это гарантированный выигрыш игрока А. С другой стороны, игрок В выбирая свою стратегию В j понимает, что игрок А ответит такой стратегией Аi, чтобы его выигрыш был максимален. Поэтому из наилучших вариантов для А (максимальных элементов каждого столбца) Величина β называется верхней ценой игры или минимаксом. Это максимальный проигрыш игрока В. Реальный результат решения конфликтной ситуации, называемый ценой игры n, заключен между верхней и нижней ценой: Вполне определенные игры называют играми с седловой точкой. Элемент Смешанной стратегией SA игрока А называется применение чистых стратегий A1, A2,..., Am с вероятностями p1, p2,..., pi,..., pm причем сумма вероятностей равна 1: или в виде строки SA = (p1, p2,..., pi,..., pm) Аналогично смешанные стратегии игрока В обозначаются: Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение (или решение) игры: это пара оптимальных стратегий S*A, S*B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству: α ≤ v ≤ β, где α и β — нижняя и верхняя цены игры. Решение игры 2×2 допускает наглядную геометрическую интерпретацию. Пусть игра задана платежной матрицей Р = (aij), i, j = 1, 2. По оси абсцисс (рис. 3.1) отложим единичный отрезок A1 A2 точка A1(х=0) изображает стратегию A1, а все промежуточные точки этого отрезка — смешанные стратегии SA первого игрока, причем расстояние от SA до правого конца отрезка — это вероятность p1 стратегии A1, расстояние до левого конца — вероятность p2 стратегии A2. На перпендикулярных осях I — I и II — II откладываем выигрыши при стратегиях A1 и A2 соответственно. Если 2 -й игрок примет стратегию B1, то она дает выигрыши a11 и a21 на осях I — I и II — II, соответствующие стратегиям A1 и A2. Обозначим эти точки на осях I—I и II—II буквой B1. Средний выигрыш v1, соответствующий смешанной стратегии SA, определяется по формуле математического ожидания v1 = a11 p1 + a21 p2 и равен ординате точки M1, которая лежит на отрезке B1 B1 и имеет абсциссу SA (рис. 3.1).
Аналогично строим отрезок B2B2, соответствующий применению вторым игроком стратегии B2 (Рис. 3.2). При этом средний выигрыш v2 = a12 p1 + a22 p2 — ордината точки M2. В соответствии с принципом минимакса оптимальная стратегия S*A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 3.3 в примере 3.4.1), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B1 N — против стратегии B1 , на участке NB2 — против стратегии B2). Оптимальную стратегию S*A = (p*1 , p*2) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v. На рис. 3.3 (пример 3.4.1) обозначены также верхняя и нижняя цены игры α и β. Метод бисекций. Пусть дано ур-ие f(x)=0 где f(x)-непрерывно на некотором конеч или бесконеч интерв. Конем этого ур. Назовем " число обращ-е f(x) в 0, если f(x0)=f /(x0)=…fk-1(x0)=0, то x0 корень кратности к точно решить данное ур-ие не всегда удается, будем гов-ть, что x—есть приближенное решение ур-ия с точн-ю e если |a-x––| <=e,где а точный корень –e<= a-x––<=e или a-e<=x––<=a+e.Задача о нахожд приближ корня обычно реш-ся в 2 этапа 1) отдел-ся корень т.е. ищется по возм-ти небольш отр-ок [a, b] содерж ровно один корень. 2) корень уточн-ся до нужной точности. 1) а) отделение корня м.о. пр-ти графически. б) если график сложен, то ур-е мо переписать в виде g(x) =f(x) (и построить гр-ки y=g(x), y=f(x) и точка пересеч б.т. корень). в) мо для отделен корня исп-ть. теор. Т.если непрерыв ф-я на концах отр приним-ет значен разных знаков, то на отр-ке она имеет по кр-не. мере один корень. Если ф-я монотонна, то кор-нь один. Пусть изв-но, что корни Ур-я нах-ся на конц отр-ка [a,b]разделим отрезок на равные части точками a=a0<a1<…<an=b и проверим знаки на концах отр-ка [ai,ai+1] i=0,n-1 если условие теор вып-ся отр-к содерж корень, алгор-м метода м.б. следующим а,в концы отрезка, n-кол-во отр-ов деления.
2) одним из простейших способов уточнения корня явл-ся метод бисекции сост-ий в следующем: пусть на отр. [a,b] yf[-cz ровно 1 корень уровн. Найдем корень с точн-ю e. Разделим отр. Пополам. Точкой x1 =(a+b)/2, половину содерж корень вновь делим пополам итд. Процесс прекращ, когда длина отр-ка не станет <=2e тогда за приближ значение корня x–– возьмем середину этого отр-ка. Алгоритм следующий.
Теорема явл-ся достаточной но не обязат для сходимости. Геометрич смысл метода итераций.
Алгоритм имеет вид Методами хорд и касс-ых. М-д хорд.
Пусть корень Ур-ния f(x)=0, [a,b] допустим, что на [a,b] существ. f’’(x), к-ое не мен. знак. Пусть для определ-ти f(a)<0. Пусть f’’>0 (рис.): провед. хорду АВ и найдем ее пересеч. с осью x. Пусть А1 пересечение y=f(x) и прямой x=x1, проводим хорду А1В, пусть x2 – ее пересеч. с осью x и т.д. Получ. ∞ числов. послед-ть {xn}. Для нахожд. xi используем Ур-ние прямой, прох. ч/з 2 точки:
В послед-сти xn: a=x0<x1<…<xn<…<b т.е. посл-ть xn имеет предел, как возрост-ая и ограниченная сверху, т.е. перейдя к пределу:
М-д касательных. Пусть корень ур-ния f(x)=0 отделен на отрез. [a,b], причем f’’ не меняет знака на [a,b]. Возьмем для опред-сти f(a)<a, f’’>0
Провед. касат. к тому концу дуги АВ в к-ром f*f’’>0. Пусть x1 ее пересеч. с Ox обозначим ч/з b1 пересеч. прямой x=x1 и дуги АВ. Провед. касат. в т.В1 пусть x2 ее пересеч. с Ox и т.д. Получ. ∞ послед-ть {xn} имеющую предел как убывающая и огранич. xn – б/м искать из ур-ния касат. Ищем x1: y-f(b)=f’(b)(x-b), полагая y=0 x=x1
т.к.
На практике для получ. корня с точн. ε заканчив. вычисл., когда Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики. Применение Трудность установки кабеля — фактор, который дает беспроводной среде неоспоримое преимущество. Она может оказаться особенно полезной в следующих ситуациях: в помещениях, заполненных людьми (например, в прихожей или приемной); для людей, которые не работают на одном месте (например, для врачей или медсестер; в изолированных помещениях и зданиях; в помещениях, планировка которых часто меняется; в строениях (например, памятниках истории или архитектуры), где прокладывать кабель непозволительно. Типы беспроводных сетей В зависимости от технологии беспроводные сети можно разделить на три типа: локальные вычислительные сети; расширенные локальные вычислительные сети; мобильные сети (переносные компьютеры). Промежуточным этапом от кабельных сетей к беспроводным является способ передачи «точка-точка». Трансивер-устройство для подключения компьютера к сети, т.е. устройство устанавливающее прием и передачу сигнала. ПЕРЕДАЧА «ТОЧКА-ТОЧКА». Позволяет передавать сигналы между двумя компьютерами или между компьютером и другим устройством (принтер,сканер). Трансивер для беспроводной передачи данных иногда называют точкой доступа. В беспроводных сетях чаще всего используют переносные или настенные трансиверы. Они устанавливают радиоконтакт между переносными устройствами. Однако такую сеть нельзя назвать полностью беспроводной из-за подключения трансиверов. Технология тока точка основана на последовательной передаче данных и обеспечивает высокоскоростную и безошибочную передачу данных применяя радиоканал точка точка а также проникновении сигнала через стены и перекрытия. МОБИЛЬНЫЕ СЕТИ. В беспроводных мобильных сетях в качестве среды передачи выступают мобильные телефонные системы и общественные службы. Существует 3 способа организации таких сетей: - на пакетном радиосоединении; - сотовые сети; - микроволновые системы. Имея при себе переносной компьютер при помощи мобильных сетей возможно обмениваться файлами, электронной почтой и др.информацией, но такая система довольно медленна. Скорость передачи данных от 8 до 34 Кбит/с. Для подключения такого способа передачи данных используют сетевые адаптеры использующие технологию сотовой связи. Небольшие антенны переносных ПК связывают их с окружающими радиотрансляторами. При пакетном радиосоединении данные разбиваются на пакеты в которых содержатся: имя отправителя, имя получателя, информация для коррекции ошибок и сами данные. Пакеты отправляются на спутник и со спутника транслируются в шировещательном режиме. Сотовые сети при передаче данных используют сотовые цифровые пакеты. Такие паекты работают по технологии сотовых телефонов. Данные передаются по существующим каналам для передачи речи в те моменты когда эти сети не заняты. Достоинства: быстрая переча данных. Микроволновые системы. Такая система включает в себя два радиотрансивера (приемник и передатчик) для генерации сигналов и две направленные антенны. Система работает в зоне прямой видимости либо через спутник. Микроволновая технология – самый распространенный способ передачи данных на большие расстояния. 19. Геометрическое моделирование. Представление геометрических объектов (точка, прямая, линия, плоскость, поверхность, фигура). Представление геометрических преобразований плоскости и пространства. Алгоритмы построения линий и поверхностей. Рассмотрим линейное преобразование плоскости, т. е. уравнения с помощью которых некоторые точки плоскости (x, y) ставятся в соответствии точка (x”, y”) этой же плоскости. Итак, x”=A11x+A12y+A13 ; y”= A21 y+A22y+A23. Добавим к этим уравнениям еще одно 1= A31 x+A32x+A33. это уравнение будет справедливым, если A31 =A32 =0 и A33=1. Теперь систему уравнений м/о представить в матричной форме.
Область, в которой Алгебра высказываний. Нормальные формы. Совершенные нормальные формы. Теорема существования нормальной формы. Приложение алгебры высказываний к логико-математической практике. Алгебра выск. – это раздел матем., изуч выск-я, рассм. со стороны их логич. зн-й (ист-ти или лож-ти) и логич. операций над ними. Алгебра выск. возникла в середине ХIХ века в трудах англ. матем. Буля. Высказывание – повествовательное предложение, кот. либо ист., либо ложно. Существует 5 видов логических операций. Отрицание выск. А – выск. Конъюнкция (дизъюнкция) выск. А и В – новое выск. А Импликация – выск. А Эквиваленция – выск. А 1. Всякая пропозициональная перем. есть ф-ла. 2. Если А и В – ф-лы, то 3. Других ф-л нет. классификация формул алгеб.выс-й:1. Ф-ла F(x1 …xn) наз-ся выполнимой (опровержимой) если существует ее истинная (ложная) конкретизация. 2. Ф-ла F(x1 …xn) наз-ся тавтологией или тождественно истинной (ложной) тавтологией, если любая ее конкретизация истина (ложна). Две формулы F(x1 …xn) и G(x1 …xn) будем наз-ть равносильными, если для любых конкретных высказываний А1 …Аn их конкретизации совпадают, т.е. Т1. Две формулы F и H равносильны ó формула F Конъюнктивный (дизъюнктивный) одночлен наз-ся совершенным, если в нем каждая переменная встречается только один раз, с отрицанием или без. ДНФ наз-ся с овершенной, если все конъюнктивные одночлены совершенны. КНФ наз-ся совершенной, если все дизъюнктивные одночлены совершенны. Т1. Для любой нетождественно ист. ф-лы алгебры выск. сущ-ет единств. равносильная СКНФ. Т2. Для любой нетождественно лож. ф-лы алгебры выск. сущ-ет единств. равносильная СДНФ. Приложение. А 1. От прот. А 2. Метод приведения к абсурду. А 3. Правило силлогизма. Надо найти такое С, чтобы (А
СОДЕРЖАНИЕ 1. Информация. Виды и свойства информации. Информационные процессы и технологии. Общие принципы кодирования информации и формы ее представления в ЭВМ. 2 2. Моделирование стохастических систем. Моделирование случайных величин с равномерным распределением. Методы проверки случайности данных. Моделирование случайных величин с заданным распределением. 4 3.Методы приближенного решения дифференциальных уравнений. Погрешность методов. 6 4. ЯП пролог и логическое программирование. Структура программ. Особенности исполнения. 7 5. Основы понятия "алгоритм". Алгоритм: содержательный и формализованный подходы к понятию "алгоритм". Свойства алгоритма и способы его описания. 8 6. Граф. Вершины и ребра графа. Виды графов. Пути. Связность, мосты и точки сочленения. Компоненты связности. Двудольный граф. Способы задания графа. 9 7. ЭВМ как средство обработки информации. Классификация ЭВМ. Перспективы развития вычислительной техники. 10 8. Основы анализа алгоритмов. Асимптотическая временная сложность алгоритмов. Классификация скоростей роста сложности алгоритма. О-символика. 11 9. Машина Тьюринга. Операции над машинами Тьюринга. Вычислимость по Тьюрингу частично-рекурсивных функций. Совпадение класса всех нормально вычислимых функций с классом функций вычислимых по Тьюрингу. 12 10. Элементы теории игр. Понятие об игровых моделях. Нижняя и верхняя цены игры. Принцип минимакса. Вполне определенные игры, не содержащие седловой точки. Решение игр в смешанных стратегиях. Геометрическая интерпретация игры 2x2. 13 11. Нейр. сети. Одн. перцептр. Актив. ф-ия. Лог. операц. на основе прст. перцептр. 15 12. Приближенное решение уравнений. Методы бисекции, хорд, касательных, комбинированный, итераций. Погрешность методов. 15 13. Виды компьютерной памяти. Устройства памяти, принципы их рабты и характеристики. 17 14. Классификация ППО. Программы создания рисунков. Методы представления графических изображений. Растровая и векторная графика. Системы цветов в компьютерной графике. Форматы графических файлов. 18 15. Принципы функционирования локальных вычислительных сетей. Устройства поддержки работы ЛВС. Типы ЛВС. Одноранговые сети. Сети на основе сервера. Комбинированные сети. 19 16. Моделирование стохастических систем. Общая схема метода Монте-Карло. Особенности моделирования систем массового обслуживания. Математическая модель систем массового обслуживания. 21 17. Элементы теории двойственности. Прямая и двойственная задачи линейного программирования. Основные теоремы двойственности. Применение двойственного симплексного метода. 22 18. Основные типы кабельных сред передачи данных. Узкополосная и широкополосная передача сигналов. Асинхронная передача и автоподстройка. Сетевой адаптер. Беспроводные сети. Передача "точка-точка". Инфракрасные лазерные ЛВС. Беспроводные ЛВС с радиопередачей. 23 19. Геометрическое моделирование. Представление геометрических объектов (точка, прямая, линия, плоскость, поверхность, фигура). Представление геометрических преобразований плоскости и пространства. Алг
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.019 с.) |

 игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:
игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:  .
. . В случае, если верхняя и нижняя цены совпадают
. В случае, если верхняя и нижняя цены совпадают  , то игра имеет решение в чистых стратегиях, то есть можно точно определить стратегии
, то игра имеет решение в чистых стратегиях, то есть можно точно определить стратегии  , которые выгодны для обоих сторон. Если одна сторона отойдет от своей оптимальной стратегии, то ее выигрыш от этого только уменьшится.
, которые выгодны для обоих сторон. Если одна сторона отойдет от своей оптимальной стратегии, то ее выигрыш от этого только уменьшится. в матрице такой игры является одновременно минимальным в строке
в матрице такой игры является одновременно минимальным в строке  , максимальным в столбце
, максимальным в столбце  и называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность – это решение игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно. Точка называется седловой из-за формы графика функции выигрыша в точке
и называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность – это решение игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно. Точка называется седловой из-за формы графика функции выигрыша в точке  Смешанные стратегии игрока А записываются в виде матрицы
Смешанные стратегии игрока А записываются в виде матрицы 
 , или, SB = (q1, q2,..., qi,..., qn), где сумма вероятностей появления стратегий равна 1:
, или, SB = (q1, q2,..., qi,..., qn), где сумма вероятностей появления стратегий равна 1: 












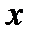
 найдем:
найдем:


 т.е.с-кор-нь
т.е.с-кор-нь



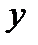




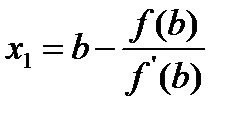 анал-но
анал-но  …
…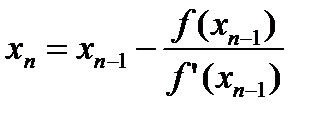
 то переходя к пределу, получим:
то переходя к пределу, получим: т.е. с – корень
т.е. с – корень
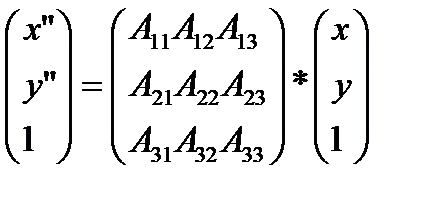 Эта матрица квадратная. Кривая на плоскости задает зависимость м/у значениями x и y координат. Эта зависимость называется функциональной. М/о задавать значения точек с помощью пар. Прямую м/о задать уравнением Ay=Bx+C. С др. стороны это же уравнение м/о задать формулой двух неизвестных
Эта матрица квадратная. Кривая на плоскости задает зависимость м/у значениями x и y координат. Эта зависимость называется функциональной. М/о задавать значения точек с помощью пар. Прямую м/о задать уравнением Ay=Bx+C. С др. стороны это же уравнение м/о задать формулой двух неизвестных  . Называется функциональной формулой прямой. Точка принадлежит прямой тогда и только тогда, когда
. Называется функциональной формулой прямой. Точка принадлежит прямой тогда и только тогда, когда  =0. Т. о. вся плоскость оказывается разделенной на три области:
=0. Т. о. вся плоскость оказывается разделенной на три области: А, кот ист. ттт, когда А – ложно.
А, кот ист. ттт, когда А – ложно. В (А
В (А  В), ист. ттт, когда А и В – ист (ложны).
В), ист. ттт, когда А и В – ист (ложны). В, ложное ттт, когда А – ист., В – ложно.
В, ложное ттт, когда А – ист., В – ложно. В, ист. ттт, когда оба приним. одинак. зн-я. Переменные вместо которых можно подставить высказывания называют позициональными или переменными высказываниями.
В, ист. ттт, когда оба приним. одинак. зн-я. Переменные вместо которых можно подставить высказывания называют позициональными или переменными высказываниями. А, А
А, А  В, А
В, А  В, А
В, А  В, А
В, А  В – ф-лы.
В – ф-лы. .
. H является тавтологией. Одной из равносильных формул является нормальная форма. Конъюнктивным одночленом от перем. x1 …xn наз-ся конъюнкция этих перем. и их отрицаний. Дизъюнктивным одн-ном от перем. x1 …xn наз-ся дизъ. этих перем. и их отрицаний. ДНФ от перем. x1 …xn наз-ся дизъ. конъюнктивных одн-в от этих перем. КНФ от перем. x1 …xn наз-ся конъ. дизъюнктивных одн-в от этих перем. Очевидно, что у данной формулы F существует неограниченно много как дизъюнктивных, так и конъюнктивных нормальных форм. Одни из них более громоздкие и сложные, другие – более простые. Среди множества дизъюнктивных (конъюнктивных) нормальных форм, которыми обладает данная формула, существует уникальная форма – единственная для данной формулы.
H является тавтологией. Одной из равносильных формул является нормальная форма. Конъюнктивным одночленом от перем. x1 …xn наз-ся конъюнкция этих перем. и их отрицаний. Дизъюнктивным одн-ном от перем. x1 …xn наз-ся дизъ. этих перем. и их отрицаний. ДНФ от перем. x1 …xn наз-ся дизъ. конъюнктивных одн-в от этих перем. КНФ от перем. x1 …xn наз-ся конъ. дизъюнктивных одн-в от этих перем. Очевидно, что у данной формулы F существует неограниченно много как дизъюнктивных, так и конъюнктивных нормальных форм. Одни из них более громоздкие и сложные, другие – более простые. Среди множества дизъюнктивных (конъюнктивных) нормальных форм, которыми обладает данная формула, существует уникальная форма – единственная для данной формулы. В – прямая т-ма. В"А – обратная.
В – прямая т-ма. В"А – обратная.  А
А 
 В – противопол.
В – противопол.  В
В 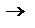
 А – противопол. к обратной. Способы док-ва т-м:
А – противопол. к обратной. Способы док-ва т-м: В"
В"  А.
А.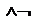 В
В  (С
(С  С).
С). С)
С)  (С
(С  В) – выполн.
В) – выполн.


