
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перенос, растяжение, поворот вокруг точки плоскостейСодержание книги
Поиск на нашем сайте
Перенос Точка (x, y) переносится в точку(x”, y”) путем перемещения на вектор (tx, ty), т. е. x” =1 *x+ 0 *y+tx; y ”=0 *x +1 *y+ty. Этому преобразованию соответствует матрица Растяжение. При таком преобразовании координата x уменьшается на cx, а y*cy. x”=cx*x +0 *y +0; y”= 0* x+cy*y +0 Матрица имеет вид: Вращение относительно начало координат. Будем поворачивать на угол Матрица: Представление точек, прямых, плоскостей в пространстве. Стандартные задачи. Над трехмерными векторами можно производить две операции: умножать на число - К * (X,Y,Z) = (K*X,K*Y,K*Z); складывать - сумма векторов Р1=(X1,Y1,Z1) и Р2=(X2,Y2,Z2) есть вектор (X1+Х2, Y1+Y2, Z1+Z2), то есть при сложении векторов соответствующие координаты складываются. Определение прямой. Теперь мы определили прямую, проходящую через две точки (X1,Y1,Z1), (X2,Y2,Z2), что можно сделать, задав уравнение этой прямой: (X-X1)*(Y2-Y1)=(Y-Y1)*(X2-X1), (Y-Y1)*(Z2-Z1)=(Z-Z1)*(Y2-Y1), (Z-Z1)*(X2-X1)=(X-X1)*(Z2-Z1). Хотя здесь приведены три уравнения, их решение определяет прямую, а не единственную точку, что связано с тем, что эти уравнения линейно зависимы так, что, задавая одну из координат, можно однозначно получить значение двух других. Так же, как и в случае двух измерений, это не единственный способ задавать прямую. Существует еще параметрический способ задания прямой, проходящей через точки Р1 иР2: P(M) = (1-M)*P1 + M*P2, или I P(M)=((1-M)*X1+M*X2, (1-M)*Y1+M*Y2, (1-M)*Z1+M*Z2), где M - действительный параметр. Параметрический вид прямой в точности совпадает с двумерным случаем. Если M = 1 дает точку Р2, а М = 0 - точку Р1. Мы можем записать параметрическое уравнение кривой в таком виде: P(M) = Р1 + M*(P2 - P1). вектор Р1 называется базовым вектором, а вектор (Р2-Р1) - направляющим вектором. Определим норму вектора (которую так же называют модулем вектора, его длиной), обозначаемую ABS(P), как расстояние от точки, определяемой вектором, до начала координат: ABS(D) = SQRT(X^2 + Y^2 + Z^2). Если вектор D=(X,Y,Z) составляет с осью X, Y, Z углы ТЕТx, TETy и TETz, то X:Y:Z = COS(TETX): COS(TETY): COS(TETZ) -/ Координаты единичного вектора назыв. направляющими косинусами. Определение плоскости. Точки плоскости задаются уравнением: N*X=K, где К - скаляр, а N - вектор, перпендикулярный плоскости Если А принадлежит плоскости, то N*A = К, заменяя К в предыдущем уравнении получим: N*X=N*A, N*(X-A)=0. откуда N*(X-A)=0 откуда (X-A) принадлежит пл-ти откуда N-норм-ый вектор к плоскости. Функциональное представление поверхности. Мы видели, что в двумерном случае кривые можно задавать с помощью функциональных зависимостей. Этот метод можно использовать для исследования поверхностей в трехмерном пространстве. Простейшей формой поверхности является плоскость с нормалью N = (N1, N2, N3), которая, как мы знаем, задается уравнением: N*X-K = N1*X+N2*Y+N3*Z-K = 0, которое можно переписать в функциональной форме: F(X)=F(X,Y,Z)=N1*X+N1*Y+N*Z-K=N*X-K, где X=(X,Y,Z). Это простое выражение позволяет нам разбить пространство на три множества: множество точек Х таких, что F(X) < 0 - отрицательная область, множество точек X, лежащих на плоскости, таких, что F(X) = 0, и множество точек Х таких, что F(X)>0 - положительная область. Если поверхность разбивает пространство на две связные области (область называется связной, если любые две точки области можно соединить кривой, целиком лежащей в этой области), то эти области можно отождествлять с областью положительных и отрицательных значений. Следует иметь в виду, что многие поверхности делят пространство на большое число компонентов. Примером такой поверхности является поверхность, задаваемая уравнением: F(X,Y,Z) = COS(Y) - SIN(Х^2+Z^2). Однако имеется ряд поверхностей, удовлетворяющих требуемому условию. Примером такой поверхности является сфера: F(X)=R^2-ABS(X)^2. Или по компонентам: F(X,Y,Z)=R^2-X^2-Y^2-Z^2. Если F(X) = 0, то Х лежит на сфере, если F(X)<0, то точка лежит вне сферы, если F(X)>0, то точка лежит внутри сферы. Функциональное представление поверхностей весьма полезно при нахождении точек пересечения поверхностей. Однако это представление особенно ценно при выяснении того, лежат ли две точки Р и Q по одну сторону от поверхности. Для этого достаточно сравнить знаки F(P) и F(Q): если они одного знака, то точки Р и Q лежат по одну сторону от поверхности, а если разного - то по разные, что означает, что любая кривая, соединяющая Р и Q, пересекает поверхность хотя бы в одной точке. Ниже приведен пример, иллюстрирующий вышесказанное.
Алгебра высказываний. Нормальные формы. Совершенные нормальные формы. Теорема существования нормальной формы. Приложение алгебры высказываний к логико-математической практике. Алгебра выск. – это раздел матем., изуч выск-я, рассм. со стороны их логич. зн-й (ист-ти или лож-ти) и логич. операций над ними. Алгебра выск. возникла в середине ХIХ века в трудах англ. матем. Буля. Высказывание – повествовательное предложение, кот. либо ист., либо ложно. Существует 5 видов логических операций. Отрицание выск. А – выск. Конъюнкция (дизъюнкция) выск. А и В – новое выск. А Импликация – выск. А Эквиваленция – выск. А 1. Всякая пропозициональная перем. есть ф-ла. 2. Если А и В – ф-лы, то 3. Других ф-л нет. классификация формул алгеб.выс-й:1. Ф-ла F(x1 …xn) наз-ся выполнимой (опровержимой) если существует ее истинная (ложная) конкретизация. 2. Ф-ла F(x1 …xn) наз-ся тавтологией или тождественно истинной (ложной) тавтологией, если любая ее конкретизация истина (ложна). Две формулы F(x1 …xn) и G(x1 …xn) будем наз-ть равносильными, если для любых конкретных высказываний А1 …Аn их конкретизации совпадают, т.е. Т1. Две формулы F и H равносильны ó формула F Конъюнктивный (дизъюнктивный) одночлен наз-ся совершенным, если в нем каждая переменная встречается только один раз, с отрицанием или без. ДНФ наз-ся с овершенной, если все конъюнктивные одночлены совершенны. КНФ наз-ся совершенной, если все дизъюнктивные одночлены совершенны. Т1. Для любой нетождественно ист. ф-лы алгебры выск. сущ-ет единств. равносильная СКНФ. Т2. Для любой нетождественно лож. ф-лы алгебры выск. сущ-ет единств. равносильная СДНФ. Приложение. А 1. От прот. А 2. Метод приведения к абсурду. А 3. Правило силлогизма. Надо найти такое С, чтобы (А
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.98.244 (0.006 с.) |


 обычно cx, cy положительны, но они могут быть и отрицательными. Например, если cx =-1, cy =1, то имеем симметрию относительно cy.
обычно cx, cy положительны, но они могут быть и отрицательными. Например, если cx =-1, cy =1, то имеем симметрию относительно cy. против часовой стрелки (положительное направление):
против часовой стрелки (положительное направление): 

 А, кот ист. ттт, когда А – ложно.
А, кот ист. ттт, когда А – ложно. В (А
В (А  В), ист. ттт, когда А и В – ист (ложны).
В), ист. ттт, когда А и В – ист (ложны). В, ложное ттт, когда А – ист., В – ложно.
В, ложное ттт, когда А – ист., В – ложно. В, ист. ттт, когда оба приним. одинак. зн-я. Переменные вместо которых можно подставить высказывания называют позициональными или переменными высказываниями.
В, ист. ттт, когда оба приним. одинак. зн-я. Переменные вместо которых можно подставить высказывания называют позициональными или переменными высказываниями. А, А
А, А  В, А
В, А  В, А
В, А  В, А
В, А  В – ф-лы.
В – ф-лы. .
. H является тавтологией. Одной из равносильных формул является нормальная форма. Конъюнктивным одночленом от перем. x1 …xn наз-ся конъюнкция этих перем. и их отрицаний. Дизъюнктивным одн-ном от перем. x1 …xn наз-ся дизъ. этих перем. и их отрицаний. ДНФ от перем. x1 …xn наз-ся дизъ. конъюнктивных одн-в от этих перем. КНФ от перем. x1 …xn наз-ся конъ. дизъюнктивных одн-в от этих перем. Очевидно, что у данной формулы F существует неограниченно много как дизъюнктивных, так и конъюнктивных нормальных форм. Одни из них более громоздкие и сложные, другие – более простые. Среди множества дизъюнктивных (конъюнктивных) нормальных форм, которыми обладает данная формула, существует уникальная форма – единственная для данной формулы.
H является тавтологией. Одной из равносильных формул является нормальная форма. Конъюнктивным одночленом от перем. x1 …xn наз-ся конъюнкция этих перем. и их отрицаний. Дизъюнктивным одн-ном от перем. x1 …xn наз-ся дизъ. этих перем. и их отрицаний. ДНФ от перем. x1 …xn наз-ся дизъ. конъюнктивных одн-в от этих перем. КНФ от перем. x1 …xn наз-ся конъ. дизъюнктивных одн-в от этих перем. Очевидно, что у данной формулы F существует неограниченно много как дизъюнктивных, так и конъюнктивных нормальных форм. Одни из них более громоздкие и сложные, другие – более простые. Среди множества дизъюнктивных (конъюнктивных) нормальных форм, которыми обладает данная формула, существует уникальная форма – единственная для данной формулы. В – прямая т-ма. В"А – обратная.
В – прямая т-ма. В"А – обратная.  А
А 
 В – противопол.
В – противопол.  В
В 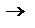
 А – противопол. к обратной. Способы док-ва т-м:
А – противопол. к обратной. Способы док-ва т-м: В"
В"  А.
А.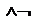 В
В  (С
(С  С).
С). С)
С)  (С
(С  В) – выполн.
В) – выполн.


