
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нейр. Сети. Одн. Перцептр. Актив. Ф-ия. Лог. Операц. На основе прст. Перцептр.Содержание книги
Поиск на нашем сайте
Нейронные сети представляют собой упрощенную модель человеческого мозга. Мозг состоит из нейронов, которые яв-ся индивидуальными процессорами. Нейроны соединяются друг с другом с помощью нервных окончаний двух типов: синапсов, через которые в ядро поступают сигналы, и аксонов, через которые нейрон передает сигнал далее. Человеческий мозг состоит примерно из 1011 нейронов. Каждый нейрон связан примерно с 1000 других нейронов (это не относится к коре головного мозга, где плотность нейронных связей намного выше). Однослойный перцептрон представляет собой концептуальную модель, которая состоит из одного процессора. Каждое соединение от входа к ядру включает коэффициент, который показывает фактор веса и обозначается с помощью веса Wi который определяет влияние ячейки Ui на другую ячейку. Положительные веса показывают усиление, а отрицательные запрещение. Совместно с входами в ячейку они определяют поведение сети. Схема однослойного перцептрона представлена на рис. Ячейка включает три входа (u1, u2 и u3). Кроме этого, есть вход смещения (W0), о котором будет рассказано позже. Каждое входное соединение имеет вес (w1, w2 и w3 ). Наконец, существует единый выход, О. Состояние нейрона обозначено как Y и определяется уравнением. Выражение, показанное в уравнении, яв-ся функцией, которая суммирует сигналы на всех входах с учетом веса, а затем добавляет смещение. Затем результат передается в активационную функцию, которая может быть определена так, как показано в уравнении (в данном случае функция яв-ся пороговой). y = -1, если (y<=0) (5.2) y = 1, если (y> 0) Если значение состояния больше нуля, то выходное значение будет равно 1. Иначе оно составит -1. Хотя однослойный перцептрон яв-ся очень простой моделью, ее возможности весьма велики. Например, можно легко сконструировать базовые логические функции.
функция И имеет значение 1, если оба входа равны 1, в противном случае функция возвращает значение 0. Поэтому если заданы оба входа (вектор u = (1,1)), то, используя активационную функцию в качестве порога, получим следующий результат: Y = смещение + u1*w1, + u2*w2 или 1 = nopoг(-1+(1*l)+(l*1)). Теперь попробуем подставить вектор и = (0,1): Y = смещение + u1*w1, + u2*w2 или 1 = порог(-1 + (0*1)+(1*1)).
Как показывают оба примера, модель простого перцептрона правильно реализует логическую функцию И (а также функции ИЛИ и НЕ). Приближенное решение уравнений. Методы бисекции, хорд, касательных, комбинированный, итераций. Погрешность методов. Приближённое решение дифференциальных уравнений, получение аналитических выражений (формул) или численных значений, приближающих с той или иной степенью точности искомое частное решение дифференциального уравнения. Метод бисекций. Пусть дано ур-ие f(x)=0 где f(x)-непрерывно на некотором конеч или бесконеч интерв. Конем этого ур. Назовем " число обращ-е f(x) в 0, если f(x0)=f /(x0)=…fk-1(x0)=0, то x0 корень кратности к точно решить данное ур-ие не всегда удается, будем гов-ть, что x—есть приближенное решение ур-ия с точн-ю e если |a-x––| <=e,где а точный корень –e<= a-x––<=e или a-e<=x––<=a+e.Задача о нахожд приближ корня обычно реш-ся в 2 этапа 1) отдел-ся корень т.е. ищется по возм-ти небольш отр-ок [a, b] содерж ровно один корень. 2) корень уточн-ся до нужной точности. 1) а) отделение корня м.о. пр-ти графически. б) если график сложен, то ур-е мо переписать в виде g(x) =f(x) (и построить гр-ки y=g(x), y=f(x) и точка пересеч б.т. корень). в) мо для отделен корня исп-ть. теор. Т.если непрерыв ф-я на концах отр приним-ет значен разных знаков, то на отр-ке она имеет по кр-не. мере один корень. Если ф-я монотонна, то кор-нь один. Пусть изв-но, что корни Ур-я нах-ся на конц отр-ка [a,b]разделим отрезок на равные части точками a=a0<a1<…<an=b и проверим знаки на концах отр-ка [ai,ai+1] i=0,n-1 если условие теор вып-ся отр-к содерж корень, алгор-м метода м.б. следующим а,в концы отрезка, n-кол-во отр-ов деления.
2) одним из простейших способов уточнения корня явл-ся метод бисекции сост-ий в следующем: пусть на отр. [a,b] yf[-cz ровно 1 корень уровн. Найдем корень с точн-ю e. Разделим отр. Пополам. Точкой x1 =(a+b)/2, половину содерж корень вновь делим пополам итд. Процесс прекращ, когда длина отр-ка не станет <=2e тогда за приближ значение корня x–– возьмем середину этого отр-ка. Алгоритм следующий.
Теорема явл-ся достаточной но не обязат для сходимости. Геометрич смысл метода итераций.
Алгоритм имеет вид Методами хорд и касс-ых. М-д хорд.
Пусть корень Ур-ния f(x)=0, [a,b] допустим, что на [a,b] существ. f’’(x), к-ое не мен. знак. Пусть для определ-ти f(a)<0. Пусть f’’>0 (рис.): провед. хорду АВ и найдем ее пересеч. с осью x. Пусть А1 пересечение y=f(x) и прямой x=x1, проводим хорду А1В, пусть x2 – ее пересеч. с осью x и т.д. Получ. ∞ числов. послед-ть {xn}. Для нахожд. xi используем Ур-ние прямой, прох. ч/з 2 точки:
В послед-сти xn: a=x0<x1<…<xn<…<b т.е. посл-ть xn имеет предел, как возрост-ая и ограниченная сверху, т.е. перейдя к пределу:
М-д касательных. Пусть корень ур-ния f(x)=0 отделен на отрез. [a,b], причем f’’ не меняет знака на [a,b]. Возьмем для опред-сти f(a)<a, f’’>0
Провед. касат. к тому концу дуги АВ в к-ром f*f’’>0. Пусть x1 ее пересеч. с Ox обозначим ч/з b1 пересеч. прямой x=x1 и дуги АВ. Провед. касат. в т.В1 пусть x2 ее пересеч. с Ox и т.д. Получ. ∞ послед-ть {xn} имеющую предел как убывающая и огранич. xn – б/м искать из ур-ния касат. Ищем x1: y-f(b)=f’(b)(x-b), полагая y=0 x=x1
т.к.
На практике для получ. корня с точн. ε заканчив. вычисл., когда Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.252.187 (0.011 с.) |

 Y = w0 + u1*w1 + u2*w2 + u3*w3
Y = w0 + u1*w1 + u2*w2 + u3*w3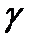





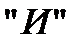

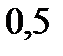












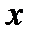
 найдем:
найдем:


 т.е.с-кор-нь
т.е.с-кор-нь



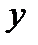




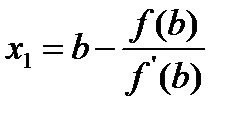 анал-но
анал-но  …
…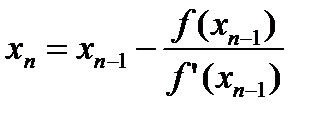
 то переходя к пределу, получим:
то переходя к пределу, получим: т.е. с – корень
т.е. с – корень



