
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Видиме випромінювання (видиме світло)Содержание книги Поиск на нашем сайте
МОДУЛЬ 5. «ОПТИКА» ОСНОВИ ТЕОРІЇ Далі розглянемо особливості електромагнітних хвиль, які сприймає око людини, тобто видиме випромінювання, або ж видиме світло. Розділ фізики, в якому вивчаються світлові явища, називається оптикою.
Геометрична оптика Видиме випромінювання (видиме світло) Розвиток уявлень про світло. Історично перша теорія світла була корпускулярною. Ще Піфагор (приблизно VІ сторіччя до н.е.) вважав, що світло – це потік дуже малих частинок (корпускул), що їх випромінюють тіла; при потраплянні в око людини ці частинки викликають відчуття кольору. Корпускулярна теорія, розвинута і вдосконалена Ньютоном, панувала до початку 19-го сторіччя. Паралельно корпускулярній розвивалась хвильова теорія. Вона розглядала світло як хвильовий процес. На початку 19–го сторіччя відкриття явищ інтерференції та дифракції, які можна було пояснити тільки хвильовими властивостями світла, вирішило питання на користь хвильової теорії. Корпускулярну ж теорію було відкинуто наукою як таку, що суперечить експериментальним фактам.Пізніше були встановлені експериментальні дані, які теорія Максвела пояснити не може. Недостатність хвильових уявлень про світло вперше було виявлено при спробі пояснити загадковий характер теплового випромінювання розжарених тіл. Тоді було введено поняття про кванти електромагнітного випромінювання, з цього почалась квантова фізика. На сучасному рівні розвитку фізики говорять про корпускулярно–хвильовий дуалізм, світло – це одночасно і хвиля, і потік частинок (фотонів). Виявилось, що не тільки хвиля має переривичасту (дискретну) природу, тобто складається з найменших порцій енергії (квантів), але й мікрочастинки (електрони, протони, нейтрони) одночасно є і корпускулами, і хвильовим процесом (так звані хвилі де – Бройля) Але спочатку розглянемо явища, в яких світло розглядається як електромагнітна хвиля. Природу світлових хвиль було встановлено Максвелом: у 1865 році він дійшов до висновку, що світло – це електромагнітне явище. Шкала довжин хвиль для різних типів електромагнітного випромінювання показана на рис. 5.1.1. Шкалу наведено в логарифмічному масштабі, нанесені на ній цифри є показниками степеня числа 10; за одиницю прийнято довжину хвилі Електромагнітна теорія світла Максвела дозволила пояснити велику кількість оптичних явищ і тому отримала загальне визнання.
Видиме світло (світлове випромінювання). Світлове випромінювання (видиме світло) є електромагнітними хвилями з діапазоном довжин хвиль у вакуумі від λ ф (фіолетове) ≈ 390 нм до λ ч(червоне) ≈ 760 нм. Як правило, заокруглюючи, вважають цей діапазон рівним у нанометрах (400 – 800) нм; у мікрометрах (0,4 – 0,8) мкм або (0,4 – 0,8)∙10 -6 м. Нагадаємо, що 1 мкм називають ще 1 мікроном. Враховуючи зв’язок між довжиною хвилі, швидкістю розповсюдження с і частотою коливань ν, можна записати:
де с = 3·10 8 м/с – швидкість світла у вакуумі. Довжинам хвиль видимого світла відповідає частотний інтервал від 7,5·1014 Гц (фіолетове) до 4·1014 Гц (червоне). Швидкість світла в середовищі:
де с – швидкість світла у вакуумі; n – абсолютний показник заломлення середовища. Абсолютним показником заломлення світла називається величина, яка показує в скільки разів швидкість світла у вакуумі більша, ніж у даному середовищі:
Закони геометричної оптики В ізотропному середовищі світло поширюється прямолінійно. Лінія, вздовж якої переміщується фронт хвилі, називається променем. Напрямок поширення світла змінюється на межі поділу середовищ з різними оптичними густинами (рис. 5.1.2.). Розглянемо закони, яким підлягають оптичні явища, що відбуваються на межі поділу двох прозорих середовищ. Ці оптичні явища описуються законами геометричної оптики. 1. Закон відбивання світла: а) промінь падаючий, промінь відбитий і перпендикуляр, поставлений у точці падіння променя лежать в одній площині; б) кут відбивання променя дорівнює куту його падіння. 2. Закон заломлення світла: а) промінь падаючий і промінь заломлений лежать в одній площині з перпендикуляром, поставленим у точці падіння променя до поверхні поділу двох середовищ; б) відношення синуса кута падіння до синуса кута заломлення для даних середовищ є величина стала і називається показником заломлення другого середовища відносно першого (відносний показник заломлення n21):
де
n 1 і n 2 – абсолютні показники заломлення.
Оптична густина середовища характеризує залежність швидкості світла від природи середовища і вимірюється абсолютним показником заломлення. Оптична густина вакууму дорівнює одиниці за визначенням, а для повітря з великим ступенем точності можна теж вважати n=1.
5.1.1.3. Явище повного внутрішнього відбивання Це явище спостерігається при відбиванні світлових хвиль, що йдуть із середовища з більшою оптичною густиною на межу із середовищем менш оптично густим, повністю повертаються в перше середовище. Повне внутрішнє відбивання має місце при переході світлового променя з оптично більш густого середовища Якщо промінь 1О1' піде в зворотному напрямку (із оптично менш густого середовища
Явище повного внутрішнього відбивання має широке застосування в оптиці. На ньому базується дія приладів для визначення коефіцієнта заломлення речовин рефрактометрів. Використання світловодів призвело до появи цілого напрямку – волоконної оптики. Найпростіший світловод – це пучок з величезної кількості прозорих гнучких ниточок, витягнутих спеціальним чином з розплаву скла. Такі світловоди використовують для передачі світла та зображення в оптоелектроніці, медицині (широко відоме використання так званого зондування шлунка та інших органів). Цікаво, що оброблення (огранювання) алмаза (тобто отримання діаманта) проводиться так, щоб для якомога більшої кількості променів світла, що падають на нього, відбувалось повне відбивання світла. Повне відбивання світла від оптично менш густих шарів нагрітого повітря, що знаходяться поблизу розігрітої поверхні Землі в пустині, є причиною появи так званих міражів. Закони відбивання та заломлення світла пояснюють хід променів у плоскому дзеркалі та створення дзеркального зображення в ньому; хід променів через плоско-паралельну пластинку; призму. Всі ці використання законів відбивання та заломлення світла розглянуто далі в розділі 5.3 посібника як приклади розв’язування задач з оптики. Хвильова оптика Інтерференція світла Явище інтерференції світла Інтерференцією називають явище, що виникає при накладанні двох (або більше) хвильових процесів, які мають однакові частоти і напрям коливань, і виражається у перерозподілі енергії хвиль у просторі. Це явище для механічних (пружних) хвиль вже розглянуто в 1.1.8.4, тут же більш детальніше проаналізуємо накладання світлових хвиль, що не є пружними. Якщо у просторі існують два джерела світлових хвиль, то в кожній точці, куди приходять хвилі від обох джерел, відбувається складання коливань. Відомо, що два гармонічних коливання одного напрямку й однакової частоти, x1 = A1sin(wt + j1) та x2 = A2sin(wt + j2), (5.1.4.) при складанні дають гармонічне коливання тієї ж частоти w. При цьому амплітуда А результуючого коливання x = x 1+ x 2 зв'язана з амплітудами А 1 і А 2 коливань, що складаються, співвідношенням:
Зазначимо, що x1 і x2 у формулі (5.1.4.) може позначати будь-яку фізичну величину, яка змінюється за гармонічним законом при розповсюдженні хвиль (наприклад, для пружних хвиль – механічний зсув частинок середовища). Для світлових явищ маємо справу з гармонічними змінами напруженості електричного та магнітного поля. Енергія гармонічного коливання пропорційна квадрату його амплітуди. Тому на підставі співвідношення (5.1.5.) можна записати: W = W 1 + W 2 +2 Як бачимо, енергія W результуючого коливання не дорівнює, взагалі кажучи, сумі енергій W 1 і W2 коливань, що складаються: W ¹ W 1 + W 2. З формули (5.1.6.) випливає, що в тих точках простору, де різниця фазD j = j 1 - j 2 хвиль, що туди прийшли, задовольняє умові: D j = 2 kp (k = 0, ± 1, ± 2, …), (5.1.7.) тобто cos Dj =+1, амплітуда і енергія результуючого коливання є максимальними:
і W = Wmax = В цих точках хвилі максимально підсилюють одна одну (рис. 5.1.9, а).
У тих точках, де різниця фаз хвиль задовольняє умові: D j = (2 k + 1) p, тобто cosDj = -1, амплітуда і енергія результуючого коливання є мінімальною:
W = Wmin = В цьому випадку хвилі максимально послаблюють одна одну (див.рис. 5.1.9, б). Зокрема, якщо амплітуди хвиль є однаковими, тобто W 1 = W 2, то Wmax = 4 W 1, а Wmin = 0. В цьому випадку хвилі повністю гасять одна одну. 5.1.2.1.2. Когерентність Повсякденний досвід показує, що вмикання двох джерел світла (наприклад, двох лампочок) не приводить до інтерференції - у будь-якій точці простору освітленість дорівнює сумі освітленостей, створюваних кожним окремим джерелом. Причина відсутності інтерференції в даному випадку пояснюється наявністю у світла квантових властивостей (детальніше в наступному розділі): випромінювання світла атомами відбувається не неперервно, а окремими короткими імпульсами. Хвиля, випущена в результаті одного акта випромінювання, має вид "куска" монохроматичної хвилі, названого хвильовим цугом. Миттєву картину випромінювання, яке йде від одного атома, схематично зображено на рис. 5.1.10 (вгорі); внизу дано "миттєвий профіль" вектора напруженості Середню тривалість t одного акта випромінювання називають часом когерентності; як правило t не більше 10-8 с. Довжина цугу хвиль, випромінюваного за час когерентності, як правило, не перевищує декількох десятків сантиметрів. При цьому початкова фаза електромагнітної хвилі, випромінюваної атомом, змінюється випадковим способом з кожним новим актом випромінювання, тобто з кожним новим цугом. Нехай два абсолютно однакових атоми випромінюють світло незалежно один від одного. Для спрощення будемо вважати, що випромінювані ними хвилі мають однакові частоти і напрямки вектора
У кожній точці простору, куди приходять цуги хвиль від обох атомів, у кожен момент часу має місце співвідношення (5.1.6.), де j 1 - j 2 = D j - різниця фаз цугів, що інтерферують. Через час t ці цуги пройдуть точку спостереження і на зміну їм прийдуть нові цуги, що теж інтерферують. Однак різниця фаз D j тепер буде іншою. Через неузгодженість актів випромінювання обох атомів різниця фаз швидко (через час порядку 10-8 с) і безладно змінюється. Відповідно до цього швидко і безладно змінюють одна одну окремі інтерференційні картини. Людське око має здатність усереднювати світлове сприйняття, що відбувається за час приблизно рівний 0,1 с. Тому воно не в змозі розрізнити окремі інтерференційні картини і сприймає лише усереднений ефект, тобто рівномірний розподіл освітленості. Дійсно, усереднюючи співвідношення (5.1.6.) і беручи до уваги, що < cosa > = 0, знаходимо: < W > = W 1 + W 2 +2 Отриманий результат означає звичайне додавання енергій хвиль, тобто відсутність інтерференції (порівняємо формули (5.1.8.) і (5.1.10.)). Як бачимо, навіть два зовсім ідентичні атоми внаслідок переривчастого характеру і неузгодженості їхніх випромінювань не дають інтерференції. З цієї ж причини неможливо спостерігати інтерференцію і від двох незалежних макроскопічних джерел світла. Із сказаного випливає, що для одержання стійкої інтерференційної картини необхідно, щоб у кожній точці спостереження різниця фаз коливань не змінювалася з часом. Когерентними називають хвилі однакової частоти, якщо різниця їх фаз є незмінною у часі. Інтерферувати можуть лише когерентні хвилі. Таким чином, умову когерентності, виконання якої необхідне для спостереження результату інтерференції (проявляється в наявності максимумів та мінімумів в розподілі результуючої інтенсивності) можна записати скорочено так: 1) Джерела таких хвиль називають когерентними. Джерела світла звичайного типу (не лазерні) не є когерентними. Звичайно, це не значить, що інтерференцію спостерігати не можна в принципі. Для цього потрібно створити якимось чином когерентні джерела, наприклад отримати їх від однієї хвильової поверхні, направивши їх різними шляхами в одну точку (метод поділу хвильового фронту).
Дифракція світла Дифракція на щілині Освітимо діафрагму Д з вузькою довгою щілиною (рис. 5.1.14,а) паралельним пучком монохроматичного світла, який можна одержати, помістивши точкове джерело світла С у фокусі збирної лінзи Л 1. За щілиною поставимо збирну лінзу Л 2 і в її фокальній площині помістимо екран Е. Вид зверху представлений схематично на рис. 5.1.14, б (ширина щілини а на цьому рисунку збільшена у сотні разів для ясності рисунка). Згідно з принципом Гюйгенса кожна точка щілини є джерелом вторинних сферичних хвиль (на рис. 5.1.14, в стрілками позначені напрямки променів, що виходять з довільної точки щілини; пунктирною лінією зображений фронт вторинної хвилі). Вторинні хвилі інтерферують і на екрані Е спостерігається інтерференційна картина. Розглянемо промені, які йдуть під кутом j до напрямку світла, що падає на екран. Всі вони зберуться лінзою Л 2 у деякій точці Р екрану Е. Позначимо через D різницю ходу між крайніми променями. При цьому врахуємо, що лінза Л 2 не вносить додаткової різниці ходу.
У напрямку j = 0 всі промені мають однакові фази і тому підсилюють один одного при накладанні у точці О - центрі екрана (рис. 5.1.14, б). Тут спостерігається максимум інтенсивності світла. Було показано за допомогою спеціального методу (метод зон Френеля), що умовою мінімумів буде: a sin j = kl, k = ± 1, ± 2, …. (5.1.15) а умовою максимумів: a sin j = (2k + 1) Зазначимо, що на практиці замість точкового джерела С (рис. 5.1.14, а) звичайно використовують вузьку щілину, паралельну тій, на якій відбувається дифракція. Різні точки щілини дають дифракційні картини, зміщені вздовж осі у так, що картина, яка спостерігається, "витягується" уздовж осі у і являє собою чергування темних і світлих смуг. При цьому зі збільшенням k інтенсивність світла в максимумі зменшується. Найбільша частка, більше 90 % усієї світлової енергії припадає на центральний максимум, тобто на область, обмежену першими мінімумами (див. рис. 5.1.16, N = 1). Поляризація світла Закон Брюстера Поляризоване світло можна отримати при відбиванні та заломленні на границі поділу двох середовищ, або ж при проходженні світла крізь анізотропні середовища (це, наприклад, деякі кристалічні тіла, які мають різні властивості пропускання світлових хвиль залежно від напрямку їхніх коливань).
Розглянемо поляризоване світло в процесі відбивання і заломлення. Нехай природний промінь АО падає на поверхню прозорого ізотропного діелектрика, наприклад на скляну пластину (рис. 5.1.20). Світлові коливання природного променя завжди можна розкласти у двох взаємно перпендикулярних напрямках. Очевидно, результуючі вектори складових світлових коливань у цих напрямках у природному промені будуть за величиною однаковими. Тому природний промінь, що падає на пластинку буде зображений коливаннями з рівною кількістю стрілок та крапок. Відбитий і заломлений промені на межі діелектрика стають частково поляризованими. У відбитому промені ОВ переважають коливання, позначені крапками, а в заломленому промені ОЗ - коливання, позначені стрілками. В цьому можна переконатися, взявши другу скляну пластинку або дзеркало. Якщо дзеркало-аналізатор розмістити перпендикулярно до площині малюнка, то за будь-яких кутів падіння Англійський фізик Брюстер, досліджуючи поляризацію світла під час відбивання, встановив, що для будь-якого діелектрика є певний кут падіння, при якому відбитий промінь стає повністю поляризований. Такий кут падіння називають кутом повної поляризації світла. Величину цього кута визначають за законом Брюстера (1815 р.): tgi 0 = де i0 – кут повної поляризації; Наприклад для скла, що має показник заломлення n = 1,5; i 0 ≈ 560. Запишемо закон Брюстера та закон заломлення світла:
Співставивши, знайдемо, що cos i0 = sin тому
Таким чином, при повній поляризації відбитого променя відбитий і заломлений промені взаємно перпендикулярні. Механізм поляризації світла в процесі відбивання та заломлення на межі вакуум – діелектрик в основних рисах зводиться до наступного. Досягнувши діелектрика, виділені нами складові падаючої хвилі спричинятимуть відповідні вимушені коливання електрично заряджених частинок атомів. З електромагнітної теорії відомо, що такі коливання заряджених частинок будуть джерелами випромінювання плоскополяризованих електромагнітних хвиль. Подібно для мініатюрної антени максимум випромінювання їх відбувається в напрямку, перпендикулярному до напрямку коливань. Вторинні хвилі з коливаннями світлового вектора, що перпендикулярні до площини коливань утворюють відбитий промінь; він буде переважно поляризованим (а при падінні під кутом Брюстера – повністю поляризованим). Вторинні хвилі з коливаннями світлового вектора, що паралельні площині коливань, наклавшись на падаючу хвилю, утворять заломлену хвилю. Ця хвиля буде частково поляризованою завжди, але при куті Брюстера – максимально частково поляризованою. Щоб заломлений пучок променів мав великий ступінь поляризації, природне світло спрямовують під кутом повної поляризації не на одну, а на кілька плоско - паралельних пластин, складених у стопу.
5.1.2.3.4. Поляризація розсіяного світла Явищеполяризації розсіяного світла виникає внаслідок проходження природного пучка світла крізь каламутне середовище – туман, рідину, колоїдний розчин, в якому містяться завислі часточки, що зрівнянні з довжиною ЕМХ. Пучок світла з різними напрямками коливань світлових векторів За законом Релея інтенсивність розсіяного світла пропорційна частоті коливань у четвертому ступені (або ж обернено пропорційна довжині хвилі у четвертому ступені):
або
Тут a та b – коефіцієнти пропорційності. Тому при проходженні білого світла через каламутне середовище розсіяне світло набуває блакитного відтінку. Світло на виході (те що пройшло каламутне середовище) стає червонуватим.
5.1.2.3.5. Оптична анізотропія двозаломлювальних кристалів
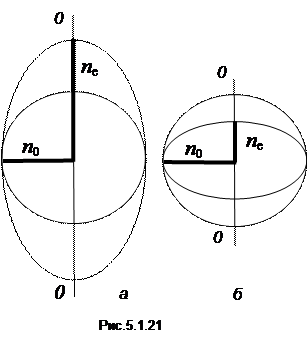
Відносна діелектрична проникність ε характеризує реакцію середовища на дію електричного поля. Отже, показник заломлення n залежить від того, як діє на середовище електричний вектор Для обох випадків характерно, що в кристалі існує фізично виділений напрямок (вздовж півосі nе). Його називають оптичною віссю кристала – всі напрямки, перпендикулярні оптичній осі, є рівноправними. Такі кристали називають одновісними. Значення n о і nе, а також орієнтація осі відносно характерних кристалографічних напрямків в кристалі визначається конкретною структурою кристалічної гратки. Наприклад, у кристалі кальциту (безбарвному мінералі, що називається також ісландським шпатом; хімічна формула СаСО3) n о = 1,658 та nе = 1,486 (для жовтого світла, λ = 0,5893 мкм), а напрямок оптичної осі збігається з напрямком найкоротшої просторової діагоналі елементарної комірки. Залежність показника заломлення від коливань світлового вектора приводить до того, що промінь природного світла, попадаючи у кристал, розщеплюється на два промені. Це явище отримало назву подвійного променезаломлення. Його ілюструє рис. 5.1.22, де зображено кристалічну пластинку з оптичною віссю ОО , що паралельна площині рисунку. Коливання, перпендикулярні площині рисунку (їх зображено крапками), утворюють з оптичною У незвичайному промені кут між напрямком коливань світлового вектора і оптичною віссю може змінюватися від Величину nе не слід плутати з показником заломлення незвичайного променя: останній залежить від напрямку променя, в той час як nе – константа. Обидві величини збігаються, коли незвичайний промінь поширюється перпендикулярно оптичній осі кристала. 5.1.2.3.6. Призма Ніколя На явищі подвійного променезаломлення засновано більшість поляризаційних пристроїв. Типовим прикладом такого пристрою (поляризатора) є призма Ніколя (див. рис. 5.1.23).
nе < nб < nо. Розпил роблять таким, щоб кут падіння α звичайного променя на межу поділу був більшим граничного – тоді звичайний промінь зазнає повного внутрішнього відбиття і відходить убік. Незвичайний же промінь без перешкод проходить через прошарок канадського бальзаму й іншу частину призми.
5.1.2.3.7. Дихроїзм двозаломлювальних кристалів. Поляроїди У деяких кристалах, у тому числі і у турмаліні, звичайний промінь поглинанається значно сильніше ніж незвичайний. Це явище називають дихроїзмом. При достатній товщині дихроїчних кристалів (для турмаліну ця товщина становить приблизно 1 мм) один із применів повністю поглинається, а інший дає на виході із кристалу плоскополяризоване світло. Явище дихроїзму використовується при виготовлені поляроїдів – прозорих полімерних плівок, які містять велику кількість однаково орієнтованих дихроїчних кристалів, наприклад, герапатиту (сірчанокислого йодхініну). В цих кристалах звичайний промінь практично повністю поглинається на шляху приблизно 0,1 мм. Поляроїдна плівка є порівняно недорогою, еластичною, може мати велику площу, майже однаково пропускає всі довжини хвиль видимого світла (в той час як турмалін пропускає в основному промені зеленого кольору). Поляризоване світло використовується для багатьох наукових і практичних цілей. З його допомогою хіміки вивчають структуру молекул, геологи – будову мінералів, інженери – деформацію матеріалів, біологи – властивості субклітинних утворень, фізики – характер міжмолекулярних взаємодій, зокрема, процеси переносу енергії; астрономи – атмосфери планет і міжзоряний простір, метеорологи – динаміку атмосфери. Різноманітними є і чисто практичні застосування поляризованого світла у світлотехніці, оптичній обробці інформації, електричних вимірюваннях, аналітичній хімії, цукровому виробництві і багатьох інших галузях. Дисперсія світла. Спектри. Явище дисперсії світла Дисперсією називають явище залежності абсолютного показника заломлення світла даного середовища від довжини хвилі, тобто залежність n (λ). Оскільки довжина хвилі зв`язана з частотою світла:
а швидкість розповсюдження світла в середовищі обернено пропорційна абсолютному показнику заломлення:
то можна сказати, що дисперсія – це явище залежності показника заломлення світла (або швидкості розповсюдження світла в середовищі) від довжини (або частоти) хвилі. Ці залежності можна записати так: n ( Часто дисперсією називають величину похідної абсолютного показника заломлення світла даного середовища по довжині хвилі:
Якщо показник заломлення зменшується при збільшенні довжини хвилі видимого світла, то дисперсія називається нормальною ( При нормальній дисперсії швидкість червоного світла, яке заломлюється найменше, буде найбільшою, а швидкість фіолетового – найменшою. Якщо ж показник заломлення збільшується при збільшенні довжини хвилі видимого світла, то дисперсія називається аномальною ( Було встановлено, що нормальна дисперсія спостерігається для світла з довжинами хвиль, що далекі від довжин хвиль, на яких середовище поглинає світло, а аномальна дисперсія – в області довжин хвиль, де середовище поглинає світло (говорять, в смугах поглинання). Зрозуміло, що у вакуумі, де по визначенню показник заломлення дорівнює одиниці, швидкість світла для будь-якої довжини хвилі (тобто світла любого кольору - від фіолетового до червоного) буде одинаковою. Таким чином, у вакуумі дисперсія відсутня.
Явище дисперсії приводить до того, що при проходженні через призму білого світла (де є всі довжини хвиль) світло буде розкладатись у спектр. Тобто, промені різних довжин хвиль будуть по–різному відхилятись призмою. Оскільки кут відхилення світла призмою залежить від показника заломлення:
Спектральні прилади Розкладення світла в спектр лежить в основі роботи призмових спектральних приладів, що дозволяють аналізувати спектральний склад випромінювання та поглинання різних матеріалів. Спектроскоп – найпростіший призмовий спектральний прилад, що використовується для дослідження спектрального складу світла, тобто спостереження спектрів. Тому він обов’язково містить у собі пристрій для розкладання світла за довжинами хвиль. У призмовому спектроскопі таким пристроєм є призма П із скла з великою дисперсією. Відмітимо, що існують і інші спектральні прилади, в яких диспергуючим пристроєм
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.167 (0.02 с.) |

 = 1м. Видимому світлу на цій шкалі відповідає вузький інтервал довжин хвиль від 3,9∙10 -7 до 7,6∙10 -7 м.
= 1м. Видимому світлу на цій шкалі відповідає вузький інтервал довжин хвиль від 3,9∙10 -7 до 7,6∙10 -7 м.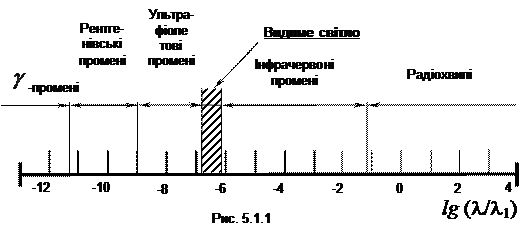
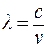 ,
,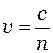 ,
,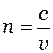 . (5.1.1)
. (5.1.1)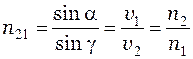 , (5.1.2.)
, (5.1.2.)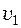 і
і 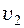 – швидкості поширення світла в першому і другому середовищі;
– швидкості поширення світла в першому і другому середовищі;
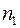 в оптично менш густе середовище
в оптично менш густе середовище 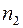 (
(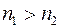 ). При граничному куті падіння
). При граничному куті падіння 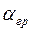 заломлений промінь 1О1' ковзає вздовж поверхні поділу цих середовищ (рис. 5.1.3).
заломлений промінь 1О1' ковзає вздовж поверхні поділу цих середовищ (рис. 5.1.3).  маємо:
маємо: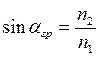 .
.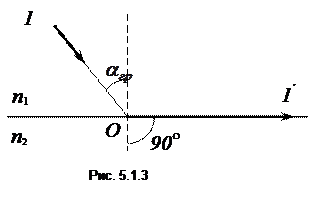 Граничні кути повного відбивання для деяких матеріалів: скло – 30○ – 43○; вода – 49○; алмаз – 24○.
Граничні кути повного відбивання для деяких матеріалів: скло – 30○ – 43○; вода – 49○; алмаз – 24○. . (5.1.5)
. (5.1.5) cos(j 1 - j 2). (5.1.6.)
cos(j 1 - j 2). (5.1.6.) ;
; . (5.1.8.)
. (5.1.8.)
 ;
; 
 . (5.1.9)
. (5.1.9)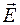 електричного поля уздовж деякого напрямку х.
електричного поля уздовж деякого напрямку х. 
 =
=  ; 2)
; 2) 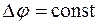 . (5.1.11)
. (5.1.11)
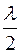 , k = ± 1, ± 2, …. (5.1.16)
, k = ± 1, ± 2, …. (5.1.16)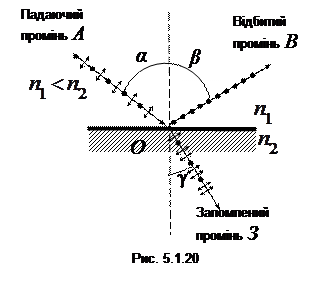 промінь ОВ відбиватиметься від нього, помітно не змінюючи інтенсивність. Навпаки, коли дзеркало розміщувати під будь-якими іншими кутами до поверхні пластинки, то можна помітити різке зменшення інтенсивності відбитого променя. Аналогічно поводиться і заломлений промінь ОЗ.
промінь ОВ відбиватиметься від нього, помітно не змінюючи інтенсивність. Навпаки, коли дзеркало розміщувати під будь-якими іншими кутами до поверхні пластинки, то можна помітити різке зменшення інтенсивності відбитого променя. Аналогічно поводиться і заломлений промінь ОЗ.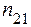 , (5.1.19)
, (5.1.19)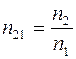 – відносний показник заломлення другого середовища відносно першого.
– відносний показник заломлення другого середовища відносно першого.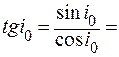
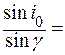
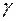 ,
,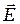 спричинює в частинках відповідні коливання електронів. Ці коливання стають джерелами випромінювання вторинних світлових хвиль. Коливання світлового вектора у вторинній хвилі відбувається в площині, що перетинає напрямок коливання зарядженої частинки. Тому розсіяне світло в напрямку, перпендикулярному до променя, що проходить, буде повністю поляризованим. У цьому можна переконатися, спостерігаючи за допомогою поляроїда збоку за пучком світла, що проходить у кюветі з водою.
спричинює в частинках відповідні коливання електронів. Ці коливання стають джерелами випромінювання вторинних світлових хвиль. Коливання світлового вектора у вторинній хвилі відбувається в площині, що перетинає напрямок коливання зарядженої частинки. Тому розсіяне світло в напрямку, перпендикулярному до променя, що проходить, буде повністю поляризованим. У цьому можна переконатися, спостерігаючи за допомогою поляроїда збоку за пучком світла, що проходить у кюветі з водою.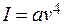 ,
,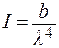 .
. Анізотропними називають середовища, фізичні властивості якого в різних напрямках є різними. Практично всім кристалам притаманна анізотропія оптичних властивостей. Виняток складають кристали найвищої, кубічної симетрії (такими, наприклад, є кристали хлористого натрію, тобто всім відомої кухонної солі). Оптичні властивості речовин характеризуються, зокрема, показником заломлення n, який виражається через відносну діелектричну проникність ε:
Анізотропними називають середовища, фізичні властивості якого в різних напрямках є різними. Практично всім кристалам притаманна анізотропія оптичних властивостей. Виняток складають кристали найвищої, кубічної симетрії (такими, наприклад, є кристали хлористого натрію, тобто всім відомої кухонної солі). Оптичні властивості речовин характеризуються, зокрема, показником заломлення n, який виражається через відносну діелектричну проникність ε: 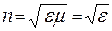 (тут вважаємо відносну магнітну проникність рівною одиниці, μ =1, бо більшість оптично анізотропних речовин практично не підсилюють і не ослабляють зовнішнє магнітне поле).
(тут вважаємо відносну магнітну проникність рівною одиниці, μ =1, бо більшість оптично анізотропних речовин практично не підсилюють і не ослабляють зовнішнє магнітне поле).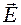 електромагнітного поля. Фізичні величини ε і n в ізотропному середовищі мають однакові значення для всіх напрямків електричного вектора (вони є скалярними), у випадку ж анізотропного середовища значення ε і n залежать від напрямку вектора
електромагнітного поля. Фізичні величини ε і n в ізотропному середовищі мають однакові значення для всіх напрямків електричного вектора (вони є скалярними), у випадку ж анізотропного середовища значення ε і n залежать від напрямку вектора 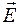 (такі величини називаються тензорами). Залежність показника заломлення від напрямку
(такі величини називаються тензорами). Залежність показника заломлення від напрямку 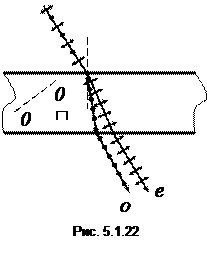 віссю кут
віссю кут 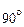 ; їм відповідає показник заломлення n о. Коливання, що відбуваються у площині рисунку (зображені стрілками), утворюють з оптичною віссю кут, відмінний від
; їм відповідає показник заломлення n о. Коливання, що відбуваються у площині рисунку (зображені стрілками), утворюють з оптичною віссю кут, відмінний від 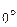 до
до 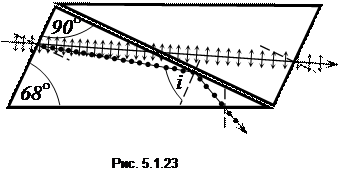 Таку призму виготовляють із ісландського шпату, розпиляного під певним кутом і склеєного канадським бальзамом – прозорою ізотропною органічною речовиною з показником заломлення nб = 1,550. Отже, показник заломлення канадського бальзаму має проміжне значення між звичайним і незвичайним показниками заломлення ісландського шпату:
Таку призму виготовляють із ісландського шпату, розпиляного під певним кутом і склеєного канадським бальзамом – прозорою ізотропною органічною речовиною з показником заломлення nб = 1,550. Отже, показник заломлення канадського бальзаму має проміжне значення між звичайним і незвичайним показниками заломлення ісландського шпату: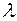 ), n (
), n (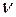 ),
),  (
(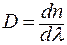 . (5.1.22)
. (5.1.22)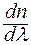 < 0). Характерна для різних прозорих матеріалів залежність показника заломлення світла від довжини хвилі – це монотонне зменшення n при зростаннідовжини світла. Тому для фіолетового світла (найменша довжина світла) будемо мати найбільший показник заломлення, а для червоного – найменший.
< 0). Характерна для різних прозорих матеріалів залежність показника заломлення світла від довжини хвилі – це монотонне зменшення n при зростаннідовжини світла. Тому для фіолетового світла (найменша довжина світла) будемо мати найбільший показник заломлення, а для червоного – найменший.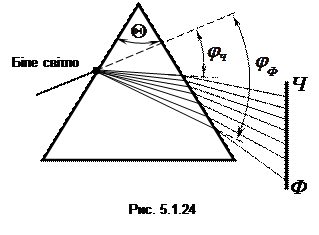 Астрономічні дослідження свідчать про те, що міжзоряний простір можна вважати вакуумом. Якби дисперсія в міжзоряному просторі існувала, то це проявилось би, наприклад, при спостереженні затемнень подвійних зірок. Такі спостереження ведуться вже більш ніж два століття. На початку затемнення колір зірки змінювався б від нормального в сторону до фіолетового, бо відповідне світло поширювалось би в просторі з найменшою швидкістю. В кінці затемнення колір змінювався б від червоного до нормального, бо швидкість червоного світла найбільша. Те, що таких ефектів не спостерігається свідчить про відсутність дисперсії в міжзоряному просторі, який можна вважати вакуумом.
Астрономічні дослідження свідчать про те, що міжзоряний простір можна вважати вакуумом. Якби дисперсія в міжзоряному просторі існувала, то це проявилось би, наприклад, при спостереженні затемнень подвійних зірок. Такі спостереження ведуться вже більш ніж два століття. На початку затемнення колір зірки змінювався б від нормального в сторону до фіолетового, бо відповідне світло поширювалось би в просторі з найменшою швидкістю. В кінці затемнення колір змінювався б від червоного до нормального, бо швидкість червоного світла найбільша. Те, що таких ефектів не спостерігається свідчить про відсутність дисперсії в міжзоряному просторі, який можна вважати вакуумом.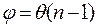 , (див. приклад розвязування задачі в п. 5.3., де отримано це співвідношення), то для фіолетового променя відхилення після проходження призми буде найбільшим, а для червоного – найменшим (рис. 5.1.24). Такий дослід був проведений ще Ньютоном, який вперше спостерігав розкладення білого світла в спектр. Всі інші промені будуть лежати між цими крайніми і створять спектр білого світла (райдуга), тобто випромінювання буде розкладено по довжинах хвиль.
, (див. приклад розвязування задачі в п. 5.3., де отримано це співвідношення), то для фіолетового променя відхилення після проходження призми буде найбільшим, а для червоного – найменшим (рис. 5.1.24). Такий дослід був проведений ще Ньютоном, який вперше спостерігав розкладення білого світла в спектр. Всі інші промені будуть лежати між цими крайніми і створять спектр білого світла (райдуга), тобто випромінювання буде розкладено по довжинах хвиль.


