
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад виконання варіанта 2 завдання ДТ2Содержание книги
Поиск на нашем сайте
Важке тіло D масою т рухається вздовж трубки АВС рис. Д.2´. На вертикальному відрізку АВ трубки на тіло D діють сила ваги
Розв’язання. Рух тіла D будемо розглядати окремо як прямолінійний рух матеріальної точки на відрізках АВ і ВС. 1. Розглянемо рух матеріальної точки на відрізку АВ. Покажемо тіло D у довільної точці ділянки АВ і діючи на нього сили
або, враховуючи що
Знаходимо, що Pz=P; Враховуючи, що Vt=V, маємо
Позначимо для спрощення: g= 10 м/с2; При цьому рівняння (2) приймає вигляд
Розділимо в (4) змінні і зінтегруємо обидві частини невизначеним інтегралом:
За початковими умовами при z =0; V=V0 маємо:
Звідси
Після відповідних перетворень маємо
Якщо в (6) підставимо z=l=2,5 м і к, п з (3), визначимо швидкість VB тіла в точці В (V0= 5 м/с, число е =2,7)
2. Розглянемо рух на відрізку ВС з початковою швидкістю V0=VB. Покажемо на цьому відрізку тіло D у довільної точці і діючи на нього сили
або
де рівняння (8) приймає вигляд:
Після скорочення на m знайдемо значення
або
Проінтегруємо це рівняння невизначеним інтегралом і знайдемо:
Враховуючи, що тіло знаходиться в точці В при t= 0 будемо мати початкову умову при t= 0 V=V0=VB, де VB відоме з рівності (7). При цьому з (11) одержимо
При С2 =8,4 рівняння (11) має вигляд:
Після інтегрування цього рівняння знаходимо:
Але при t =0 x= 0 і отже в (13) С3 =0. Тому остаточно маємо рівняння руху тіла на відрізку ВС:
де х – в метрах, t – в секундах.
Відповідь:
Завдання ДС. ДИНАМІКА МЕХАНІЧНОЇ СИСТЕМИ
Дослідження дінаміки руху системи матеріальних точок проводяться комплексно, шляхом використання різних методів для визначення основних характеристик руху конкретної механічної системи абсолютно твердих тіл під дією постійних сил ваги. Такий підхід дозволяє, крім тривіального надання навиків використання теорії для практичних розрахунків та їх закріплення, розв’язати також дуже важливу проблему аналізу одержаних різними методами результатів розв'язку однієї задачі динаміки. Це дає можливість порівняти різні шляхи розв'язання однієї задачі і перевірити правильність отриманих результатів.
Умови завдань ДС
Механічна система (механізм), яка складена з декількох абсолютно твердих тіл, починає рухатися з стану спокою під дією сил ваги. Вважаючи в'язі ідеальними і нехтуючи їх масами визначити в мить часу, коли тіло А пройде шлях S, величини які вказані в залежності від шифру в задачах 1, 2, 3,4, 5, 6, 7 завдання ДС. Схеми варіантів механічної системи показані на рис. 8. В завданні прийняті наступні позначення: mA, mB, mБ, mД - маси тіл А, В, Б, Д; Rв=2rв, RД=1,5rД - радіуси великих і малих кіл; івх, ідх - радіуси інерції тіл В і Д, відносно горизонтальних осей, що проходять через їх центри мас, a, b - кути нахилу площин до горизонту; m - коефіцієнт тертя тіла А. Необхідні дані наведено в таблиці 10. Таблиця 10
Рисунок 8
Завдання ДС1. Знайти швидкість тіла А даної механічної системи за допомогою теореми про зміну кінетичної енергії. Умови задачі наведено в завданні ДС.
Необхідно знати: 1. Теорему про зміну кінетичної енергії механічної системи. 2. Формули, за якими визначається кінетична енергія при поступальному, обертальному і плоскому рухах твердого тіла. 3. Формули, за якими визначається робота постійної сили, змінної сили, сили тертя, сили ваги, моменту сили. Необхідно вміти: 1. Визначати рухи твердого тіла. 2. Виконувати кінематичний розрахунок системи: за заданою швидкістю (прискоренням, переміщенням) даного тіла визначити швидкість (прискорення, переміщення) всіх об'єктів та точок, що складають систему твердих тіл. 3. Вираховувати кінетичну енергію конкретних твердих тіл, які складають механічну систему, в залежності від їх руху. 4. Вираховувати роботу конкретних сил, прикладених до тіл механічної системи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.69.101 (0.007 с.) |

 і сила опору R. Відстань від точки А, де V=V0, до точки В дорівнює l. На похилому відрізку ВС трубки на тіло діють сила ваги
і сила опору R. Відстань від точки А, де V=V0, до точки В дорівнює l. На похилому відрізку ВС трубки на тіло діють сила ваги  . Знайти рівняння руху тіла на відрізку ВС.
. Знайти рівняння руху тіла на відрізку ВС.

 V0 =5
V0 =5  l =2,5
l =2,5 
 Н
Н

 Рис.
Рис. 
 . Проведемо вісь Аz і складемо диференціальне рівняння руху точки D в проекціях на цю вісь:
. Проведемо вісь Аz і складемо диференціальне рівняння руху точки D в проекціях на цю вісь: ,
, ,
, . (1)
. (1)
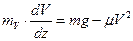 , або
, або  . (2)
. (2) 0,2 м-1;
0,2 м-1;  50 м2/с2 (3)
50 м2/с2 (3) (4)
(4)
 (5)
(5) із (5) знаходимо
із (5) знаходимо  , або
, або 
 ;
;  .
. . (6)
. (6) і
і  (7)
(7)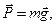

 і
і  (рис. Д.2´) проведемо з початком у точці В осі координат Ву і Вх і складемо диференціальне рівняння руху тіла в проекції на вісь В х:
(рис. Д.2´) проведемо з початком у точці В осі координат Ву і Вх і складемо диференціальне рівняння руху тіла в проекції на вісь В х:
 (8)
(8)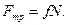 Для визначення N складемо рівняння руху в проекції на вісь Ву. Тому що ау= 0 одержимо
Для визначення N складемо рівняння руху в проекції на вісь Ву. Тому що ау= 0 одержимо  звідки
звідки  Отже
Отже  Крім того
Крім того  і
і (9)
(9) і 16/ т =8. Підставимо ці значення в (9) і матимемо
і 16/ т =8. Підставимо ці значення в (9) і матимемо , (10)
, (10) .
. (11)
(11)
 (12)
(12) (13)
(13)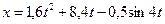 ,
,



