
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад виконання завдання К4
Прямокутний трикутник АВС обертається навколо свого катета АС рівносповільнено з кутовим прискоренням
ε=2с-2 S=20-5(cosπt/16)см t1=4с
Розв’язання
Оскільки точка М одночасно перебуває в двох рухах, то її рух розглядаємо як складний. Виберемо нерухому Oxyz і рухому O1x1y1z1 системи координат (рис. К.5). Рухома система зв’язана з трикутником що обертається (на рис. К.5 показана тільки вісь O1x1). Тоді переносним рухом буде обертання трикутника навколо катета АС, а відносним – прямолінійний рух точки вздовж катета АВ за законом S=S(t). Абсолютна швидкість точки М визначиться за формулою Переносну швидкість точки М визначимо як швидкість тієї точки гіпотенузи АВ трикутника, що обертається, з якою в даний момент часу співпадає рухома точка М. Визначимо положення точки М на гіпотенузі АВ при t = 4 с.
Переносна швидкість Ve=ωeh, де ωe - кутова швидкість обертання трикутника АВС при t= 4 с; h - найкоротша віддаль від точки М до осі обертання АС. При t = 4 с h=AMsin300=8,23 см. Оскільки обертання трикутника рівносповільнене, то ωe визначимо за залежністю ωe=ω0-εet і при t = 4 с ωe=4 c-1. Тоді Ve=4×8,23=32,92 см/с. Оскільки траєкторією переносного руху точки М в даний момент часу є коло радіуса h, то вектор Вектор
При непоступальному переносному русі абсолютне прискорення точки М в складному русі буде дорівнювати Оскільки переносний рух є обертальним, то переносне прискорення точки М визначиться за формулою: де
Вектор
При прямолінійному відносному русі, відносне прискорення точки М має тільки дотичну складову, яка дорівнює
Вектори Модуль коріолісового прискорення визначиться за залежністю
Згідно з прийнятим напрямком обертання вектор
Напрям вектора Для знаходження модуля абсолютного прискорення точки М скористаємося методом проекцій. Для цього введемо допоміжну систему координат Mx2y2z2, осі якої напрямлені відповідно по дотичній до переносної траєкторії, по радіусу h і паралельно до осі обертання (рис. К.6). Отже,
Модуль абсолютного прискорення точки М
Відповідь: V а =32,9 см/с; аа =132,3 см/с2.
Розділ II. СТАТИКА Завдання С. Статика Завдання С1. ПЛОСКА СИСТЕМА СИЛ. Визначення реакцій в’язей. Визначити реакції в’язей для трьох випадків закріплення бруса, віссю якого є ламана лінія. Задане навантаження (див. табл.5’) і розміри (м) в усіх трьох випадках однакові. Схеми конструкцій показані на рис. 4, а необхідні данні наведенні в таблиці 5.
Необхідно знати: 1. Рівняння рівноваги плоскої системи сил. 2. Момент сили відносно точки. 3. Момент сил пари відносно точки дорівнює моменту самій пари. Необхідно вміти: 1.Визначати момент сили відносно точки. 2.Визначати момент пари сил.
Приклад виконання завдання С1 На брус з ломаною віссю АВ (рис. 2.1) діють пари сил, момент якої дорівнює М, рівномірно розподілене навантаження інтенсивності q, а в точці D прикладена зосереджена сила
Розв’язання
Задачу розв’язуємо у слідуючій послідовності: 1. За умовою задачі виділяємо тіло, рівновага якого розглядається і показуємо його окремо. Згідно з умовою задачі тілом, рівновага якого розглядається, є брус з ломаною віссю АВ (рис. С.2). 2. Покажемо на рис. С.2 діючи на цей брус задані активні сили і реакції відкинутих в’язей. Активними силами є зосереджена сила Дію рівномірного розподіленого навантаження інтенсивності q заміняємо дією рівнодійної сили
В’язями, накладеними на брус АВ, є опори у вигляді циліндричного шарніра А, дію якого замінемо реакцією Система заданих активних сил
Рис. С.2
3. На брус АВ діє плоска довільна система сил, рівняння рівноваги якої
1. 2. 3. З цієї системи рівнянь дістанемо
з рівняння 1 з рівняння 2 з рівняння 3
Відповідь: Завдання С2. ПРОСТОРОВА СИСТЕМА СИЛ. Визначення реакцій в’язей і умов рівноваги невільного твердого тіла. Знайти реакції в’язей (опор) заданої просторової конструкції і умову її рівноваги. Схеми конструкцій показані на рис 5, а необхідні дані наведені в таблиці 5.
Необхідно знати: 1. Рівняння рівноваги довільної просторової системи сил. 2. Обчислювати момент сили відносно осі Необхідно вміти: 1. Дію в’язей заміняти дією їх реакцій. 2. Проецюювати вектор сили на координатні осі. 3. Визначати моменти сили відносно осей координат.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.0.53 (0.024 с.) |
 , при початковій кутовій швидкості ω0=12 с-1. По гіпотенузі АВ рухається точка М за законом АМ=S=20-5cos(πt/16) (S - в сантиметрах, t - в секундах). Знайти абсолютну швидкість і абсолютне прискорення точки М в момент часу t1=4 с (рис. К.5).
, при початковій кутовій швидкості ω0=12 с-1. По гіпотенузі АВ рухається точка М за законом АМ=S=20-5cos(πt/16) (S - в сантиметрах, t - в секундах). Знайти абсолютну швидкість і абсолютне прискорення точки М в момент часу t1=4 с (рис. К.5).
 Рис К.6
Рис К.6
 Дано:
Дано:
 ω0=12 с-1
ω0=12 с-1 Va -? аa -?
Va -? аa -? .
. .
. буде напрямлений по дотичній до цього кола в сторону обертання. Якщо площину трикутника АВС при t = 4 с сумістити з площиною OYZ, то вектор
буде напрямлений по дотичній до цього кола в сторону обертання. Якщо площину трикутника АВС при t = 4 с сумістити з площиною OYZ, то вектор  . Відносна швидкість точки М визначиться методами кінематики точки і буде дорівнювати
. Відносна швидкість точки М визначиться методами кінематики точки і буде дорівнювати  і при t = 4 с; Vr = 0,69 см/с.
і при t = 4 с; Vr = 0,69 см/с.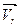 напрямлений по гіпотенузі АВ в сторону збільшення S. Оскільки кут між векторами
напрямлений по гіпотенузі АВ в сторону збільшення S. Оскільки кут між векторами  .
. .
.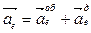 ,
, ; при t = 4 с
; при t = 4 с  ,
, .
.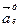 напрямлений до осі обертання трикутника вздовж радіуса h, а вектор
напрямлений до осі обертання трикутника вздовж радіуса h, а вектор  - перпендикулярно до
- перпендикулярно до  в сторону дугової стрілки кутового прискорення εe, яке протилежне ωe так як обертання сповільнене.
в сторону дугової стрілки кутового прискорення εe, яке протилежне ωe так як обертання сповільнене. . При t = 4 с, ar =
. При t = 4 с, ar =  = 0,14 см/с2.
= 0,14 см/с2. мають при t = 4 с однакові знаки і тому співпадають за напрямком.
мають при t = 4 с однакові знаки і тому співпадають за напрямком. .
. буде напрямлений по осі обертання в сторону додатнього напрямку осі oz. Тому кут між
буде напрямлений по осі обертання в сторону додатнього напрямку осі oz. Тому кут між  .
. , згідно з правилом Жуковського, співпадає з напрямом вектора
, згідно з правилом Жуковського, співпадає з напрямом вектора  ;
; ;
; .
. .
. . Визначити реакції опор, якщо М =8 кН . м; q =1,2 кН/м; Р= 5 кН. Розміри та кут
. Визначити реакції опор, якщо М =8 кН . м; q =1,2 кН/м; Р= 5 кН. Розміри та кут  показані на рис. С.1.
показані на рис. С.1.
 кН.
кН. і реактивним моментом МА, і рухомого шарніра, дію якого замінимо реакцією
і реактивним моментом МА, і рухомого шарніра, дію якого замінимо реакцією 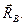
 , пара сил з моментом М і невідомі реакції в’язей
, пара сил з моментом М і невідомі реакції в’язей  і реактивний момент
і реактивний момент  , складають зрівноважену довільну плоску систему сил, показану на рис. С.2.
, складають зрівноважену довільну плоску систему сил, показану на рис. С.2.
 ;
; 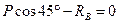
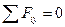 ;
; 
 ;
; 
 ;
; ;
; .
.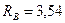 кН;
кН;  кН;
кН;  кН . м.
кН . м.


