
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад виконання завдання К2Содержание книги Поиск на нашем сайте
За заданим рівнянням прямолінійного руху вантажу 1 визначити швидкість, обертальне, доцентрове і повне прискорення точки М механізму (рис.К.2) в той момент часу, коли шлях, пройдений вантажем, дорівнює S=0,3 м. Дано: R2=30 см, r2=15 см, R3=40 см, r3=20 см, x=90t2 см. Розв’язання. Тіло 1 здійснює поступальний рух, а тіла 2 і 3 – обертальні рухи. Знайдемо швидкість вантажу 1 (рис. К.2) Оскільки трос нерозтяжний, то швидкість точки К колеса 2 дорівнює швидкості вантажу V1. Тоді, кутова швидкість тіла 2 визначиться за формулою
Кутову швидкість колеса 3 знайдемо за співвідношенням
Кутове прискорення тіла 3 визначимо за формулою
Рис К.2 Рис К.2'
Швидкість точки М дорівнює
Вектор швидкості Обертальне
Вектор обертального прискорення
Повне прискорення точки визначимо за формулою
Визначимо момент часу τ, коли шлях S, пройдений вантажем 1, дорівнює 30 см: Звідки
Значення всіх кінематичних характеристик руху точки М для моменту часу Відповідь:
Вектори швидкості і прискорень точки М показані на рис. К.2'. Завдання К3. ВИЗНАЧЕННЯ ОСНОВНИХ КІНЕМАТИЧНИХ ХАРАКТЕРИСТИК ПЛОСКОГО РУХУ ТВЕРДОГО ТІЛА. КІНЕМАТИЧНИЙ АНАЛІЗ ПЛОСКОГО МЕХАНІЗМУ. Для заданого положення механізму знайти швидкість точки С і прискорення точки В, а також кутову швидкість і кутове прискорення ланки, яка робить плоский рух. Схеми механізмів показані на рис. 2, необхідні дані наведені в таблиці 3.
Необхідно знати: 1. Формулу, що визначає швидкість точки М твердого тіла, яке робить плоский рух. 2. Поняття миттєвого центру швидкостей (м.ц.ш.). 3. Теорему про проекції швидкостей двох точок плоскої фігури. 4. Теорему про прискорення точок плоскої фігури. Необхідно вміти: 1. Класифікувати рухи ланок плоского механізму. 2. Визначати положення миттєвого центру швидкостей ланки, що робить плоский рух, як м.ц.ш. плоскої фігури. 3. Використовувати поняття м.ц.ш. для визначення швидкостей точок плоскої фігури. 4. Аналітичне додавати вектори і визначати їх суму.
Приклад виконання завдання К3 Знайти швидкість точки В і прискорення точок В і Р рухомої шестерні радіуса r=0,05 м., яка котиться в середині нерухомої шестерні радіуса R=0,15 м. Шестерню радіуса r рухає кривошип, який обертається навколо осі О рівномірно з кутовою швидкістю
R=0,15 м r=0,05 м
ОА=0,1м
Розв’язання 1. Аналіз руху механізму. Досліджуючи рух механізму бачимо, що кривошип ОА, рівномірно обертаючись навколо осі О, рухає шестерню, яка в свою чергу обертається навколо пальця кривошипу А. Рухома шестерня котиться в середині нерухомої шестерні без ковзання. Отже, рух малої шестерні є плоскопаралельний, а рух кривошипа обертальний навколо нерухомої осі. 2. Визначення швидкості точки В. Положення миттєвого центра швидкостей малої шестерні Р відоме за умовою і тому її плоский рух в даний момент часу можна розглядати як обертальний навколо миттєвого центра швидкостей Р (рис.К.4).
Рис К.4
Отже за законами розподілу швидкостей відносно миттєвого центра швидкостей дістанемо
Звідки
Невідому швидкість точки А, можна знайти як швидкість точки кривошипа ОА:
Вектор
3. Визначення прискорень точок В і Р. Плоский рух малої шестерні складається з поступального руху разом з полюсом, точкою А, і обертальною навколо осі, що проходить через полюс А. Прискорення точок В і Р визначимо за теоремою про додавання прискорень у плоскому русі:
де за модулем:
Спочатку визначимо прискорення полюса, точки А, як точки кривошипа ОА. Кривошип ОА обертається навколо осі О з сталою кутовою швидкістю. Отже, його кутове прискорення дорівнює нулю:
і напрямлене до центра обертання кривошипа О по радіусу ОА. Визначимо кутову швидкість Миттєвий центр швидкостей знаходиться в точці Р, отже:
За умовою задачі
Вектори Вектори Таким чином, прискорення точок В і Р знаходиться за формулами
Як показано на рис.К.4, вектори прискорень
а вектори прискорень
Відповідь: Завдання К4. СКЛАДНИЙ РУХ ТОЧКИ. Визначення абсолютної швидкості і абсолютного прискорення точки. За данними рівняннями відносного руху точки М і переносного руху тіла Д визначити для моменту часу t=t1 абсолютну швидкість і абсолютне прискорення точки М, яка починає рухатися з точки О. На схемах механізмів точка М показана довільно. Схеми механізмів показані на рис. З, а необхідні дані наведено в таблиці 4.
Необхідно знати: 1. Основні визначення складного руху точки: - абсолютний, відносний і переносний рухи; - абсолютна - абсолютне - прискорення Коріоліса 2. Як визначається абсолютна швидкість точки. 3. Як визначається абсолютне прискорення точки. 4. Як визначається напрямок прискорення Коріоліса за правилом Жуковського. Необхідно вміти: 1. Складний рух точки розкладати на відносний та переносний. 2. Брати похідні від простих функцій. 3. Знаходити напрямок прискорення Коріоліса. 4. Визначати вектор, що дорівнює векторній сумі декількох векторів.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.178.122 (0.007 с.) |

 .
. .
. . Звідси
. Звідси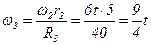 .
. .
.
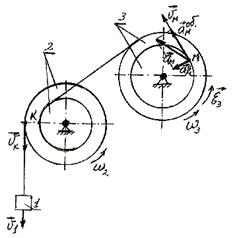
 .
. напрямлений перпендикулярно до радіуса r3 в сторону обертання колеса 3 (рис. К.2').
напрямлений перпендикулярно до радіуса r3 в сторону обертання колеса 3 (рис. К.2'). і доосьове
і доосьове  прискорення точки М визначимо за формулами
прискорення точки М визначимо за формулами
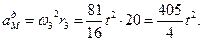
 співпадає за напрямом з вектором швидкості
співпадає за напрямом з вектором швидкості 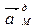 напрямлений по радіусу від точки М до центра колеса 3.
напрямлений по радіусу від точки М до центра колеса 3. .
.

 =0,58 c будуть відповідними:
=0,58 c будуть відповідними:  ;
;  ;
;  ;
;  .
. см/с;
см/с;  см/с;
см/с;  см/с.
см/с. 
 =3 рад/с (рис. К.3).
=3 рад/с (рис. К.3). Рис. К.3.
Рис. К.3.
 Дано:
Дано:
 -?
-? -?
-? -?
-?

 (1)
(1) м/с
м/с напрямлений перпендикулярно до ОА, а вектор М – перпендикулярно до ВР (рис.К.4). Модуль вектора
напрямлений перпендикулярно до ОА, а вектор М – перпендикулярно до ВР (рис.К.4). Модуль вектора  знаходимо за формулою (1):
знаходимо за формулою (1):

 ,
, r;
r;  r. (2)
r. (2)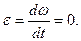 Прискорення точки А кривошипа визначаються за формулою:
Прискорення точки А кривошипа визначаються за формулою:  де за модулем:
де за модулем: 
 . Отже, прискорення точки А дорівнює:
. Отже, прискорення точки А дорівнює:
 і кутове прискорення
і кутове прискорення  рухомої шестерні, необхідні для формул (2).
рухомої шестерні, необхідні для формул (2).
 , тому що
, тому що  Таким чином згідно (2) модулі прискорень
Таким чином згідно (2) модулі прискорень  і
і 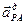 дорівнюють:
дорівнюють:
 і
і  дорівнюють нулю, згідно формули (2), тому, що
дорівнюють нулю, згідно формули (2), тому, що 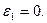

 (3)
(3) і
і  ,
,



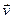 , відносна
, відносна  і переносна
і переносна  швидкості точки;
швидкості точки; , відносне
, відносне  , і переносне
, і переносне  прискорення точки;
прискорення точки; .
.


