
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні правила комбінаторикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Комбінаторика має справу із скінченими множинами і виникла як одна із теорій ігор. Правило сум Розглянемо потужність об’єднання двох множин
Якщо А і В є підмножинами множини С. так що
Формуліровка: Якщо деякий об’єкт х Правило сум може бути застосовано і для більшої ніж 2 кількості множин. Правило добутку Нехай нам необхідно розрахувати кількість пар (а Якщо Формуліровка: Якщо об’єкт а У деяких випадках необхідно обчислити число всеможливих способів вибрати впорядковані вибірки Розміщення. Приклад 1. Колесо велосипедиста після падіння має вигляд 8. Оскільки хазяїн Клубу – велосипедист, то здійснюється нову нумерація усіх квитків так, щоб число 8 у них не входило. Відомо, що число членів клубу тризначне число (як виявилось). Скільки членів клубу? Якщо допускається номер 0.0.0. (Розв’язок Приклад 2: Система числення В «n» – мірні системі числення використовується “n” чисел. Скільки можна записати чисел, які записується “К” знаками.
Одним з прикладів не рівномірного коду є Код Морзе. У ньому використовуються всього 2 символи: крапка та тире.
Однак довжина кодового слова різна. Приклад 3 Яке найменше число знаків “∙” чи “–” повинна містити комбінація, щоб можна було передати довільну букву при використанні рівномірного коду? Виявляється, що 5. Чому? Одно позиційне число дає можливість передати лише 2 різні сигнали. Двох позиційні - “4”. 3х позиційні - “8”. 4х позиційні “16”, це менше ніж вміст алфавіту української мови (30). Тому телеграфний код, код Бодо, містить 5ти - символьне слово – код, для передачі тексту. Аналогічно можна розглянути спосіб обчислення об’єму алфавіту кодів для морського семафору, що містить комбінації- таких варіантів кодів цілком достатньо для передачі усіх букв. (Усіх 33.) Приклад 4. Генетичний код. Наслідкова інформація записується з допомогою різних порядків
Як же природа використовує даний надлишок коду невідомо? Розміщення, перестановки і сполуки без повторень. З допомогою загальних правил комбінаторики можна розв’язувати різні задачі, при цьому виникають строго певні комбінації, яким присвоєно імена: розміщення, перестановки сполучення (комбінації). Означення. Скінчена множина називається впорядкованою, якщо кожному її елементу ставиться у відповідність натуральне число “к”, яке означає порядковий номер елементу в множині А де Розглянемо підмножини 1) Перший крок 2) Із множини 3) Із множини 4) Із множини Із вибраних елементів складаємо
Позначається вибірка Якщо ж вибірку елементів брати з повної множини A весь час, то частина елементів буде повторюватись і Приклад з білетами, коли білет вибраний студентом вилучається (реалізується вибірка без повторів) і коли не вилучається – вибірка з повторами. Означення 2. Розміщення з “n” по “к” називається впорядкована “к” вибірка без повторення із множини А, для якої Доведення. Переконаємось (див. кодіровку без повторень) в вірності співвідношення приведеного співвідношення. На першому місці можна встановити один із “n” елементів множини, на другому – один із “n-1 “ елементів, що залишились.
Тому, очевидно, що
Означення 3. “ n” перестановкою називається впорядкована n-мірна вибірка без повторень із множини А, причому
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.216 (0.007 с.) |


 при чому
при чому  , тобто кожен із об’єктів входить лише в одну множину. Тоді
, тобто кожен із об’єктів входить лише в одну множину. Тоді

 А можна вибрати “n” способами, а другий об’єкт у
А можна вибрати “n” способами, а другий об’єкт у  .)
.) в
в  ) таких що а
) таких що а 
 і т.д. ця кількість буде
і т.д. ця кількість буде 

 можна здійснити
можна здійснити  де
де 
 і т.д.
і т.д. 
 . Якщо потужність множин
. Якщо потужність множин  …,
…,  то загальна кількість можливих варіантів здійснення вибірки буде
то загальна кількість можливих варіантів здійснення вибірки буде 


 . Використання тільки “n” чисел для кодування інформації приводить до так званих рівномірних кодів.
. Використання тільки “n” чисел для кодування інформації приводить до так званих рівномірних кодів.

 азотистих основ: аденін, тіамін, гуанін, цітазин. Ці основи встановлюють порядок будови білків організму із амінокислот, яких кількість порядку 20. Причому кожна амінокислота кодується з допомогою 3х чисел. Чому?
азотистих основ: аденін, тіамін, гуанін, цітазин. Ці основи встановлюють порядок будови білків організму із амінокислот, яких кількість порядку 20. Причому кожна амінокислота кодується з допомогою 3х чисел. Чому? не досить для побудови усіх необхідних білків.
не досить для побудови усіх необхідних білків. досить з надлишком для створення усіх білків.
досить з надлишком для створення усіх білків. де
де 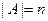 . Якщо порядок елементів неістотній, то множина називається невпорядкованою.
. Якщо порядок елементів неістотній, то множина називається невпорядкованою. , які утворюються за слідуючим правилом:
, які утворюються за слідуючим правилом: вибираємо будь-який елемент
вибираємо будь-який елемент 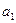 ; із множини А
; із множини А вибираємо
вибираємо 
 вибираємо
вибираємо 
 вибираємо
вибираємо 

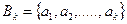 - це буде вибірка без повторень, вона впорядкована, якщо кожному вибраному елементу множини
- це буде вибірка без повторень, вона впорядкована, якщо кожному вибраному елементу множини  поставити у відповідність номер. Отримали впорядковану k вибірку без повторів. А якщо елементам множини
поставити у відповідність номер. Отримали впорядковану k вибірку без повторів. А якщо елементам множини  .
. . Загальна кількість різних розміщень позначається
. Загальна кількість різних розміщень позначається  .
.
 - згідно правила добутку. Даний вираз можна переписати у вигляді
- згідно правила добутку. Даний вираз можна переписати у вигляді де
де 
 ;
;  , зручному для користування.
, зручному для користування. .Ясно, що будь-які n -перестановки відрізняються лише порядком елементів, і кожна вибірка містить усі елементи множини А.
.Ясно, що будь-які n -перестановки відрізняються лише порядком елементів, і кожна вибірка містить усі елементи множини А.


