
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пояснення методики обчислення на іншому прикладі. ⇐ ПредыдущаяСтр 4 из 4
4 ящики - 6 елементів. 3-й ящик порожній
Дане, конкретне, розміщення описується кодом-вибіркою 111011001. Тоді, обчислюючи кількість перестановок елементів у вибірці з повторами За допомогою даного методу визначається кількість можливих розміщень. Якщо ж необхідно визначити кількість різних варіантів, за умовою, щоб в кожному було обов’язково по одному предмету, то спочатку розкладемо по одному предмету в кожний ящик. Залишиться n –m об’єктів, які необхідно додатково розмістити по ящиках. Загальна кількість варіантів буде Сполуки (комбінації) з повторенням. Сполукою із n по к з повторенням називається невпорядкована к -вибірка з повторенням із множини А для якої Приклади сполук з повторами. Для множини Якщо сполуки були отримані з множини
1 0 0 1 …01 одиничок “к”, нулів n-1. Тоді, обчисливши вираз
Якщо в сполуки з повтореннями обов‘язково повинні входити “r” фіксованих типів елементів, то спочатку їх заповнимо. Залишається n – r елементів, які необхідно розподілити по k коробках. Маємо Біном Ньютона. Властивості біноміальних коефіцієнтів. Розглянемо степені двохчлена Числа Фібоначі, ряд Фібоначі, трикутник Паскаля.
121 1331 14641 15101051 і т. д. Тоді Властивості розкладу бінома Ньютона та біноміальних коефіцієнтів.
1. Кількість доданків у розкладі 2. У кожному доданку сума показників рівна “n”, що - відповідає загальній розмірності елементів лівої частини. 3. Загальний член розкладу 4. Коефіцієнти розкладу, рівновіддалені від його кінців, рівні між собою бо 5. Середній член розкладу при n=2р (парному) найбільший якщо ж n=2р-1 (відсутній один, середній член) то найбільших доданків два однакових. 6. Сума усіх біноміальних коефіцієнтів Доведемо. При 7. Сума біноміальних коефіцієнтів з парними k рівна сумі значень Дійсно, якщо взяти Тоді Ряд Ньютона! Повернемось до бінома Ньютона, який дає можливість записати вираз Саме він показав, що, якщо “а” додатне число і
Тобто, в цьому випадку ряд буде безмежним. Тільки при цілих Розглянемо два практичних випадки реалізації. 1. По іншому дану формулу можна переписати у виді
причому Це співвідношення можна довести методом індукції (самостійно Комбінаторика Н.Я. Виленкин ст..200.) 2. Розглянемо алгоритм обчислення квадратних коренів із заданих чисел, тобто у випадку коли
Цей вираз можна використати при обчисленнях кореня квадратного з раціональних чисел з любою точністю. Для цього досить винести з під кореня найбільше число, корінь якого відомий.
Наприклад.
Перетворивши останній вираз, отримаємо
Це можна здійснити також і наступним способом
104 4 416 1087 7 7609 79100 і т.д.
От чому розклад
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.01 с.) |
 0
0  0
0  0
0 
 визначаємо число можливих розміщень n елементів по m ящиках.
визначаємо число можливих розміщень n елементів по m ящиках. . Прикладом такого методу розміщення може служити телевізійний сигнал. І біт визначає початок нового кадру. Або ж, при зв’язку через послідовний порт, існують при кожній посилці стартові та стопові біти.
. Прикладом такого методу розміщення може служити телевізійний сигнал. І біт визначає початок нового кадру. Або ж, при зв’язку через послідовний порт, існують при кожній посилці стартові та стопові біти.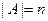 . Кількість сполук позначається
. Кількість сполук позначається  .
. можна створити сполуки
можна створити сполуки  і т.д. Для отримання формули, яка визначає кількість різних сполук скористаємось кодуванням, яке було розглянуто раніше.
і т.д. Для отримання формули, яка визначає кількість різних сполук скористаємось кодуванням, яке було розглянуто раніше. , то маємо елементи “n” типів. Кожній сполуці із n по к відповідає її код-перестановка з повторами яка містить k -одиницьта n-1 – нулів (дійсно нулі розміщаються лише між елементами
, то маємо елементи “n” типів. Кожній сполуці із n по к відповідає її код-перестановка з повторами яка містить k -одиницьта n-1 – нулів (дійсно нулі розміщаються лише між елементами  , тому їх буде на 1 менше ніж груп). Один із прикладів розміщення
, тому їх буде на 1 менше ніж груп). Один із прикладів розміщення
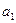

 ….
…. 

 отримаємо загальну кількість відповідних сполук. Зауважимо, що способи розподілу “n” однакових елементів по m різних комірках – це задача на сполуки з повтореннями.
отримаємо загальну кількість відповідних сполук. Зауважимо, що способи розподілу “n” однакових елементів по m різних комірках – це задача на сполуки з повтореннями. 
 сполук.
сполук. де
де 

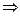

 к =0,1
к =0,1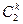 к =0,1,2
к =0,1,2 к =0,1,2,3
к =0,1,2,3 к=0,1,2,3,4
к=0,1,2,3,4 к = 0,1,2,3,4,5
к = 0,1,2,3,4,5 формула біному Ньютона.
формула біному Ньютона.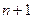
 .
.




 з непарними k. Тобто
з непарними k. Тобто  де
де  - ціла частина х.
- ціла частина х.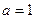 та
та 
 . Якщо перенести від‘ємні коефіцієнти направо то отримаємо необхідне співвідношення.
. Якщо перенести від‘ємні коефіцієнти направо то отримаємо необхідне співвідношення.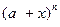 у вигляді розкладу по степеням а та х. Відмітимо, що дану формулу знали і до Ньютона (середньоазіатські вчені Омар Хайям, Гияседін та інші). В західній Європі до Ньютона її знав Паскаль. В чому ж заслуга Ньютона? В тому, що він розширив дану формулу на не цілі показники.
у вигляді розкладу по степеням а та х. Відмітимо, що дану формулу знали і до Ньютона (середньоазіатські вчені Омар Хайям, Гияседін та інші). В західній Європі до Ньютона її знав Паскаль. В чому ж заслуга Ньютона? В тому, що він розширив дану формулу на не цілі показники.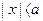 , то, для довільного дійсного значення
, то, для довільного дійсного значення  , має місце рівність
, має місце рівність
 в чисельнику буде момент, що появиться дужка
в чисельнику буде момент, що появиться дужка  =0: всі подальші члени розкладу пропадуть!
=0: всі подальші члени розкладу пропадуть!

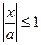 , адже
, адже 
 ;
;
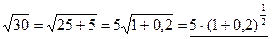 а дальше ряд Ньютона
а дальше ряд Ньютона дозволить обчислити значення з довільною, бажаною степеню точності.
дозволить обчислити значення з довільною, бажаною степеню точності.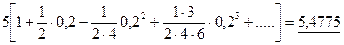 .
.
 500
500 в ряд по степенях b став називатись біномом Ньютона.
в ряд по степенях b став називатись біномом Ньютона.


