
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Комбінаторний аналіз.Содержание книги
Поиск на нашем сайте
Розділ 2. Комбінаторний аналіз. Вступ. При розв’язуванні практичних задач виникають випадки, коли розглядаються взємозв’язок, комбінації елементів деякої скінченої множини. Наприклад: скількома способами можна розсадити студентів по стільцях. Яка імовірність виграшу при заповненні однієї картки в “КЕНО” і т.д. Розділ математики, в якому вивчається питання про число всеможливих комбінацій, що задовольняють тим чи іншим умовам, називається комбінаторикою. Початок досліджень в даному розділі математики виконували в XVII ст. Тартальї, Паскаль, Ферма і в подальшому Бернулі, Лейбніц, Ейлер та інші. Це пов’язано в першу чергу із застосуванням комбінаторики в азартних іграх. За останні роки розвиток комбінаторики пов’язаний з розв’язуванням транспортних задач, складанням планів виробництва та реалізації продукції тощо. Комбінаторика використовується в задачах лінійного програмуванні, статистики, для складання та декодування шифрів, при оцінці складності алгоритмів розв’язування задач в теорії інформації. Загальні правила комбінаторики Комбінаторика має справу із скінченими множинами і виникла як одна із теорій ігор. Правило сум Розглянемо потужність об’єднання двох множин
Якщо А і В є підмножинами множини С. так що
Формуліровка: Якщо деякий об’єкт х Правило сум може бути застосовано і для більшої ніж 2 кількості множин. Правило добутку Нехай нам необхідно розрахувати кількість пар (а Якщо Формуліровка: Якщо об’єкт а У деяких випадках необхідно обчислити число всеможливих способів вибрати впорядковані вибірки Розміщення. Приклад 1. Колесо велосипедиста після падіння має вигляд 8. Оскільки хазяїн Клубу – велосипедист, то здійснюється нову нумерація усіх квитків так, щоб число 8 у них не входило. Відомо, що число членів клубу тризначне число (як виявилось). Скільки членів клубу? Якщо допускається номер 0.0.0. (Розв’язок Приклад 2: Система числення В «n» – мірні системі числення використовується “n” чисел. Скільки можна записати чисел, які записується “К” знаками.
Одним з прикладів не рівномірного коду є Код Морзе. У ньому використовуються всього 2 символи: крапка та тире.
Однак довжина кодового слова різна. Приклад 3 Яке найменше число знаків “∙” чи “–” повинна містити комбінація, щоб можна було передати довільну букву при використанні рівномірного коду? Виявляється, що 5. Чому? Одно позиційне число дає можливість передати лише 2 різні сигнали. Двох позиційні - “4”. 3х позиційні - “8”. 4х позиційні “16”, це менше ніж вміст алфавіту української мови (30). Тому телеграфний код, код Бодо, містить 5ти - символьне слово – код, для передачі тексту. Аналогічно можна розглянути спосіб обчислення об’єму алфавіту кодів для морського семафору, що містить комбінації- таких варіантів кодів цілком достатньо для передачі усіх букв. (Усіх 33.) Приклад 4. Генетичний код. Наслідкова інформація записується з допомогою різних порядків
Як же природа використовує даний надлишок коду невідомо? Означення. Скінчена множина називається впорядкованою, якщо кожному її елементу ставиться у відповідність натуральне число “к”, яке означає порядковий номер елементу в множині А де Розглянемо підмножини 1) Перший крок 2) Із множини 3) Із множини 4) Із множини Із вибраних елементів складаємо
Позначається вибірка Якщо ж вибірку елементів брати з повної множини A весь час, то частина елементів буде повторюватись і Приклад з білетами, коли білет вибраний студентом вилучається (реалізується вибірка без повторів) і коли не вилучається – вибірка з повторами. Означення 2. Розміщення з “n” по “к” називається впорядкована “к” вибірка без повторення із множини А, для якої Доведення. Переконаємось (див. кодіровку без повторень) в вірності співвідношення приведеного співвідношення. На першому місці можна встановити один із “n” елементів множини, на другому – один із “n-1 “ елементів, що залишились.
Тому, очевидно, що
Означення 3. “ n” перестановкою називається впорядкована n-мірна вибірка без повторень із множини А, причому Перестановки з повторенням. Раніше перестановки були різними, якщо переставлялись два елементи множини (бо вони різні). Оскільки у нас вибірки містять однакові елементи то, здійснюючи перестановку ми можемо мати повторення послідовності (якщо переставили однакові елементи). Раніше, коли елементи були різними, наприклад в слові мегаполіс 9 букв, довільні перестановки елементів приводили до зміни вибірки. В наведеному прикладі їх Ясно, що число перестановок Узагальнимо дане положення. Нехай для k різних типів предметів (елементів множини) необхідно обчислити кількість перестановок з елементів
Наприклад: (Сполука.) Нехай у нас є множина Тому Задача: Нехай в сигналі, який складається з кодового слова, що містить 18 кодових символів в трійковій системі числення є нулів -5; 1- 6; 2-7. Скільки різних кодових слів можна організувати з допомогою перестановки? Якщо б усі кодові символи були різними то їх кількість була б 18!. Оскільки маємо перестановки з повтореннями то їх буде значно менше в Задача 2. Скільки чотиризначних різних кодових послань можна здійснити передаючи числа із множини Якщо числа різні, то їх Якщо посилка містить 2 однакових числа, тоді їх кількість буде Повна кількість різних кодових комбінацій буде
Розглянемо задачу обчислення числа способів розташування n однакових предметів по m різних коробках. Для цього закодуємо кожен розподіл з допомогою “0” та 1 наступним чином. Кожен предмет позначаємо одиничкою. Границю ящика позначаємо 0, при цьому враховуємо лише границі поділу предметів. Наприклад. Обчислимо кількість роізних варіантів розміщення 12 предиетів по чотирьох ящиках. Приводимо один із можливих варіантів розміщення. Кількість предметів, що попали в І ящик 5,щоб відділити їх ставимо “0”. І так далі. Якщо ящик порожній, то на схемі будуть два нулі поруч (порожнім є 3-й ящик). В четвертому ящику є 1 елемент.
Повну кількість різних розміщень отримаємо перестановками Наприклад.
Перетворивши останній вираз, отримаємо
Це можна здійснити також і наступним способом
104 4 416 1087 7 7609 79100 і т.д.
От чому розклад
Розділ 2. Комбінаторний аналіз. Вступ. При розв’язуванні практичних задач виникають випадки, коли розглядаються взємозв’язок, комбінації елементів деякої скінченої множини. Наприклад: скількома способами можна розсадити студентів по стільцях. Яка імовірність виграшу при заповненні однієї картки в “КЕНО” і т.д. Розділ математики, в якому вивчається питання про число всеможливих комбінацій, що задовольняють тим чи іншим умовам, називається комбінаторикою. Початок досліджень в даному розділі математики виконували в XVII ст. Тартальї, Паскаль, Ферма і в подальшому Бернулі, Лейбніц, Ейлер та інші. Це пов’язано в першу чергу із застосуванням комбінаторики в азартних іграх. За останні роки розвиток комбінаторики пов’язаний з розв’язуванням транспортних задач, складанням планів виробництва та реалізації продукції тощо. Комбінаторика використовується в задачах лінійного програмуванні, статистики, для складання та декодування шифрів, при оцінці складності алгоритмів розв’язування задач в теорії інформації.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.140.232 (0.011 с.) |


 при чому
при чому  , тобто кожен із об’єктів входить лише в одну множину. Тоді
, тобто кожен із об’єктів входить лише в одну множину. Тоді

 А можна вибрати “n” способами, а другий об’єкт у
А можна вибрати “n” способами, а другий об’єкт у  .)
.) в
в  ) таких що а
) таких що а 
 і т.д. ця кількість буде
і т.д. ця кількість буде 

 можна здійснити
можна здійснити  де
де 
 і т.д.
і т.д. 
 . Якщо потужність множин
. Якщо потужність множин  …,
…,  то загальна кількість можливих варіантів здійснення вибірки буде
то загальна кількість можливих варіантів здійснення вибірки буде 


 . Використання тільки “n” чисел для кодування інформації приводить до так званих рівномірних кодів.
. Використання тільки “n” чисел для кодування інформації приводить до так званих рівномірних кодів.

 азотистих основ: аденін, тіамін, гуанін, цітазин. Ці основи встановлюють порядок будови білків організму із амінокислот, яких кількість порядку 20. Причому кожна амінокислота кодується з допомогою 3х чисел. Чому?
азотистих основ: аденін, тіамін, гуанін, цітазин. Ці основи встановлюють порядок будови білків організму із амінокислот, яких кількість порядку 20. Причому кожна амінокислота кодується з допомогою 3х чисел. Чому? не досить для побудови усіх необхідних білків.
не досить для побудови усіх необхідних білків. досить з надлишком для створення усіх білків.
досить з надлишком для створення усіх білків. де
де 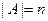 . Якщо порядок елементів неістотній, то множина називається невпорядкованою.
. Якщо порядок елементів неістотній, то множина називається невпорядкованою. , які утворюються за слідуючим правилом:
, які утворюються за слідуючим правилом: вибираємо будь-який елемент
вибираємо будь-який елемент 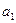 ; із множини А
; із множини А вибираємо
вибираємо 
 вибираємо
вибираємо 
 вибираємо
вибираємо 

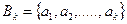 - це буде вибірка без повторень, вона впорядкована, якщо кожному вибраному елементу множини
- це буде вибірка без повторень, вона впорядкована, якщо кожному вибраному елементу множини  поставити у відповідність номер. Отримали впорядковану k вибірку без повторів. А якщо елементам множини
поставити у відповідність номер. Отримали впорядковану k вибірку без повторів. А якщо елементам множини  .
. . Загальна кількість різних розміщень позначається
. Загальна кількість різних розміщень позначається  .
.
 - згідно правила добутку. Даний вираз можна переписати у вигляді
- згідно правила добутку. Даний вираз можна переписати у вигляді де
де 
 ;
;  , зручному для користування.
, зручному для користування. .Ясно, що будь-які n -перестановки відрізняються лише порядком елементів, і кожна вибірка містить усі елементи множини А.
.Ясно, що будь-які n -перестановки відрізняються лише порядком елементів, і кожна вибірка містить усі елементи множини А. .У слові міссісіпі є 4-і, 3-с. Ясно, що якщо здійснити перестановки “і” то отримаємо 4! перестановок, що збігаються. Аналогічно для “с” їх 3!
.У слові міссісіпі є 4-і, 3-с. Ясно, що якщо здійснити перестановки “і” то отримаємо 4! перестановок, що збігаються. Аналогічно для “с” їх 3! при умові, що вони різні буде менше у
при умові, що вони різні буде менше у 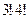 раз, а отже
раз, а отже 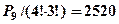 різних перестановок.
різних перестановок. - першого типу,
- першого типу,  - другого,
- другого,  - 3-го і т.д.
- 3-го і т.д.  - того так, щоб
- того так, щоб 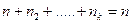 . Такі перестановки називають перестановками з повторенням так як елементи у вибірках повторюються. Переставляючи однакові елементи ми отримаємо
. Такі перестановки називають перестановками з повторенням так як елементи у вибірках повторюються. Переставляючи однакові елементи ми отримаємо  однакових перестановок. Якщо б усі елементи були різними то усіх можливих перестановок було б n! - повне число перестановок без повторів. Тоді, число різних перестановок з повторами можна обчислити за формулою
однакових перестановок. Якщо б усі елементи були різними то усіх можливих перестановок було б n! - повне число перестановок без повторів. Тоді, число різних перестановок з повторами можна обчислити за формулою , де
, де  .
. . Кожному елементу множини
. Кожному елементу множини  , що входить в сполуку, поставимо у відповідність 1, а елементам, що не входять поставимо “0”. Тоді будь-якій сполуці з “n” по “k” відповідає єдина “n” - перестановка з повторенням, що містить к -одиниць та n - к – нулів.
, що входить в сполуку, поставимо у відповідність 1, а елементам, що не входять поставимо “0”. Тоді будь-якій сполуці з “n” по “k” відповідає єдина “n” - перестановка з повторенням, що містить к -одиниць та n - к – нулів. . Ми отримали відомий вираз для обчислення кількості різних сполук.
. Ми отримали відомий вираз для обчислення кількості різних сполук.
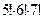 раз, а отже,
раз, а отже,  .
.

 - кількість, де двійка виникає із-за наявності (1,1) та (3,3),
- кількість, де двійка виникає із-за наявності (1,1) та (3,3),  - перестановки трьох вільних елементів, інших ніж вибрані. Іще є варіант кодового слова де співпадають два числа їх кількість буде
- перестановки трьох вільних елементів, інших ніж вибрані. Іще є варіант кодового слова де співпадають два числа їх кількість буде 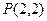 .
.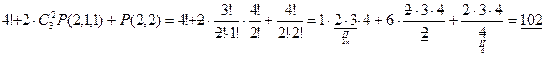 .
. 0
0  0 _ 0
0 _ 0  12-1
12-1 m 3-0 Таким чином, комбінацією елементів 111110111111001 описується даний розподіл. Усіх елементів отримано 12+4-1=15.
m 3-0 Таким чином, комбінацією елементів 111110111111001 описується даний розподіл. Усіх елементів отримано 12+4-1=15.  елементів з повторами, яка містить n -одиниць та m-1 – нулів. Це є код відповідного розміщення.
елементів з повторами, яка містить n -одиниць та m-1 – нулів. Це є код відповідного розміщення.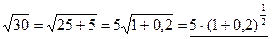 а дальше ряд Ньютона
а дальше ряд Ньютона дозволить обчислити значення з довільною, бажаною степеню точності.
дозволить обчислити значення з довільною, бажаною степеню точності.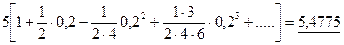 .
.
 500
500 в ряд по степенях b став називатись біномом Ньютона.
в ряд по степенях b став називатись біномом Ньютона.


