
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема замещения фазы обмотки статораСодержание книги Поиск на нашем сайте
Перечислим параметры, которые описывают основные процессы, происходящие в фазе обмотки статора. Активное сопротивление фазы статора намного меньше реактивного, поэтому мы его учитывать не будем. К фазе обмотки статора приложено напряжение
ротора наводит в ней ЭДС Схема замещения фазы обмотки статора, отражающая связь указанных параметров, показана на рис. 4.4. Направление стрелки тока выбрано так, чтобы это было удобно для исследования генераторного режима. Согласно схеме, уравнение фазы обмотки статора имеет вид:
Угловая характеристика Зависимость момента на валу от угла q называется угловой характеристикой машины. Можно показать, что она приближенно выражается формулой
где М – вращающий момент машины, kM = 28,6 k, – коэффициент, зависящий от конструкции машины,
Поэтому графики угловых характеристик генератора для фиксированных значений напряжения и тока статора и для различных значений тока возбуждения имеют вид, показанный на рис. 4.5. При работе СМ необходимо, чтобы момент на валу был меньше, чем максимально возможный момент для данного тока возбуждения. Если это условие не соблюдается, то случается авария – СМ "выпадает из синхронизма". При этом частота вращения ротора отличается от частоты вращения магнитного поля статора, момент на валу машины пульсирует, а его среднее значение становится близким к нулю. Это может привести к тяжелым последствиям. Чтобы избежать этой аварии, нужно задавать такой ток возбуждения, который обеспечивал бы некоторый запас момента. Модуль угла q должен быть заведомо меньше Дополнительные пояснения Уравнение угловой характеристики можно вывести так. Активная генерируемая мощность фазы машины равна Из уравнения фазы выразим ток
Но Учитывая, что
Здесь нужно учесть, что для генератора сам угол q принимает отрицательные значения (это фаза напряжения минус фаза ЭДС, см. рис. 4.6), поэтому генерируемая мощность получается положительной. Потребляемая механическая мощность на валу равна Пренебрегая потерями энергии в машине, приравняем механическую и электрическую мощности, получим: Учитывая, что Заметим, что отношение
Обозначив 28,6 k = kM, получим приведенную выше формулу. U - образная характеристика
В соответствии со схемой замещения фазы машины и с уравнением (4.3) нарисуем векторные диаграммы генератора. Пусть действующее значение напряжения сети, к которой подключен СГ, постоянно. Выберем начальную фазу напряжения равной нулю. Рассмотрим различные состояния генератора для одинаковых значений активной генерируемой мощности. Так как
Векторные диаграммы рис. 4.6 показывают, что при различных значениях ЭДС Е 0 получаются различные углы сдвига фаз j между напряжением и током СМ. ЭДС Е 0 пропорциональна току возбуждения (см. уравнение 4.2). Поэтому угол j и ток статора I зависят от тока возбуждения. Эту зависимость называют U-образной характеристикой и изображают в виде, показанном на рис. 4.7. Большим значениям мощности соответствуют большие значения тока возбуждения, необходимые для обеспечения устойчивости СМ, то есть для удержания угла q в пределах Возможность регулировки сдвига фаз между напряжением и током СМ является очень ценным качеством, позволяющим компенсировать реактивный ток нагрузки (см. п. 16) и сократить потери энергии в линиях электропередач. Иногда перевозбужденные СД используют только как компенсаторы реактивной мощности, без нагрузки на валу. СД имеют такие же угловые и U-образные характеристики, как и СГ. Различие состоит в знаке угла q. Вследствие этого перевозбуждению СД соответствует j < 0, а недовозбуждению j > 0. Следует также учесть, что генератор отдает, а двигатель потребляет электромагнитную мощность, поэтому все приведенные выше рассуждения будут справедливы и применительно к двигателю, если изменить знак мощности, направление стрелки тока на схеме (4.4) и знак перед слагаемым jx в уравнении (4.3).
|
||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.13.244 (0.008 с.) |

 . Магнитное поле
. Магнитное поле Рис. 4.4. Схема
замещения фазы
обмотки статора СМ.
Рис. 4.4. Схема
замещения фазы
обмотки статора СМ.
 . По фазе обмотки течет ток
. По фазе обмотки течет ток  . Фаза обладает активным сопротивлением r и реактивным сопротивлением jx, которое обусловлено магнитными потоками рассеивания статора.
. Фаза обладает активным сопротивлением r и реактивным сопротивлением jx, которое обусловлено магнитными потоками рассеивания статора. . (4.3)
. (4.3) , (4.4)
, (4.4) – ток фазы статора,
– ток фазы статора,  – ток возбуждения.
– ток возбуждения. Рис. 4.5. Угловые характеристики СГ.
Рис. 4.5. Угловые характеристики СГ.
 .
. , где черта наверху означает комплексное сопряжение.
, где черта наверху означает комплексное сопряжение. и подставим это выражение в формулу для мощности, получим:
и подставим это выражение в формулу для мощности, получим: .
. – действительное число, поэтому мнимая часть его равна нулю.
– действительное число, поэтому мнимая часть его равна нулю. (см. формулу для реактивной мощности двухполюсника), из приведенного выше выражения для Р получим:
(см. формулу для реактивной мощности двухполюсника), из приведенного выше выражения для Р получим: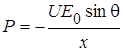 .
. , где М – вращающий момент машины (для генератора М < 0), w – угловая скорость ротора.
, где М – вращающий момент машины (для генератора М < 0), w – угловая скорость ротора. (здесь 3 – число фаз машины).
(здесь 3 – число фаз машины). , формулу для момента можно выразить через частоту вращения n:
, формулу для момента можно выразить через частоту вращения n:  . Подставив сюда
. Подставив сюда 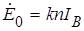 , получим:
, получим:  .
. равно току фазы статора
равно току фазы статора  .
.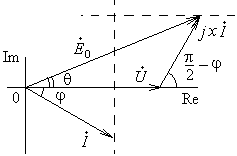 Перевозбуждение СГ. j > 0.
Перевозбуждение СГ. j > 0.
 j = 0
j = 0
 Недовозбуждение СГ. j < 0.
Рис. 4.6.
Недовозбуждение СГ. j < 0.
Рис. 4.6.
 ,
,  , то
, то  . Поэтому во всех случаях конец вектора
. Поэтому во всех случаях конец вектора  будет лежать на вертикальной пунктирной прямой (рис 4.6). Напряжение
будет лежать на вертикальной пунктирной прямой (рис 4.6). Напряжение  , обусловленное магнитными потоками рассеивания, будет опережать по фазе ток на угол
, обусловленное магнитными потоками рассеивания, будет опережать по фазе ток на угол  , а его конец будет лежать на горизонтальной пунктирной прямой.
, а его конец будет лежать на горизонтальной пунктирной прямой. Рис. 4.7. U-образные характеристики для
различных значений активной мощности СГ.
Рис. 4.7. U-образные характеристики для
различных значений активной мощности СГ.
 . Граница области устойчивости показана рис. 4.7 слева пунктиром.
. Граница области устойчивости показана рис. 4.7 слева пунктиром.


