Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Извлечение примесей воды осаждениемСодержание книги
Поиск на нашем сайте
Теоретические основы процесса осаждения Основная масса взвешенных частиц в воде удаляется отстаиванием. Различают монодисперсную (частицы одинаковой гидравлической крупности) и полидисперсную взвесь. Скорости движения воды в отстойниках малы (десятые доли мм/с), вода практически полностью теряет свою транспортирующую способность. Осаждение взвеси в таком потоке подчиняется законам осаждения в покоящемся объёме жидкости. В неподвижной жидкости на осаждающуюся частицу действует: 1. Выталкивающая сила
W – объём частицы, 2. Сила сопротивления при падении частицы в жидкость (закон Ньютона-Рэлея)
3. Сила гравитации
Для монодисперсных шарообразных частиц диаметром d скорость свободного осаждения
При Re<0,2 на частицу действует только F гравитации (ламинарный режим)
Скорость свободного падения такой частички описывается уравнением Стокса:
Для более крупных частиц Re>2
При осаждении сила сопротивления равна силе тяжести
Определив К для частиц любого размера можно определить гидродинамические характеристики падающей частицы, коэффициент сопротивления Скорость осаждения Для монодисперсной взвеси количество выпавшего осадка за время
А – площадь цилиндра, с – концентрация исходной взвеси
Относительное количество выпавшей взвеси
Строят график зависимости выпадения осадка
Эффект осаждения может быть рассчитан по концентрации взвеси в исходной и осветлённой воде.
Из графика находим
При осаждении устойчивой взвеси продолжительность пребывания воды в отстойнике во столько раз больше продолжительности осаждения в цилиндре во сколько раз высота зоны осаждения больше высоты слоя в цилиндре. Для неустойчивой коагулирующей взвеси при расчёте отстойников следует использовать уравнение
Седиментационный анализ при определении размеров взвешенных частиц в сточной воде выполняется с использованием торзионных весов, плотность осадка определяется весовым методом.
Рисунок 1 – Торзионные весы 1–металлическая опора; 2 – тренога; 3 – опорные винты; 4 – шкала для взвешивания; 5 – указатель веса; 6 – рычаг натяжения; 7 – указатель равонвесия; 8 – тарировочная головка; 9– коромысло; 10– крюк; 11– крышка; 12– закрепительный рычаг; 13– регулятор уровня. Весовой метод седиментационного анализа заключается в определении скорости накопления осадка на чашечке весов. По экспериментальным данным строится график зависимости относительной массы осадка от времени, так называемая накопительная кривая Радиус частиц определяется по формуле Стокса: dэк= где По экспериментальным данным строится график зависимости накопленной массы осадка от времени, так называемая накопительная кривая (рисунок 2), где Q – масса осадка накопившегося за время
Рисунок 2 – Накопительная кривая
Рисунок 3 –Дифференциальная кривая
Рисунок 4 –Интегральная кривая
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.153.50 (0.009 с.) |


 - плотность.
- плотность.

 - коэффициент сопротивления, является функцией Рейнольдса
- коэффициент сопротивления, является функцией Рейнольдса
 в неподвижной воде выражается уравнением:
в неподвижной воде выражается уравнением:
 -коэффициент сопротивления шарообразной частицы.
-коэффициент сопротивления шарообразной частицы.



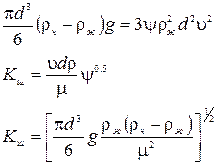

 частицы при 10
частицы при 10  называют гидравлической крупностью, которую находят экспериментально.
называют гидравлической крупностью, которую находят экспериментально.


 - массовое содержание взвеси в единице объема
- массовое содержание взвеси в единице объема
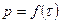 - кривая
- кривая Монодисперсная
Монодисперсная
 Полидисперсная
Полидисперсная
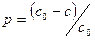 при
при 
 , затем
, затем  из соотношения подобия
из соотношения подобия , так как
, так как 



 , где Q-масса осадка накопившегося за время
, где Q-масса осадка накопившегося за время  Q/
Q/  – дифференциальная кривая, пик на этой кривой соответствует среднему радиусу частиц в суспензии.
– дифференциальная кривая, пик на этой кривой соответствует среднему радиусу частиц в суспензии. ,
, - вязкость жидкости, Па с;
- вязкость жидкости, Па с; 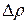 - разность плотностей дисперсионной и дисперсной фаз, кг/м3; g – ускорение свободного падения, м/с2; Wос – скорость осаждения, м/с.
- разность плотностей дисперсионной и дисперсной фаз, кг/м3; g – ускорение свободного падения, м/с2; Wос – скорость осаждения, м/с. , в % от общей массы осевших частиц. На основании накопительной кривой строятся дифференциальная и интегральная кривые (рисунок 3), пик на дифференциальной кривой соответствует среднему радиусу (r), а интегральная кривая (рисунок 4) показывает содержание частиц данного радиуса (r) в суспензии.
, в % от общей массы осевших частиц. На основании накопительной кривой строятся дифференциальная и интегральная кривые (рисунок 3), пик на дифференциальной кривой соответствует среднему радиусу (r), а интегральная кривая (рисунок 4) показывает содержание частиц данного радиуса (r) в суспензии.