
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое симметричная трёхфазная система напряжений прямого, обратного и нулевого порядка следования фаз?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любую симметричную систему трёх токов, напряжений, потоков одинаковой частоты (обозначим их А, В, С) можно однозначно представить в виде трёх систем: нулевой, прямой и обратной последовательности. Система прямой последовательности состоит из трёх векторов Система обратной последовательности состоит из трёх векторов Система нулевой последовательности образована тремя векторами, совпадающими по фазе: 17. как найти напряжения прямого, обратного и нулевого порядка следования фаз, если напряжения несимметричной трёхфазной системы равны Напряжение прямого порядка следования фаз Напряжение обратного порядка следования фаз Напряжение нулевого порядка следования фаз Порядок расчета трёхфазной цепи по методу симметричных составляющих. Чему равно фазное напряжение на неповреждённых фазах трёхфазного симметричного приёмника соединения звезда без нулевого провода, если фаза А оборвалась, а линейное напряжение генератора 380 В? Чему равно фазное напряжение на неповреждённых фазах симметричного приёмника соединения звезда без нулевого провода при к.з. в фазе А и линейном напряжении генератора 380 В? Переходные процессы Как формулируются законы коммутации? 1) в момент коммутации, ток через индуктивность имеет такое же значение, каким он был в момент, предшествующий коммутации. Записать общий вид решения для переходного тока в цепи первого порядка.
Как по виду изображённой схемы определить порядок дифференциального уравнения, описывающего переходной процесс в цепи? Что такое начальные условия при расчете переходных процессов? Начальные условия – это значения токов и напряжений в схеме при t=0. Также существуют докоммутационные
Какие начальные условия считаются независимыми и от «чего» они не зависят? Ток через индуктивность и напряжение на ёмкости являются независимыми начальными условиями. Независимыми в том смысле, что для данной задачи эти величины не зависят на какое напряжение включается данная катушка или ёмкость. По какой схеме следует искать ННУ? ННУ следует искать из докуммутационной схемы цепи, т.е. для режима цепи до коммутации Какие НУ считаются зависимыми? Значения остальных токов и напряжений (не через L и C) при По какой схеме ищутся ЗНУ и как это делается? ЗНУ ищутся по послекоммутационной схеме, определяемые по ННУ из законов Кирхгофа. Что такое постоянная времени цепи 1-го порядка? Постоянная времени – это время, в течение которого свободная составляющая тока по модулю уменьшается в е раз. За какое время переходный режим перейдет в установившийся? Если в схеме после коммутации все источники постоянны, то как будут зависеть от времени установившиеся токи и напряжения?
Источники в схеме после коммутации постоянны. Как поведут себя в установившемся режиме реактивные элементы цепи L и C? Источники в схеме после коммутации синусоидальны. Как учесть в установившемся режиме L и C? 14. записать вид решения для переходного тока в цепи с двумя реактивными элементами, если корни характеристического уравнения равны Порядок расчета переходного процесса в цепи 1-го порядка. Записать вид решения для переходного процесса в цепи с двумя индуктивностями. 16. записать вид решения для переходного процесса в цепи второго порядка, если корни характеристического уравнения
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.172.11 (0.007 с.) |

 , равных по величине и повёрнутых относительно друг друга на 120, причем вектор
, равных по величине и повёрнутых относительно друг друга на 120, причем вектор  отстаёт от вектора
отстаёт от вектора  на 120.
на 120.
 , равных по величине и повернутых относительно друг друга на 120, причем вектор
, равных по величине и повернутых относительно друг друга на 120, причем вектор  опережает вектор
опережает вектор  на 120.
на 120.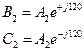
 .
.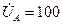
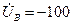
 ?
?



 - принуждённое значение тока, частное решение дифференциального уравнения, взятое в виде, какой имеет правая часть.
- принуждённое значение тока, частное решение дифференциального уравнения, взятое в виде, какой имеет правая часть. - свободное значение тока, решение однородного уравнения, соответствующее данному дифференциальному уравнению
- свободное значение тока, решение однородного уравнения, соответствующее данному дифференциальному уравнению непосредственно до коммутации и послекоммутационные
непосредственно до коммутации и послекоммутационные  после коммутации значения токов и напряжений.
после коммутации значения токов и напряжений. в послекоммутационной схеме, определяемые по ННУ из законов Кирхгофа называются зависимыми НУ.
в послекоммутационной схеме, определяемые по ННУ из законов Кирхгофа называются зависимыми НУ.
 ,
, 
 ,
,  .
.


