
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6 принципы квантовой механики. Уравнение Шредингера. Гипотеза де БройляСодержание книги
Поиск на нашем сайте
Основные формулы · Длина волны де Бройля при v<<c l = h / p · Для релятивистской частицы (v» c)
· Связь длина волны де Бройля с кинетической энергией частицы W k при v<<c
· Для релятивистской частицы
где W0 – энергия покоя. · Фазовая скорость волн де Бройля v = w/ k = W/p = c2/v · Групповая скорость волн де Бройля u = dw/dk = dW/dp = v. · Соотношение де Бройля W = hv = ћw; р = ћ k, где W –энергия частицы; р – импульс частицы; k – волновой вектор, n и w - частота и круговая частота волны де Бройля. · Стационарное уравнение Шредингера
где D - оператор Лапласа; y - волновая функция; m – масса частицы; W – полная энергия частицы; U - потенциальная энергия; ћ – постоянная Планка; · Плотность вероятности w обнаружить частицу в данной точке равна w = | y|2 · Вероятность обнаружить частицу в данном объеме V равна
· Вероятность обнаружить частицу в интервале от х1 до х 2
· Для частицы, находящейся на n энергетическом уровне в одномерной потенциальной яме, собственные значения энергии W n определяются по формуле
где l - ширина ямы. · Волновая функция для данного случая имеет вид
· Коэффициент преломления волн де Бройля на границе низкого потенциального барьера бесконечной ширины n = l1 ¤l2 = k 2 / k 1, где l1 и l2, k 1 и k 2 – длины волн де Бройля и волновые числа соответственно до барьера и на барьере соответственно. · Коэффициенты отражения r и пропускания d волн де Бройля через низкий барьер (U<W) бесконечной ширины
· Коэффициент прозрачность D прямоугольного потенциального барьера U шириной l определяется по формуле
Задачи 1. Найдите дебройлевскую длину волны молекул водорода, соответствующую их 2. Частица массы 10 г летит со скоростью 1000 м/с. Найдите длину волны де Бройля 3. Найдите длину волны де Бройля протона, прошедшего ускоряющую разность 4. Найдите длину волны де Бройля для протонов, прошедших ускоряющую 5. Найдите длину волны де Бройля электрона, прошедшего ускоряющую разность 6. Найдите дебройлевскую длину волны молекул водорода, соответствующую их 7. Найдите, при какой скорости электрона дебройлевская длина волны будет равна половине его комптоновской длины волны. Электрон считать релятивистским. 8. Найдите дебройлевскую длину волны атома урана, имеющего кинетическую 9. Найдите длину волны де Бройля нейтрона с энергией 0,023 эВ. 10.Найдите ускоряющую разность потенциалов, которую должен пройти электрон, чтобы длина волны де Бройля была равна 0,1 нм. Планка h = 6,63·10-34 Дж·с, заряд электрона е= - 1,6·10-19 Кл. 11.Найдите, на какую величину Dl будут отличаться значения дебройлевской длины волны частицы массы т, движущейся со скоростью v, если частицу считать:1- нерелятивистской, 2- релятивистской. 12.Найдите скорость частицы, при которой величины ее дебройлевской длины волны, вычисленные по нерелятивистской и релятивистской формулам, будут отличаться друг от друга на 10 %. 13.Найдите длину волны де Бройля для протона, имеющего кинетическую энергию Wk =1,67∙10-27кг/Дж∙с 14.Найдите длину волны де Бройля нерелятивистского электрона, имеющего кинетическую энергию 100 эВ, постоянная Планка h = 6,63·10-34 Дж·с., m 0 = 9,1·10-31 кг. 15.Электрон движется по окружности радиуса 5 см в однородном магнитном поле с индукцией 8 мТл. Найдите дебройлевскую длину волны электрона. Постоянная Планка h = 6,63·10-34 Дж·с. 16.Найдите длину волны де Бройля электрона, движущегося на второй боровской орбите атома водорода, постоянная Планка h = 6,63·10-34 Дж·с, mе = 9,1·10-31 кг. 17.Найдите, какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 пм до 50 пм, постоянная Планка h = 6,63·10-34 Дж·с, mе = 9,1·10-31 кг. 18.Найдите, при каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны. Комптоновская длина волны электрона λ = h/ (те∙ с). те = 9,1∙10- 31кг., 19.Найдите дебройлевскую длину волны протона с кинетической энергией, равной энергии покоя электрона. Протон считать нерелятивистским, h = 6,63·10-34 Дж·с, mе = 9,1·10-31 кг, mp =1,67∙10-27кг 20.Скорость частицы составляет 0,6 скорости света в вакууме. Найдите, на сколько процентов будут отличаться величины дебройлевской длины волны частицы, если вычисления производить по нерелятивистской и релятивистской формулам, 21.Найдите выражение для дебройлевской длины волны релятивистского протона, движущегося с кинетической энергией Wk 22.Интерпретируйте квантовые условия Бора на основе волновых представлений; покажите, что электрон в атоме водорода может двигаться только по тем круговым орбитам, на которых укладывается целое число волн де Бройля. 23. Электрон находится в потенциальной яме шириной l на третьем энергетическом уровне. В каких точках этой ямы плотность вероятности нахождения электрона будет максимальна. В каких точках плотность вероятности нахождения электрона на 3 и 4 энергетических уровнях будет одинакова. 24..Электрон находится в потенциальной яме шириной l на втором энергетическом уровне. В каких точках этой ямы плотность вероятности нахождения электрона будет максимальна. В каких точках плотность вероятности нахождения электрона на 2 и 3 энергетических уровнях будет одинакова 25. Электрон находится в потенциальной яме шириной l =0,1мкм на втором энергетическом уровне. Определить энергию и импульс электрона на этом уровне. Найдите вероятность нахождения электрона на промежутке l /2 –3 l /4. 26. Электрон находится в двумерной потенциальной яме со сторонами l 1 и l 2 на втором энергетическом уровне. Определить точки в этой яме, где вероятность нахождения электрона на этом уровне максимальна. 27.Электрон с энергией W =100 эВ попадает на потенциальный барьер высотой U = 64 эВ. Определить вероятность того, что электрон отразится от барьера.Прямоугольный барьер имеет ширину l = 0.1нм. При какой разности энергий U-W вероятность прохождения барьера электроном составит 50%. 28. Ядро испускает a - частицу с энергией 5 МэВ. Найти коэффициент прозрачности потенциального барьера высотой U=10 МэВ и шириной 5фм. 29. Протон и электрон прошли одинаковую ускоряющую разность потенциалов Dj=10кВ. Во сколько раз отличаются прозрачности для этих частиц, если высота барьера равна 20 кэВ и ширина 0,1нм.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |



 ,
, ,
, - здесь р – импульс частицы; k - волновое число.
- здесь р – импульс частицы; k - волновое число.

 ,
,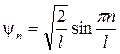
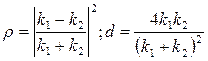 .
.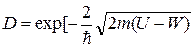 l ]
l ]


