
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Детерминирование системы без последствийСодержание книги
Поиск на нашем сайте
Они определены в том случае, если задана динамика развития системы с помощью оператора перехода, оператора выхода. Оператор переходов:
Если зафиксировать (t) – движение системы при зафиксированных значениях Множество всех движения системы обозначим совокупность упорядоченных пар (t,
Свойства оператора перехода: 1) Нулевое условие. 2)
Условие однозадачности. Оператор выходов:
Определение динамики выходных сигналов. В отличие от оператора переходов H, который каждый момент времени t на интервале от Совокупность точек Модель функционирования агрегата. ИС отличаются большим числом элементов, которые могут иметь разный характер и разнообразное взаимодействие между элементами. Поэтому для описания ИС вводится понятие агрегата. Это унифицированная модель для описания функционирования разнородных элементов систем. Динамика ИС может быть записана с помощью сопряженных между собой агрегативных моделей элементов Агрегат характеризуется множеством моментов времени T, состоянием в каждый момент времени Z, входным сигналом
Если за интервал времени
Во множестве состояний Z можно выделить некое подмножество
В некоторых случаях возможно изменение состояния системы в момент выдачи выходного сигнала, когда состояние
Таким образом, совокупность операторов Процесс функционирования агрегата состоит из скачковых состояний в момент поступления входного сигнала ( Для создания такой агрегатной модели функционирования ИС необходимо: 1.Разработать агрегатные модели элементов. 2.Построить модель сопряжения между элементами. Структуры систем управления (децентрализованная, централизованная, централизованная рассредоточенная, иерархическая). Агрегат может быть управляемым, а для того, чтобы рассмотреть управление агрегата, необходимо из множества входных сигналов выделить подмножество управляющих сигналов. С этом случае модель функционирования ИС зависит от принятых принципов управления. Рассмотрим основные классы структуры системы управления.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.148.57 (0.009 с.) |


 ,
,  и
и  , то получим состояние системы, как функцию времени t, где
, то получим состояние системы, как функцию времени t, где  .
. 

 ,
,  . Имеем при фиксированных
. Имеем при фиксированных 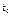 и z(
и z( )
) )
)  .
. (t) и совокупность этих пар называется разовой траектории системы, а совокупность точек пространства Z, которое соответствует всем t из множества T, называется траекторией системы в пространстве состояний. Эта траектория системы является пропорцией фазовых траекторий на пространство состояний.
(t) и совокупность этих пар называется разовой траектории системы, а совокупность точек пространства Z, которое соответствует всем t из множества T, называется траекторией системы в пространстве состояний. Эта траектория системы является пропорцией фазовых траекторий на пространство состояний.



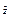 , оператор G на каждом моменте времени t определяет выходной сигнал. Оператор
, оператор G на каждом моменте времени t определяет выходной сигнал. Оператор  - оператор функционирования системы.
- оператор функционирования системы.

 , которое соответствует всем моментам времени
, которое соответствует всем моментам времени  , называется траекторией функционирования системы.
, называется траекторией функционирования системы. и выходным сигналом
и выходным сигналом  .Для агрегата рассматривается каждое состояние системы в момент времени t
.Для агрегата рассматривается каждое состояние системы в момент времени t  , так и в момент времени (t + 0)
, так и в момент времени (t + 0)  , в который агрегат может перейти за малый промежуток времени. Вид оператора перехода H будет зависеть от того, поступил или нет входной сигнал в течение рассмотренного промежутка времени. Пусть в момент времени
, в который агрегат может перейти за малый промежуток времени. Вид оператора перехода H будет зависеть от того, поступил или нет входной сигнал в течение рассмотренного промежутка времени. Пусть в момент времени  в агрегат поступает входной сигнал
в агрегат поступает входной сигнал  , тогда состояние агрегата в момент времени
, тогда состояние агрегата в момент времени  + 0:
+ 0: при
при  .
. в систему не поступило механических сигналов за исключением момента времени
в систему не поступило механических сигналов за исключением момента времени  , то:
, то: при
при 

 , что если составить
, что если составить  будет достигнуто состояние
будет достигнуто состояние  , то момент t* будет являться моментом выдачи агрегатом выходного сигнала:
, то момент t* будет являться моментом выдачи агрегатом выходного сигнала:
 выходит на границу
выходит на границу  . Чтобы учесть этот факт, вводится
. Чтобы учесть этот факт, вводится  , который все это учитывает:
, который все это учитывает:
 задает ранее описанные нами операторы переходов H, а совокупность операторов H и G полностью определяет модель функционирования агрегата.
задает ранее описанные нами операторы переходов H, а совокупность операторов H и G полностью определяет модель функционирования агрегата. ), и в момент выдачи выходного сигнала (
), и в момент выдачи выходного сигнала ( ), а также в момент изменения состояния агрегата между этими моментами (
), а также в момент изменения состояния агрегата между этими моментами ( ). Агрегативное описание системы и ее элементов достаточно универсально и подходит для различных математических моделей функционирования элементов и систем.
). Агрегативное описание системы и ее элементов достаточно универсально и подходит для различных математических моделей функционирования элементов и систем.


