
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические системы. Алгебраические операции.Содержание книги
Поиск на нашем сайте
Алгебраическая Для алгебраической системы объекты наделяются различными математическими структурами путем определения 1 или нескольких операций, для которых объект V становится алгеброй. Алгебра – либо общий предмет, либо алгебра относящаяся к теории алгебраических операций, либо некая математическая модель. В простом случае задается бинарная операция:
В этом случае подмножество W называется множество производящих элементов или алфавитом объекта. В этом случае элементы подмножества W называются символами, а элементы V – словами. Алфавит временных объектов и алфавит алгебраического объекта, если алфавиты конечны, являются 1ми и теми же множествами. Особый интерес представляют объекты, у которых элементы входных и выходных параметров определяются на 1 и тех же множествах. Пусть существует множество I, разделим его на Тогда, множество Х, определяется следующим образом:
Тогда система Многие понятия ТС можно определить исходя основному определению системы, но для получения существующих результатов необходимо введение дополнительных структур. Стахостические системы без последствий. Пусть
Если зафиксировать Если зафиксировать Если зафиксировать
Динамические системы. Данное описание удобно тем, что используется богатый математический аппарат. В данном случае все переменные называются переменными состояния, а пространство, где меняется переменная, называется пространством состояний.
Rn – n-мерное Эвклидово пространство x – переменная состояния и определенная на Rn U – переменная состояния и определенная на Rm
y – переменная состояния и определенная на Rr Условия существования единственного решения выполняется в том случае, если переменная управления U(t) принадлежит одному из следующих классов функций: постоянная, кусочно-постоянная, кусочно-непрерывная, кусочно-гладка функция. Частными случаями динамической системы являются: линейные системы x’=Ax+Bu y =Cx билинейные системы
линейно-аналитическая система: x’(t)=f(x(t))+U(t)g(x(t)) y(t)=Cx(t)
Минусом динамических систем является отсутствие информации о топологии и структуре системы/модели.
Динамические системы можно представлять нелинейными ДУ:
x – внутренняя переменная системы f – внешнее воздействие на систему – смотри нормальную форму Коши
21. Графы. Основные определения. Графом G называется совокупность двух множеств X(вершин) и U (дуг), между элементами которых определено отношение инцидентности (связности или соседства), причем каждый элемент u Дуга Uj исходя из xi и заходит в xj. Такая дуга становится инцидентной вершинам xi и xj. Если взять две вершины Если записано x≤y следовательно x=y или из вершины x в y существует путь. Дуги называются смежными, если они различны, но имеют 1 общую вершину. Вершины смежные, если они различны и существует дуга из одной вершины в другую. Некая вершина Вершина
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.137.193 (0.008 с.) |

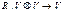 и предполагается, что в множестве V любой выделить такое подмножество W, что любой элемент из множества V можно получить в рез. применении операции R к элементам подмножества W.
и предполагается, что в множестве V любой выделить такое подмножество W, что любой элемент из множества V можно получить в рез. применении операции R к элементам подмножества W.
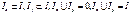
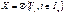 будем называть входящим объектом, а множество
будем называть входящим объектом, а множество 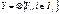 .
. носит название система вход/выход или система черного ящика.
носит название система вход/выход или система черного ящика.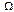 - пространство элементов случайных событий, и для каждого случайного события
- пространство элементов случайных событий, и для каждого случайного события 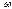 определена вероятность
определена вероятность 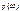 , тогда:
, тогда: =
=  - Оператор переходов.
- Оператор переходов.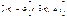 - Оператор выходов.
- Оператор выходов.
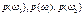
 , то система будет называться системой со случайными начальными состояниями.
, то система будет называться системой со случайными начальными состояниями. , то будет получена система со случайными переходами.
, то будет получена система со случайными переходами.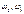 , то будет получена система со случайными выходами.
, то будет получена система со случайными выходами.
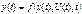
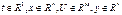
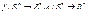
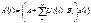 Y(t)=Cx(t)
Y(t)=Cx(t)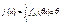 – это для перехода от векторной формы к матричным преобразованиям.
– это для перехода от векторной формы к матричным преобразованиям. 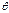 – матрица Якоби.
– матрица Якоби.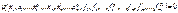 i=1,n
i=1,n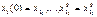
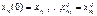
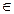 U, инцидентен ровно двум элементам x1,x2
U, инцидентен ровно двум элементам x1,x2 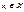 , и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x.
, и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x.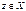 , которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.
, которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.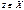 , которая предшествует всем вершинам подмножества Y множества X называется минорантой (истоком). Может существовать несколько минорант.
, которая предшествует всем вершинам подмножества Y множества X называется минорантой (истоком). Может существовать несколько минорант.


