
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотная и фазовая модуляция аналоговых сообщенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основные определения. Поскольку мгновенная частота ω (0 с фазой θ(t) сигнала связана соотношением
то частотная и фазовая модуляция взаимозависимы, их объединяют даже общим названием — угловая модуляция. При частотной модуляции (ЧМ) мгновенная частота сигнала изменяется по закону модулирующего сигнала, при фазовой (ФМ) — фаза- Поэтому при модуляции тестовым синусоидальным сигналом частотой Ω
uмод(t)= Uмод cosΩt (7.2)
При ЧМ и ФМ соответственно получим:
ω(t) = ω0 + ΔωдcosΩt, (7.3)
где Δωдев = kUмол — девиация частоты;
θ(t) = ω0t + ΔφдcosΩt + θ0 (7.4)
где Δφдев = kUмол — девиация фазы. Высокочастотное, несущее колебание
u(t) = U0.cosθ(t) (7.5)
При частотной модуляции тональным сигналом (8.2) с учетом (7.3) несущее колебание (7.5) примет вид (рисунок 7.1)
где mч = Δω/Ω — индекс частотной модуляции.
Рисунок 7.1 Вид частотной модуляции тональным сигналом При фазовой модуляции тональным сигналом (7.2) с учетом (7.4) несущее колебание (7.5) принимает вид
где Δφдев — девиация фазы, или индекс фазовой модуляции. Из (7.6) и (7.7) следует, что при частоте модулирующего сигнала Ω = const отличить частотную модуляцию от фазовой не представляется возможным. Это различие можно обнаружить только при изменении частоты Ω. При ЧМ согласно (7.6) девиация частоты Δωдев = const при изменении частоты Ω, а девиация фазы сигнала меняется по закону Δφдев = Δωдев/Ω При ФМ согласно (7.7) амплитуда колебания фазы сигнала Δφдев = const, а мгновенная частота сигнала меняется по закону
ω(t) = ω0 - Δφд Ωsin Ωt, (7.8) следовательно, девиация частоты пропорциональна частоте модулирующето сигнала Δωдев = Δφдев Ω. Данное различие между ЧМ и ФМ иллюстрируется с помощью графиков, построенных на рисунке 7.2. Таким образом, при обоих видах угловой модуляции (ЧМ и ФМ) меняется как мгновенная частота, так и фаза модулируемого ВЧ сигнала. Однако два основных параметра, характеризующих эти виды модуляции — девиация частоты Δωдев и девиация фазы Δφдев, — по-разному зависят от частоты модулирующего сигнала Ω.
Рисунок 7.2 Различие между ЧМ и ФМ
Спектр сигнала при частотной и фазовой модуляции. Обратимся к выражению для ЧМ сигнала (7.6), представив его в виде суммы двух слагаемых:
u(t) =
Разложив периодические функции в (7.9) в ряд Фурье, имеем
где Jn(mч) — бесселевая функция 1-го рода n-го порядка от аргумента m; п — целое число. Программа и графики бесселевой функции при n = 0...5 и mч = х = 0...20
I0(x):=J0(x) I1(x):=J1(х) I2(x):= Jn(2,x) I3(x):=Jn(3,x) I4(x):=Jn(4,x) I5(x):= Jn(5,x) I
Рисунок 7.3 Графики бесселевой функции
Пакет программ Mathcad представляет возможность путем обращения к функции J0, J1, Jn вычислить значения бесселевой функции 1-го рода n-го порядка при любом значении аргумента mч. Согласно (7.10) при ЧМ спектр высокочастотного сигнала при тональном модулирующем сигнале частотой Ω имеет бесконечное число спектральных составляющих, расположенных симметрично относительно частоты ω0 через интервалы, равные Ω. Частоты этих спектральных составляющих равны ω0 ± Ω, а амплитуды — С помощью приведенных графиков можно построить спектр ЧМ и ФМ сигнала при заданном значении mч = х или Δφяев = х. В качестве примера такие спектрограммы при mч = 5 и mч = 2,4 приведены на рисунке 7.4. Следует заметить, что спектральная составляющая с частотой ω0 и несущая с частотой ω0 суть разные понятия. Так, при mч = 2,4 спектральная составляющая с частотой ω0 равна 0, но это не означает отсутствие несущей в сигнале. Теоретически спектр ЧМ сигнала безграничен. Однако, как показывает анализ, большая часть энергии ЧМ сигнала сосредоточена в полосе
Δfсп=2(1+mч +
где F — высшая частота в спектре модулирующего сигнала.
Рисунок 7.4 Спектр ЧМ и ФМ сигнала
Именно на эту величину и следует рассчитывать полосы пропускания ВЧ трактов радиопередатчиков и радиоприемников. При mч << 1 ширина спектра ЧМ сигнала: Δfсп= 2F. Частотная модуляция с индексом mч < 1 является узкополосной, с индексом тч > 2—3 — широкополосной. Преимущества частотной модуляции в полной мере реализуются при тч> 1.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (7.1)
(7.1) (7.6)
(7.6)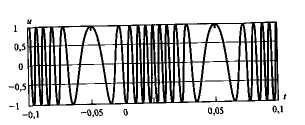
 (7.7)
(7.7)
 (7.9)
(7.9)
 (7.10)
(7.10)

 . Аналогичный результат получается и при фазовой модуляции с заменой параметра mч, на Δφяев.
. Аналогичный результат получается и при фазовой модуляции с заменой параметра mч, на Δφяев. (7.11)
(7.11)



