Собственное и вносимое затухания

 

При рассмотрении процессов, происходящих в последо­вательном и параллельном контурах, было показано, что добротность контура зависит от активного сопротивле­ния, входящего в контур. Добротность является крайне важ­ной характеристикой контура. В рассмотренных схемах кон­туров активное сопротивление входило в состав контура в виде конкретного резистора. Возникает вопрос, можно ли полностью избавиться от активного сопротивления, собрав контур только из индуктивности и емкости? Оказывается, сделать это невозможно.

Катушка индуктивности намотана проводом, который об­ладает определенным сопротивлением постоянному току, называемым омическим. Помимо этого, при прохождении переменного тока по проводу катушки ток вытесняется на поверхность провода. Это явление называется поверхностным эффектом. В качестве примера можно указать, что на частоте 1 МГц глубина проникновения тока в медном проводе оказы­вается менее 0,07 мм. Конечно же, это увеличивает сопротив­ление провода на высокой частоте.

Конденсаторы также нельзя считать приборами, обладаю­щими только емкостью. Диэлектрик, помещенный между пла­стинами конденсатора, имеет не бесконечно большое сопро­тивление. Поэтому контур имеет активное сопротивление,, которое на высокой частоте может значительно превышать омическое сопротивление провода катушки. Даже при отсутствии в его составе резисторов контур обладает конечной добротностью за счет наличия собственного активного со­противления.

Помимо собственного активного сопротивления контура в каком-либо устройстве почти всегда к нему параллельно присо­единены другие элементы схемы, в частности резисторы, которые оказываются подключенными параллельно актив­ному сопротивлению контура R₀, что приводит к уменьшению результирующего сопротивления, которым определяется добротность. Для оценки влияния внешних сопротивлений вводят понятие собственного и вносимого затуханий. Собствен­ное затухание контура определяется его собственным активным сопротивлением. Если это сопротивление включено в контур последовательно (например, активное сопротивление катушки индуктивности), собственное затухание находится по формуле:

 

. (2.14)

 

Если в контуре используется конденсатор с низким со­противлением изоляции R₀ , оно оказывается подключенным к контуру параллельно. Тогда собственное затухание контура за счет этого сопротивления находится по формуле:

 

(2.15)

 

Если контур содержит и активное сопротивление катуш­ки индуктивности г₀ и сопротивление изоляции конденсато­ра R₀, собственное затухание находится как сумма этих двух затуханий.

Когда к контуру в схеме подключено сопротивление како­го-то внешнего резистора R_ш, которое шунтирует контур, это приводит к появлению вносимого затухания:

 

(2.16)

 

При наличии двух или нескольких резисторов, подклю­ченных параллельно контуру, находят затухание, вносимое каждым из них, и затем их суммируют. Результирующее зату­хание контура находится сложением собственного и вноси­мого затуханий:

 

d = d₀ + d_вн. (2.17)

После определения полного затухания контура его доб­ротность находят, взяв обратную величину.

 

Полоса пропускания контура

На рисунке 2.7 были показаны резонансные кривые контуров при различных значениях их добротности. Чем больше доб­ротность контура, тем резонансная кривая оказывается уже.

Рисунок 2.8 К определению полосы пропускания

 

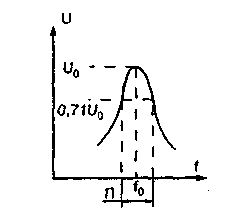
Для оценки ширины резонансной кривой используется поня­тие полосы пропускания контура, которой называется интер­вал частот вблизи резонансной частоты, на границах которо­го амплитуды тока или напряжения уменьшаются до 0,707 от их значения при резонансе. Это соответствует уменьшению мощности в два раза. На рисунке 2.8 показан способ определения полосы пропускания по резонансной кривой. Полоса про­пускания обозначается буквой П и измеряется в герцах, как и частота.

Можно доказать, что если известны резонансная частота контура и его добротность или затухание, полоса пропуска­ния находится путем умножения резонансной частоты на затухание:

 

П = f₀ d.

Знание полосы пропускания контура крайне важно, так как большинство устройств должно быть рассчитано на прохождение сигналов не одной определенной частоты, а цело­го спектра частот. Если полоса пропускания контура будет уже необходимой, крайние частоты этого спектра будут ослаблены. Если же полоса пропускания окажется шире необ­ходимой, устройство будет пропускать помехи, частоты ко­торых находятся вне полезного спектра. При необходимости можно воздействовать на полосу пропускания как в сторону ее сужения, так и в сторону расширения. Если необходимо сузить полосу пропускания, нужно увеличить добротность контура, например увеличением индуктивности и соответ­ствующим уменьшением емкости для сохранения прежней резонансной частоты. Если же необходимо расширить поло­су пропускания, это легко достигается подключением к кон­туру дополнительного шунтирующего резистора.

Шунтирование контуров резисторами в целях расшире­ния их полосы пропускания широко используется в радиоап­паратуре, например в телевизионных и радиолокационных приемниках.

 

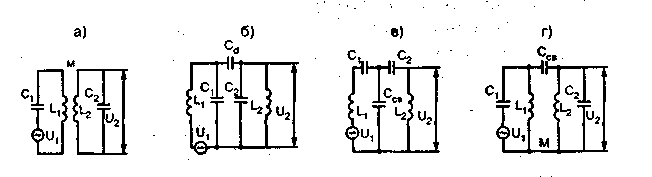
Связанные контуры

Колебательный контур является частотно-избирательной системой, пропуская сигналы, лежащие в его полосе пропус­кания, и ослабляя помехи, находящиеся вне полосы. Идеаль­ной для такого частотного фильтра была бы характеристика прямоугольной формы с плоской вершиной и крутыми склонами. Тогда сигналы проходили бы без ослабления, а помехи полностью подавлялись. Однако форма частотной характе­ристики одиночного контура весьма далека от идеальной. Значительно ближе к прямоугольным характеристики сис­тем из двух колебательных контуров. На рисунке 2.9 приведены схемы двухконтурных полосовых фильтров с разными спосо­бами связи между контурами. Коэффициент связи между ними k для схемы а равен отношению взаимной индуктивно­сти М к индуктивности контура, для схемы б - отношению емкости связи к емкости контура, для схемы в - отношению емкости контура к емкости связи. Для индуктивно-емкостной связи выражение для коэффициента связи сложнее, и при­водить его не будем.

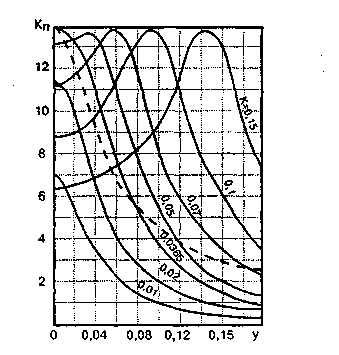
Рисунок 2.9 – Виды связи между контурами: индуктивная (а), внешне-емкостная (б), внутренне-емкостная (в) и индуктивно-емкостная (г)

Форма частотной характеристики зависит от соотноше­ния между коэффициентом связи и затуханием контуров. С увеличением коэффициента связи коэффициент передачи при резонансе растет, достигая максимума при k = d, а частот­ная характеристика одногорбая (один максимум). При дальнейшем увеличении коэффициента связи характеристика становится двугорбой (два максимума с провалом на часто­те резонанса), глубина провала растет, а горбы постоянно­го уровня раздвигаются.

На рисунке 2.10 показаны характеристики полосовых фильт­ров с индуктивностями по 300 мкГн, емкостями по 1000 пФ и активными сопротивлениями 20 Ом (затухание 0,0365) при разных коэффициентах связи. Пунктиром показана характе­ристика аналогичного одиночного контура, уменьшенная вдвое по высоте. Если сравнить ее с характеристикой двухконтурного фильтра при k = d, видно, что характеристика двухконтурной системы обладает более плоской вершиной и более крутыми склонами. Характеристики приведены для положительных значений относительной расстройки. В об­ласти отрицательных расстроек кривые располагаются симметрично.

В связи с тем, что при равенстве коэффициента связи за­туханию происходит переход от одногорбой характеристи­ки к двугорбой, такая связь называется критической.

При критической связи резонансный коэффициент пере­дачи максимален, и таков же коэффициент передачи при свя­зи больше критической.

 

Рисунок 2.10 АЧХ полосовых фильтров