
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Види модуляції, застосовувані в системах із чпкСодержание книги
Поиск на нашем сайте
У системах із ЧПК для піднесучих найбільше поширення одержали гармонічні коливання. Модульоване гармонічне коливання можна подати виразом:
де U(t) і Ф(t) – огинаюча і фаза модульованого коливання. У загальному випадку U(t) і Ф(t) не тільки функції часу, але й функції модулюючого коливання. У першому ступені системи з ЧПК таким коливанням буде передане канальне повідомлення 1) амплітудна 2) кутова 3) амплітудно-кутова (змішана) Кутова модуляція поділяється, у свою чергу, на фазову і частотну модуляції. У найпростішому випадку U(t) і Ф(t) зв’язані з 3.1.1. Лінійна амплітудна модуляція (АМ) та її властивості У цьому випадку амплітуда модульованого коливання U(t) визначається змінами модулюючого коливання:
де У більшості випадків модулююче коливання
де Отже, амплітуда модульованого гармонічного коливання:
де Врахувавши (3.2) і (3.3), позначимо Для одержання неспотвореної модуляції використовуємо тільки лінійну частину модуляційної характеристики, тобто
Для розрахунку спектра AM із використанням (3.1)–(3.3) модульоване коливання запишемо як суму гармонічних складових:
З виразу (3.4) випливає, що спектр AM при складному модулюючому коливанні Для більш ефективного використання потужності передавача в деяких системах зв’язку при передачі використовується тільки одна бічна спектра AM. Такий вид передачі називається однобічною чи односмуговою модуляцією (ОБМ). Односмуговій модуляції властиві деякі переваги, що мають особливо велике значення при передачі великих потоків інформації. Крім безпосереднього енергетичного виграшу на передавальній стороні системи, зумовленого тим, що вся потужність передавача використовується на створення однієї бічної, застосування ОБМ дає додатковий виграш, тому що дозволяє вдвічі звузити смугу пропускання приймача. Отже, по-перше, при лінійній AM спектр модульованого коливання для будь-якої форми модулюючого коливання завжди симетричний; по-друге, повна ширина спектра при AM дорівнює подвоєній найвищій (граничній) частоті спектра модулюючого коливання; по-третє, потужність кожної бічної смуги спектра AM залежить від величини 3.1.2. Лінійна фазова модуляція (ФМ) та її властивості У цьому випадку амплітуда модульованого коливання постійна, тобто
де З врахуванням раніше прийнятих позначень
Позначимо
Фаза модульованого коливання визначається:
Величина
Скориставшись результатами теорії функцій Бесселя, знайдемо спектр цього коливання, тобто зобразимо коливання
і врахуємо відоме з теорії функцій Бесселя співвідношення [2]
де Тоді
З огляду на те, що для цілих значень k справедливе співвідношення
Тоді вираз (3.7) можна записати у вигляді:
Вираз для спектра при ФМ гармонічним коливанням такий:
З (3.12) випливає, що спектр ФМ навіть при модуляції одним гармонійним коливанням має нескінченну кількість дискретних складових, утворюючих верхню і нижню бічні смуги спектра. Складові нижньої і верхньої бічних, симетричні відносно несучої, мають однакові амплітуди. Фази парних складових збігаються, а непарних – протилежні. Амплітуда несучої модульованого коливання визначається величиною Ширину спектра ФМ можна вважати скінченною величиною, що залежить від обраного значення
У загальному випадку визначити значення k з цієї умови не можна. Е.І.Манаєв [3] запропонував для визначення k наближений вираз:
Цей вираз дає добру точність для найбільш часто застосовуваних індексів модуляції у межах
Отже, ширину спектра ФМ визначаємо як
Це співвідношення називають формулою Манаєва. Іноді ширину спектра ФМ визначають, виходячи з менш жорстких умов. Якщо враховувати тільки ту частину спектра, гармоніки якої перевищують 5% амплітуди немодульованої несучої, то ширина спектра ФМ
Зауважимо, що неповне пропускання бічних смуг спектра ФМ (тобто обмеження спектра ФМ за частотою) приводить до появи помітної супутньої амплітудної модуляції і перекручуванню закону ФМ. Знайдемо середню питому потужність ФМ коливання. Відповідно до
З теорії функцій Бесселя відомо [2], що
Це означає, що при ФМ потужність випромінюваного коливання незмінна і дорівнює потужності несучої під час відсутності модуляції. Отже, при ФМ від передавача під час модуляції не потрібно додаткової потужності, і режим його роботи залишається незмінним. Якщо модуляція відсутня, то
Отримані результати залишаються справедливими для складного модулюючого коливання. У цьому випадку при визначенні ширини спектра ФМ у формулах (3.16) і (3.17) під частотою F потрібно розуміти верхню частоту спектра модулюючого коливання. Спектр ФМ навіть при модуляції одним гармонійним коливанням має нескінченну кількість дискретних складових, утворюючих верхню і нижню бічні смуги спектра. Складові нижньої і верхньої бічних, симетричні щодо несучої, мають однакові амплітуди. Фази парних складових збігаються, а непарних – протилежні. Отже, по-перше, спектр ФМ при будь-якому виді модулюючого коливання складається з нескінченної кількості складових; по-друге, ширина спектра ФМ, яка враховується на практиці, скінченна й залежить від значення індексу Лінійна частотна модуляція та її властивості Амплітуда модульованого коливання в цьому випадку постійна (так само, як і при ФМ), а частота коливання зв’язана лінійною залежністю з модулюючим коливанням, тобто
Тут З огляду на раніше прийняті позначення частота, модульованого коливання визначається
де Цей вираз визначає значення миттєвої частоти при модуляції коливанням складної форми. Неважко показати, що при використанні лінійної ділянки модуляційної характеристики
Запишемо вираз для коливання, модульованого за частотою. Врахуємо, що фаза і частота зв’язані співвідношенням:
де Як видно з виразу (3.22), коливання u(t) є функцією інтеграла від модулюючого коливання Провівши інтегрування вираження (3.21) і визначаючи повну фазу коливання, вираз ЧМ при складній формі модулюючої напруги можна записати у вигляді
де Порівнюючи вирази для коливання з ЧМ та ФМ, одержуємо, що вони відрізняються тільки початковими фазами. Тому всі результати, отримані для ФМ, справедливі й для ЧМ, з тією лише різницею, що у випадку ЧМ у всіх формулах під індексом модуляції Таким чином, лінійна ЧМ зводиться до лінійного ФМ, але з тією лише різницею, що індекс модуляції при ЧМ для кожної складової модулюючого коливання з частотою
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.63.136 (0.012 с.) |

 , (3.1)
, (3.1) , а в другому – багатоканальне повідомлення
, а в другому – багатоканальне повідомлення  . Позначимо модулююче коливання через
. Позначимо модулююче коливання через  . У залежності від того, в якому функціональному зв’язку знаходяться U(t) і Ф(t) з
. У залежності від того, в якому функціональному зв’язку знаходяться U(t) і Ф(t) з 
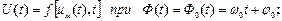



 – коефіцієнт, що характеризує чутливість модулятора, тобто показує, на яку величину змінюється амплітуда несучої при зміні модулюючої напруги на 1 В. Залежність U(t) від
– коефіцієнт, що характеризує чутливість модулятора, тобто показує, на яку величину змінюється амплітуда несучої при зміні модулюючої напруги на 1 В. Залежність U(t) від  ,(3.2)
,(3.2) – максимально можлива величина модулюючої напруги,
– максимально можлива величина модулюючої напруги,  – нормована модулююча функція, причому
– нормована модулююча функція, причому  .
. ,(3.3)
,(3.3) – коефіцієнт амплітудної модуляції.
– коефіцієнт амплітудної модуляції.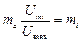 – парціальний коефіцієнт амплітудної модуляції, що відповідає i -му компоненту модулюючого коливання
– парціальний коефіцієнт амплітудної модуляції, що відповідає i -му компоненту модулюючого коливання  . Таким чином коефіцієнт модуляції при лінійній AM є складним коливанням, яке дорівнює сумі парціальних коефіцієнтів модуляції.
. Таким чином коефіцієнт модуляції при лінійній AM є складним коливанням, яке дорівнює сумі парціальних коефіцієнтів модуляції. . Отже, при модуляції миттєві значення моделюючої напруги не перевищують
. Отже, при модуляції миттєві значення моделюючої напруги не перевищують 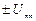 і виконується умова
і виконується умова  .
.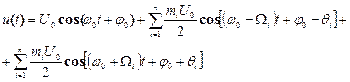 (3.4)
(3.4) й у випадку складного модулюючого коливання складає дуже малу частину потужності несучої. Оскільки спектральний компонент на частоті несучої не містить корисної інформації, а верхня і нижня бічні смуги спектра AM несуть однакову інформацію, то енергетично AM – дуже недосконалий вид модуляції.
й у випадку складного модулюючого коливання складає дуже малу частину потужності несучої. Оскільки спектральний компонент на частоті несучої не містить корисної інформації, а верхня і нижня бічні смуги спектра AM несуть однакову інформацію, то енергетично AM – дуже недосконалий вид модуляції. , а фаза зв’язана лінійною залежністю з модулюючою напругою:
, а фаза зв’язана лінійною залежністю з модулюючою напругою: , (3.5)
, (3.5) – коефіцієнт, що характеризує чутливість модулятора при ФМ, вказує на яку величину змінюється фаза при зміні модулюючої напруги, на 1 В. Для того щоб модуляція була лінійної, величина
– коефіцієнт, що характеризує чутливість модулятора при ФМ, вказує на яку величину змінюється фаза при зміні модулюючої напруги, на 1 В. Для того щоб модуляція була лінійної, величина  повинна бути постійною, тобто потрібно використовувати тільки лінійну ділянку модуляційної характеристики.
повинна бути постійною, тобто потрібно використовувати тільки лінійну ділянку модуляційної характеристики. .
. . Величина
. Величина  визначає максимальне відхилення фази коливання при модуляції і називається індексом фазової модуляції, що залежить тільки від амплітуди модулючого коливання та властивостей модулятора.
визначає максимальне відхилення фази коливання при модуляції і називається індексом фазової модуляції, що залежить тільки від амплітуди модулючого коливання та властивостей модулятора.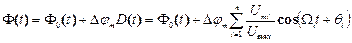 . (3.6)
. (3.6) – парціальний індекс фазової модуляції для складової з частотою
– парціальний індекс фазової модуляції для складової з частотою  . Отже, модульоване за фазою коливання можна подати у вигляді
. Отже, модульоване за фазою коливання можна подати у вигляді . (3.7)
. (3.7) у вигляді суми гармонічних складових. Для цього запишемо модульоване коливання у комплексній формі:
у вигляді суми гармонічних складових. Для цього запишемо модульоване коливання у комплексній формі: (3.8)
(3.8) , (3.9)
, (3.9) – функція Бесселя k -го порядку 1-го роду;
– функція Бесселя k -го порядку 1-го роду;  .
. . (3.10)
. (3.10) і беручи дійсну частину залежності (3.10), одержимо шуканий спектр. Вираз для спектра дуже громіздкий і незручний для користування. На практиці при розгляді ФМ вважають, що модуляція здійснюється гармонічним коливанням. При цій умові можна порівняно просто знайти всі співвідношення, а потім поширити їх на випадок складного модулюючого коливання. Нехай
і беручи дійсну частину залежності (3.10), одержимо шуканий спектр. Вираз для спектра дуже громіздкий і незручний для користування. На практиці при розгляді ФМ вважають, що модуляція здійснюється гармонічним коливанням. При цій умові можна порівняно просто знайти всі співвідношення, а потім поширити їх на випадок складного модулюючого коливання. Нехай .
. .(3.11)
.(3.11)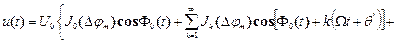
 (3.12)
(3.12) , що є функцією індексу фазової модуляції
, що є функцією індексу фазової модуляції  , що залежить від значення
, що залежить від значення  і враховують тільки ті складові, амплітуда яких перевищує задану величину. Звичайно приймають
і враховують тільки ті складові, амплітуда яких перевищує задану величину. Звичайно приймають  , де
, де  - частота модулюючого коливання; k - номер останньої врахованої складової, спричинений умовою
- частота модулюючого коливання; k - номер останньої врахованої складової, спричинений умовою (3.13)
(3.13)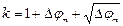 . (3.14)
. (3.14) . (3.15)
. (3.15) . (3.16)
. (3.16) . (3.17)
. (3.17) , проінтегрувавши вираз (3.12), одержуємо
, проінтегрувавши вираз (3.12), одержуємо . (3.18)
. (3.18) , тому
, тому . (3.19)
. (3.19) ,
,  і
і  , тобто вся потужність зосереджена на несучій частоті. При модуляції з’являються бічні складові спектра, потужність яких створюється за рахунок зменшення потужності компоненти на несучій частоті, тобто модуляція приводить до перерозподілу потужності коливання між його складовими таким чином, що загальна потужність коливання залишається незмінною. Розподіл потужності між окремими складовими спектра залежить від величини
, тобто вся потужність зосереджена на несучій частоті. При модуляції з’являються бічні складові спектра, потужність яких створюється за рахунок зменшення потужності компоненти на несучій частоті, тобто модуляція приводить до перерозподілу потужності коливання між його складовими таким чином, що загальна потужність коливання залишається незмінною. Розподіл потужності між окремими складовими спектра залежить від величини  рівна нулю, тобто для таких значень
рівна нулю, тобто для таких значень  . (3.20)
. (3.20) – коефіцієнт, що характеризує властивості модулятора при ЧМ. Він показує, на яку величину зміниться частота при зміні модулюючої напруги на 1 В.
– коефіцієнт, що характеризує властивості модулятора при ЧМ. Він показує, на яку величину зміниться частота при зміні модулюючої напруги на 1 В.
 , (3.21)
, (3.21) – максимальне відхилення частоти при модуляції і називається девіацією частоти,
– максимальне відхилення частоти при модуляції і називається девіацією частоти,  – парціальна девіація частоти за рахунок модулюючої складової коливання з частотою
– парціальна девіація частоти за рахунок модулюючої складової коливання з частотою  , тобто максимальна девіація частоти дорівнює сумі парціальних девіацій частот усіх складових модулюючого коливання.
, тобто максимальна девіація частоти дорівнює сумі парціальних девіацій частот усіх складових модулюючого коливання.
 , (3.22)
, (3.22) .
. , (3.23)
, (3.23) ,
,  ,
,  ,
,  – парціальний індекс частотної модуляції для складової з частотою
– парціальний індекс частотної модуляції для складової з частотою  .
. обернено пропорційній цій частоті, в той час як при ФМ індекс модуляції постійний і від частоти модуляції не залежить. Ця обставина приводить до відмінностей спектрів ЧМ і ФМ.
обернено пропорційній цій частоті, в той час як при ФМ індекс модуляції постійний і від частоти модуляції не залежить. Ця обставина приводить до відмінностей спектрів ЧМ і ФМ.


