
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Улучшение энергетики модулированных сигналов в системах с ЧРКСодержание книги
Поиск на нашем сайте
Из рассмотрения, приведенного в § 4.2, можно сделать вывод, что для получения неискаженной модуляции любого вида необходимо использовать только линейную часть соответствующей модуляционной характеристики. Превышение модулирующим колебанием некоторого определенного уровня (перемодуляция) приводит к появлению искажений. Этот уровень обычно называют уровнем полной линейной модуляции. Выбор его до некоторой степени условен и определяется величиной допустимых искажений, при которых используемый участок модуляционной характеристики можно еще рассматривать как линейный. Работа в пределах линейного участка модуляционной характеристики означает, что максимальное мгновенное значение модулирующего колебания не превышает уровня полной модуляции, т. е.
где Если модулирующее колебание
Параметры модуляции принимают максимальные значения только в тех случаях, когда фазы всех компонент, входящих в состав сложного модулирующего колебания, совпадут, т. е. когда Если при сложной форме модулирующего колебания параметры модуляции выбираются из приведенных условий, то окажется, что большую часть времени модуляционная характеристика используется не полностью. Это приведет к невыгодным энергетическим соотношениям, потому что средняя мощность боковых будет составлять малую часть общей мощности модулируемого колебания. Таким образом, стремление избежать перемодуляцию при сложной форме модулирующего колебания неизбежно приводит к ухудшению энергетических соотношений в спектре, модулированного колебания. Поэтому в некоторых случаях целесообразно перед модуляцией произвести ограничение больших выбросов мгновенных значений сообщения. Если до ограничения динамический диапазон сообщения определялся величиной
Рис. 4.10 Необходимо заметить, что ограничение динамического диапазона приводит к искажению передаваемых сообщений. Однако и в этом случае при разумно выбранных параметрах и с учетом увеличения помехоустойчивости общую ошибку при передаче сообщений можно уменьшить. Иногда применяют несколько иной способ уменьшения динамического диапазона передаваемого сообщения, называемый сжатием, или компрессией. Суть этого способа состоит в том, что сообщение предварительно пропускают через устройство с амплитудной характеристикой, изменяющейся по логарифмическому закону. Такое устройство называют компрессором сообщений. В результате сжатия динамический диапазон сообщения на выходе компрессора становится меньше, чем на его входе. Уменьшение динамического диапазона передаваемого сообщения компрессией имеет преимущество перед способом ограничения, так как в приемном устройстве можно восстановить первоначальную форму сообщения, пропустив его через схему с характеристикой, обратной характеристике компрессора. Эту схему обычно называют экспандером (расширителем). Однако абсолютно точного восстановления первоначального динамического диапазона практически получить нельзя, и сжатие при передаче будет вносить некоторую ошибку, которую можно сделать существенно меньше по сравнению с простым ограничением. Естественно, что преимущества способа сжатия перед способом ограничения достигаются за счет усложнения схемы. Параметры схем для уменьшения динамического диапазона передаваемого сообщения выбираются с учетом статистики сообщения. Если она неизвестна, то параметры определяют экспериментально, исходя при этом из величины ошибки, которую можно допустить. Вопрос о том, необходимо уменьшать динамический, диапазон сообщения или нет, решают с учетом конкретных условий, а также требуемого при этом усложнения аппаратуры. В настоящее время сжатие динамического диапазона сообщений применяется иногда в системах связи при передаче речи [8]. В радиотелеметрии такой способ из-за его сложности применяют реже, а при необходимости уменьшения динамического диапазона пользуются ограничением.
Рассмотрим вопрос о выборе параметров во второй ступени модуляции. Для того чтобы перемодуляция во второй ступени отсутствовала, сумма модулированных поднесущих никогда не должна превышать уровня, необходимого для обеспечения полной модуляции сигнала в радиолинии, т. е.
Здесь Skmi — максимальное значение амплитуды модулированного колебания i-той поднесущей; N—число каналов; Uлm — максимальный уровень, при котором перемодуляция во второй ступени еще отсутствует. Если амплитуды немодулированных поднесущих одинаковы и равны S0k, то в случае полной AM во всех каналах (т. е. во всех каналах mk=1) величина
Если поднесущие модулируются по частоте, то их амплитуда при модуляции не изменяется, поэтому для случая полной ЧМ во всех каналах
При допущении перемодуляции амплитуды поднесущих можно брать значительно больше тех значений, которые получаются из соотношений (4.88) и (4.89). Вероятность того, что сумма мгновенных значений N модулированных поднесущих в этом случае превысит уровень полной модуляции, может быть рассчитана. При расчете будем полагать, что фазы всех поднесущих случайны и равновероятны в интервале 0-2p. Обычно на практике это бывает в случае, когда применяются раздельные генераторы поднесущих в каждом канале (в частности, в радиотелеметрии). Для расчета указанной вероятности нужно знать функцию плотности вероятности W(x) колебания х, которое состоит из суммы N составляющих со случайными фазами, распределенными по равновероятному закону в интервале от 0 до 2p. Выражение для W(x) при небольших значениях N имеет довольно сложный вид, и здесь его не будем приводить. Однако при N³10 хорошим приближением для W(x) будет нормальный закон распределения [9], т. е.
где х—мгновенное значение суммы поднесущих, равное
В нашем случае
Если поднесущие модулируются по амплитуде с глубиной модуляции mk=l, то
Если все поднесущие имеют одинаковые амплитуды и модулируются по частоте, то
Напомним основные свойства функции W(x). Площадь, заключенная между кривой W(x) и осью абсцисс, (ось х), равна единице независимо от закона распределения плотности вероятностей:
В случае нормального закона функция W(x) четная относительно оси ординат, т. е.
Располагая функцией W(x), найдем вероятность того, что мгновенное значение суммы поднесущих х превысит уровень полной модуляции, т. е. найдем вероятность перемодуляции. Эта вероятность равна площади, заштрихованной на рис. 4.11, и определяется выражением
Рис. 4.11 Учитывая свойства функции W(x), имеем
или
Таким образом, чтобы определить вероятность перемодуляции, нужно знать вероятность, равную
т. е. вероятность того, что мгновенная сумма поднесущих не превысит допустимого уровня, т. е. вероятность отсутствия перемодуляции
или, с учетом выражения (4.90),
Делая замену переменных
получаем
Как известно,
называется интегралом вероятностей, или функцией Лапласа. Этот интеграл не может быть выражен через элементарные функции в конечном виде, поэтому значения Ф(a) табулированы для разных значений аргумента a. В частности, таблицы для Ф(a) содержатся в работе [10]. В некоторых таблицах и справочниках приводятся значения функции Крампа:
(4.107) или значения функции
Между всеми этими функциями имеется связь:
и при необходимости всегда можно выразить одну из этих функций через любую другую. Отметим, что Ф(a) —функция нечетная, т. е.
Итак, для данного случая имеем:
Проанализируем полученную формулу. Вероятность Найдем выражение для Н в случае амплитудной и частотной модуляций поднесущих. Наибольшие значения амплитуд AM и ЧМ поднесущих, при которых перемодуляция еще отсутствует, определяются выражениями (4.88) и (4.89). Если допустить перемодуляцию, то амплитуды поднесущих можно увеличить. Обозначим их через
и для ЧМ поднесущих
Используя эти соотношения, а также выражения (4.88), (4.89) и (4.103), получаем выражения для порогов перемодуляции при AM и ЧМ в виде:
откуда
Располагая полученными зависимостями, можно рассчитать допустимое увеличение амплитуды поднесущих при заданной вероятности перемодуляции. Расчет целесообразно вести в следующем порядке: 1) исходя из тактико-технических требований, задаемся величиной допустимой вероятности перемодуляции; 2) по заданной величине вероятности перемодуляции (табл. 4.1) находим величину порога перемодуляции; Таблица 4.1
3) зная величину порога Н и число каналов N, по формулам (4.114) и (4.115) находим, во сколько раз можно увеличить амплитуды поднесущих, вводя перемодуляцию. Рассмотрим пример. Пусть в системе с N=10 требуется найти увеличение поднесущих из-за введения перемодуляции во второй ступени с допустимой вероятностью p=10-3. Это значение вероятности говорит о том, что время, в течение которого происходит перемодуляция, составляет одну тысячную часть всего времени работы системы. Например, если время работы радиотелеметрической системы равно 5 мин, то общее время перемодуляции в среднем составит около 0,3 сек.
В этом примере величине p=10-3 соответствует Н=3,3. 3ная Н и N, по формулам (4.114) и (4.115) находим
Таким образом, при разумном допущении перемодуляции амплитуды подиесущих можно заметно увеличить, что приведет к более эффективному использованию модуляционной характеристики передающей части системы связи, и в результате улучшится энергетика модулированного сигнала. В заключение сделаем одно важное замечание. Нежелательно допускать перемодуляцию непосредственно в передатчике, потому что может произойти существенное паразитное расширение спектра сигнала. Кроме того, перегрузка модулятора приводит к появлению в нем сеточных токов, которые могут заметно изменить его входное и выходное сопротивления, в результате чего ухудшается работа передающей части системы. Поэтому практически после увеличения амплитуд поднесущих в соответствии с проведенным выше анализом полученное многоканальное сообщение перед подачей на вход модулятора нужно ограничить на уровне, определяемом величиной
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.133 (0.012 с.) |

 (4.85)
(4.85)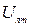 — уровень полной линейной модуляции.
— уровень полной линейной модуляции. имеет сложную форму, то максимальные значения параметров модуляции определяются как
имеет сложную форму, то максимальные значения параметров модуляции определяются как (4.86)
(4.86) . Однако вероятность такого события весьма мала и определяется статистическими свойствами модулирующего колебания. Мы говорим о модулирующем колебании как статистическом (т. е. случайном) процессе потому, что его точное аналитическое выражение никогда не известно. Могут быть известны только некоторые его характеристики, например верхняя граничная частота спектра, максимальное мгновенное значение, среднее значение и т. п.
. Однако вероятность такого события весьма мала и определяется статистическими свойствами модулирующего колебания. Мы говорим о модулирующем колебании как статистическом (т. е. случайном) процессе потому, что его точное аналитическое выражение никогда не известно. Могут быть известны только некоторые его характеристики, например верхняя граничная частота спектра, максимальное мгновенное значение, среднее значение и т. п. , то после ограничения — величиной
, то после ограничения — величиной  , т. е. уменьшится (рис. 4.10). При этом мощность боковых полос модулированного колебания возрастет, что в конечном счете увеличит помехоустойчивость канала связи.
, т. е. уменьшится (рис. 4.10). При этом мощность боковых полос модулированного колебания возрастет, что в конечном счете увеличит помехоустойчивость канала связи.
 (4.87)
(4.87)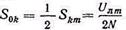 (4.88)
(4.88)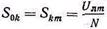 (4.89)
(4.89) (4.90)
(4.90)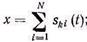 (4.91)
(4.91)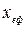 - эффективное значение суммарного колебания. По определению, эффективное (действующее или среднеквадратичное) значение любого колебания u(t)
- эффективное значение суммарного колебания. По определению, эффективное (действующее или среднеквадратичное) значение любого колебания u(t) (4.92)
(4.92) (4.93)
(4.93) (4.94)
(4.94)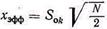 (4.95)
(4.95) (4.96)
(4.96) (4.97)
(4.97) (4.98)
(4.98)
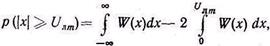 (4.99)
(4.99) (4.100)
(4.100)
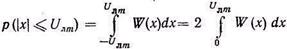 (4.101)
(4.101) (4.102)
(4.102)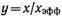 и обозначая
и обозначая (4.103)
(4.103) (4.104)
(4.104) (4.105)
(4.105) (4.106)
(4.106)
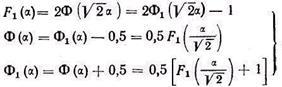 (4.108)
(4.108) (4.109)
(4.109) (4.110)
(4.110) (4.111)
(4.111) характеризует ту часть общего времени работы системы, в течение которой происходит превышение уровня полной модуляции, т. е. имеется перемодуляция. Эта часть времени зависит от величины Н, называемой порогом перемодуляции. Чем больше величина Н, тем больше порог и тем меньшее время происходит перемодуляция.
характеризует ту часть общего времени работы системы, в течение которой происходит превышение уровня полной модуляции, т. е. имеется перемодуляция. Эта часть времени зависит от величины Н, называемой порогом перемодуляции. Чем больше величина Н, тем больше порог и тем меньшее время происходит перемодуляция. тогда эффективное значение суммарного колебания для AM поднесущих
тогда эффективное значение суммарного колебания для AM поднесущих (4.94а)
(4.94а) (4.95а)
(4.95а) (4.112)
(4.112) (4.113)
(4.113) (4.114)
(4.114) (4.115)
(4.115)
 .
.


