Синтезувати в базисі Буля функціональні схеми пристроїв, які виконують дані операції, і навести значення сигналів на входах схеми і на виходах кожного елемента схеми.

 

a = (1ц1л)(2ц1л)(1ц2л)(2ц2л) = 3578₁₆ = 0011 0101 0111 1000₂

b = (1ц7л)(2ц7л)(1ц8л)(2ц8л) = 5328₁₆ = 0101 0011 0010 1000₂

 

 

Аргументи	a & b	a v b	a # b
a	b	(and)	(or)	(xor)

 

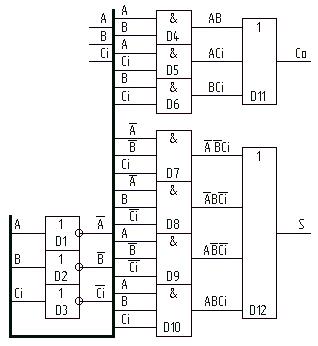
Схеми операцій в базисі Буля:

 

 

 

Аргументи	a & b	a v b	a # b
a	b	(and)	(or)	(xor)

 

 

4.2 Виконати операцію віднімання чисел у двійковому коді:

(1ц3л)(1ц1л)(2ц1л)-(1ц8л)(2ц8л),

(1ц8л)(2ц8л)-(1ц3л)(1ц1л)(2ц1л).

Від'ємний результат подати у прямому коді. Після виконання вказаних операцій навести у шістнадцятковому коді значення операндів і результату. Синтезувати на базі повних однорозрядних суматорів функціональну схему багаторозрядного суматора, який виконує дані операції, і навести значення сигналів на входах схеми і на виходах кожного однорозрядного суматора. Синтезувати в базисі Буля функціональну схему повного однорозрядного суматора, навести його таблицю істинності і значення сигналів на входах суматора і на виходах кожного його елемента для кожного розряду згаданого вище багаторозрядного суматора.

 

(1ц3л)(1ц1л)(2ц1л) = 335₁₆ = 0011 0011 0101₂

(1ц8л)(2ц8л) = 28₁₆ = 0010 1000₂

 

 

Виконання операції + 335 - 28

1) +335 + (-28);

2) 0.0011 0011 0101 + 1.0000 0010 1000 - числа у прямому двійковому коді, крапка відділяє в даному випадку знак числа від значущих розрядів числа;

3) 0.0011 0011 0101 + 1.1111 1101 1000 - числа у доповняльному двійковому коді;

4) 0.0011 0011 0101

+

1.1111 1101 1000

0.0011 0000 1101 - результат додатній у двійковому коді.

 

0.30D - результат у прямому шістнадцятковому коді.

Відповідь: +30D.

 

335 - 28 = 30D

Виконання операції +28 - 335

1) +28 + (-335);

2) 0.0000 0010 1000 + 1.0011 0011 0101 - числа у прямому двійковому коді, крапка відділяє в даному випадку знак числа від значущих розрядів числа;

3) 0.0000 0010 1000 + 1.1100 1100 1011 - числа у доповняльному двійковому коді;

4) 0.0000 0010 1000

+

1.1100 1100 1011

1.1100 1111 0011 - результат від'ємний у двійковому доповняльному коді.

5) 1.0011 0000 1101 - результат від'ємний у прямому двійковому коді.

 

1.30D - результат у прямому шістнадцятковому коді.

Відповідь: -30D.

 

28 - 335 = -30D

Таблиця істинності повного однорозрядного суматора:

Входи	Виходи
A	B	Ci	Co	S

 

З таблиці істинності видно, що

Co = /ABCi v A/BCi v AB/Ci v ABCi = BCi v ACi v AB;

S = /A/BCi v /AB/Ci v A/B/Ci v ABCi.

 

 

Функціональна схема повного однорозрядного сумматора:

 

Операція «335 - 28»:

A

B

Ci

D1

D2

D3

D4

D5

D6

D7

D8

D9

D10

D11

D12

/A

/B

/Ci

AB

ACi

BCi

/A/BCi

/AB/Ci

A/B/Ci

ABCi

Co

S

 

Операція «28 - 335»:

A

B

Ci

D1

D2

D3

D4

D5

D6

D7

D8

D9

D10

D11

D12

/A

/B

/Ci

AB

ACi

BCi

/A/BCi

/AB/Ci

A/B/Ci

ABCi

Co

S

 

 

Виконати округлення 16-розрядних двійкових кодів із точністю до 1/2 одиниці

молодшого розряду, який залишається. Коди:

Ц4л)(2ц4л)(1ц5л)(2ц5л) - від'ємне число в доповняльному коді,

Ц4л)(2ц4л)(1ц5л)(2ц5л) - додатне число в доповняльному коді.

При першому округленні відкинути два молодших розряди. Наступні округлення провести послідовно через кожних два двійкових розряди. Результат чергового округлення – це початкові дані для наступного округлення.

 

 

1(1ц4л)(2ц4л)(1ц5л)(2ц5л) = 1 (1723₁₆) = 1 1000 0111 0010 0011₂

0(1ц4л)(2ц4л)(1ц5л)(2ц5л) = 0 (1723₁₆) = 0 1000 0111 0010 0011₂

 

Округлення числа 1 1000 0111 0010 0011:

 

110 00 01 11 00 10 00(00)

+ 000 00 00 00 00 00 00(01)

110 00 01 11 00 11 00(01)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00 01 11 00 10 00(00)

 

 

110 00 01 11 00 10(00 00)

+ 000 00 00 00 00 00(01 11)

110 00 01 11 00 10(01 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00 01 11 00 10(00 00)

 

 

110 00 01 11 00(10 00 00)

+ 000 00 00 00 00(01 11 11)

110 00 01 11 00(11 11 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00 01 11 00(10 00 00)

 

 

110 00 01 11(00 00 00 00)

+ 000 00 00 00(01 11 11 11)

110 00 01 11(10 11 11 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00 01 11(00 00 00 00)

 

 

110 00 01(10 00 00 00 00)

+ 000 00 00(01 11 11 11 11)

110 00 01(11 11 11 11 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00 01(10 00 00 00 00)

110 00(01 00 00 00 00 00)

+ 000 00(01 11 11 11 11 11)

110 00(10 11 11 11 11 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110 00(01 00 00 00 00 00)

 

 

110(00 00 00 00 00 00 00)

+ 000(01 11 11 11 11 11 11)

110(11 11 11 11 11 11 11)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 110(00 00 00 00 00 00 00)

 

Округлення числа 0 1000 0111 0010 0011:

 

010 00 01 11 00 10 00(00)

+ 000 00 00 00 00 00 00(10)

010 00 01 11 00 10 00(10)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00 01 11 00 10 00(00)

 

 

010 00 01 11 00 10(00 00)

+ 000 00 00 00 00 00(10 00)

010 00 01 11 00 10(10 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00 01 11 00 10(00 00)

 

 

010 00 01 11 00(10 00 00)

+ 000 00 00 00 00(10 00 00)

010 00 01 11 01(00 00 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00 01 11 00(10 00 00)

 

 

010 00 01 10(00 00 00 00)

+ 000 00 00 00(10 00 00 00)

010 00 01 10(10 00 00 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00 01 10(00 00 00 00)

 

 

010 00 01(10 00 00 00 00)

+ 000 00 00(10 00 00 00 00)

010 00 10(00 00 00 00 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00 01(10 00 00 00 00)

010 00(01 00 00 00 00 00)

+ 000 00(10 00 00 00 00 00)

010 00(11 00 00 00 00 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 00(01 00 00 00 00 00)

 

 

010 (00 00 00 00 00 00 00)

+ 000 (10 00 00 00 00 00 00)

010 (10 00 00 00 00 00 00)

Розряди, які відкидаються, взято в дужки.

Результат першого округлення: 010 (00 00 00 00 00 00 00)

 

4.4 Виконати операцію віднімання чисел у двійково-десятковому коді (числа задані в шістнадцятковому коді):

(1ц1л)(2ц1л)-(1ц8л)(2ц8л),

(1ц8л)(2ц8л)-(1ц1л)(2ц1л).

Від'ємний результат подати у прямому двійково-десятковому коді.

 

(1ц1л)(2ц1л) = 35₁₆ = 0011 0101₂ = 53₁₀

(1ц8л)(2ц8л) = 28₁₆ = 0010 1000₂ = 40₁₀

 

Операція 53 - 40

 

53 = 0101 0011

40 = 0100 0000 = B

 

Двійковий обернений код B(дв.о.к.) = 1011 1111,

Двійковий доповняльний код B(дв.д.к.) = 1100 0000,

1001 1001

+ 1100 0000

0101 1001 – двійково-десятковий обернений код B(дв.-дес.о.к.)

0101 1010 – двійково-десятковий доповняльний код B(дв.-дес.д.к.).

 

Додавання доповняльного коду за правилами двійково-десяткової арифметики:

0101 0011

+ 0101 1010

1010 1101

+ 0000 0110 (корекція першої тетради)

1011 0011

+ 0110 0000 (корекція другої тетради)

1 0001 0011

 

Результат 0001 0011 = 13 перенос за межі розрядної сітки вказує на те, що результат

додатній, тобто, 13 - це його абсолютна величина.

 

Операція 40 - 53

 

40 = 0100 0000

53 = 0101 0011 = B

 

Двійковий обернений код B(дв.о.к.) = 1010 1100,

Двійковий доповняльний код B(дв.д.к.) = 1010 1101,

1001 1001

+ 1010 1101

0100 0110 – двійково-десятковий обернений код B(дв.-дес.о.к.)

0100 0111 – двійково-десятковий доповняльний код B(дв.-дес.д.к.).

 

Додавання доповняльного коду за правилами двійково-десяткової арифметики:

0100 0000

+ 0100 0111

1000 0111

 

Результат 1000 0111, відсутність переносу за межі розрядної сітки вказує на те, що результат у доповняльному двійково-десятковому коді від'ємний, щоб отримати його абсолютну величину необхідно перевести результат з доповняльного коду в прямий. Алгоритм переведення такий же, як і для переведення з прямого коду в доповняльний:

інверсія двійкових розрядів 0111 1000;

 

 

додавання 1 молодшого розряду 0111 1001

доповнення до 99 + 1001 1001

0001 0010

прямий двійково-десятковий код 0001 0011.

Результат = -0001 0011 = -13.

 

 

4.5 Виконати операції множення в доповняльному коді двійкових чисел, поданих спочатку в прямому коді:

(+2ц1л) х (+2ц8л),

(-2ц1л) х (+2ц8л),

(+2ц1л) х (-2ц8л),

(-2ц1л) х (-2ц8л).

Попередньо всі числа перевести в доповняльний код. Навести алгоритм множення й таблицю, яка відображає зміни всіх операндів (множеного, множника, лічильника, проміжної суми, окремих розрядів та ознак), які беруть участь у множенні, після виконання кожного з операторів алгоритму. Синтезувати на базі повних однорозрядних суматорів і з використанням елементів базиса Буля функціональну схему матричного помножувача, який виконує операцію множення додатніх чисел (+2ц1л) х (+2ц8л), і навести значення сигналів на входах схеми і на виходах кожного елемента схеми.

 

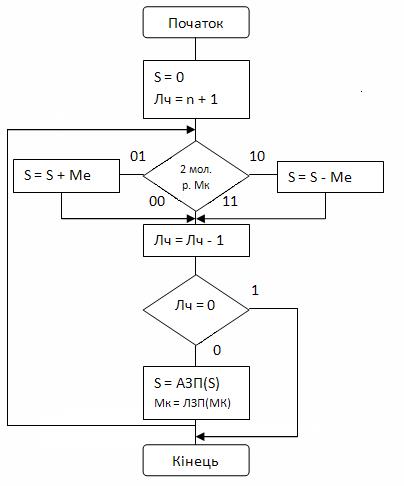
(2ц1л) = 5₁₆ = 0101₂ (2ц8л) = 8₁₆ = 1000₂ (+5) x (+8) = (+40)

Алгоритм множення:

 

 

Лч = n S = 0

 

 

 

На алгоритмі множення введені такі позначеня:

Лч - лічильник;

n - кількість двійкових розрядів множника без знаку;

Мк - множник;

Ме - множене;

S - суматор, після виконання алгоритму в ньому буде знаходитися результат. Розрядність суматора без врахування знаку дорівнює n+m, де m - кількість розрядів множеного без врахування знаку (у прикладі n=m);

мол.р. - молодший розряд;

АЗП - арифметичний зсув праворуч;

ЛЗП - логічний зсув праворуч.

 

(+5) x (+8) = (+40)

 

Mе = 0.101

Мк = 1.000

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000		S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.010		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.001		Лч = Лч - 1
	00.000000			S = S + Ме
00.000000 ^+ 00.101000 00.101000			Мк=ЛЗП (Мк)
00.101000	0.000		Лч = Лч – 1
	00.101000			кінець

 

00.101000_{2 (доп)} = +101000_{2 (пр)} = +40₁₀

 

 

(-5) x (+8) = (-40)

 

Mе = 1.011

Мк = 1.000

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000		S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.010		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.001		Лч = Лч - 1
	00.000000			S = S + Ме
00.000000 ^+ 11.011000 11.011000			S = АЗП(S)
11.011000	0.000		Мк=ЛЗП (Мк)
11.011000			Лч = Лч – 1
	11.011000			кінець

 

11.011000_{2 (доп)} = - 101000_{2 (пр)} = -40₁₀

 

 

(+5) x (-8) = (-40)

 

Mе = 0.101

- Mе = 1.011

- Мк = 1.000

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000		S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.010		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.001		Лч = Лч - 1
	00.000000			S = S + Ме
00.000000 ^+ 11.011000 11.011000			Мк=ЛЗП (Мк)
11.011000	0.000		Лч = Лч – 1
	11.011000			кінець

 

 

11.011000_{2 (доп)} = - 101000_{2 (пр)} = -40₁₀

 

 

(-5) x (-8) = (40)

 

Mе = 1.011

- Ме = 0.101

Мк = 1.000

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000		S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.010		Лч = Лч - 1
	00.000000			S = АЗП(S)
00.000000			Мк = ЛЗП(Мк)
00.000000	0.001		Лч = Лч - 1
	00.000000			S = S + Ме
00.000000 ^+ 00.101000 00.101000			Мк=ЛЗП (Мк)
00.101000	0.000		Лч = Лч – 1
	00.101000			кінець

 

 

00.101000_{2 (доп)} = +101000_{2 (пр)} = +40₁₀

 

Синтез на базі повних однорозрядних суматорів і з використанням елементів базиса Буля функціональної схеми матричного помножувача, який виконує операцію множення додатніх чисел 101 х 111

 

 

4.6 Виконати операцію множення в доповняльному коді методом Бута двійкових чисел, представлених спочатку в прямому коді:

(+2ц1л) х (+2ц8л),

(-2ц1л) х (+2ц8л),

(+2ц1л) х (-2ц8л),

(-2ц1л) х (-2ц8л).

Попередньо всі числа перевести в доповняльний код. Навести алгоритм множення й таблицю, яка відображає зміни всіх операндів (множеного, множника, лічильника, проміжної суми, окремих розрядів та ознак), які беруть участь у множенні, після виконання кожного з операторів алгоритму.

(2ц1л) = 5₁₆ = 0101₂ (2ц8л) = 7₁₆ = 1000₂

Алгоритм множення:

 

 

На алгоритмі множення введені такі позначеня:

Лч - лічильник;

n - кількість двійковихрозрядів множника без знаку;

Мк - множник;

Ме -множене;

S - суматор, після виконання алгоритму в ньому буде знаходитися результат. Розрядність суматора без врахування знаку дорівнює n+m, де m - кількість розрядів множеного без врахування знаку (у прикладі n=m).

2 мол.р. - два молодших розряди;

АЗП - арифметичний зсув праворуч;

ЛЗП - логічний зсув праворуч.

 

 

(+5) x (+8) = (+40)

 

 

Mе = 0.101 - Mе = 1.011 Мк = 1.000

 

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000(0)		Лч = Лч – 1
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100(0)		Лч = Лч - 1
	00.000000			Мк = ЛЗП(Мк)
00.000000	0.010(0)		Лч = Лч - 1
	00.000000			Мк = ЛЗП(Мк)
00.000000	0.001(0)		Лч = Лч - 1
	00.000000			S = S + Ме
00.000000 ^+ 00.101000 00.101000			Мк=ЛЗП (Мк)
00.101000	0.000		Лч = Лч – 1
	00.101000			кінець

 

 

00.101000_{2 (доп)} = +101000_{2 (пр)} = +40₁₀

 

(-5) x (+8) = (-40)

 

Mе = 1.011 - Mе = 0.101 Мк = 1.000

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000	0.100(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000	0.010(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000			Лч = Лч - 1
00.000000	0.001(0)		S = S + Ме
00.000000 ^+ 11.011 11.011000			Мк = ЛЗП(Мк)
	11.011000			Лч = Лч - 1
	11.011000			кінець

 

 

11.011000_{2 (доп)} = - 101000_{2 (пр)} = -40₁₀

 

(+5) x (-8) = (-40)

 

 

Mе = 0.101 - Mе = 1.011 Мк = 1.000

 

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000	0.100(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000	0.010(0)		Лч = Лч - 1
00.000000			Мк = ЛЗП(Мк)
	00.000000			Лч = Лч - 1
00.000000	0.001(0)		S = S - Ме
00.000000 ^+ 11.011 11.011000			Мк = ЛЗП(Мк)
	11.011000			Лч = Лч - 1
	11.011000			кінець

 

 

11.011000_{2 (доп)} = - 101000_{2 (пр)} = -40₁₀

 

(-5) x (-8) = (40)

 

 

Mе = 1.011 - Mе = 0.101 Мк = 1.000

 

 

Лч	S	Мк	мол. р. Мк	Наступна операція
	00.000000	1.000(0)		Лч = Лч – 1
00.000000			Мк = ЛЗП(Мк)
00.000000	0.100(0)		Лч = Лч - 1
	00.000000			Мк = ЛЗП(Мк)
00.000000	0.010(0)		Лч = Лч - 1
	00.000000			Мк = ЛЗП(Мк)
00.000000	0.001(0)		Лч = Лч - 1
	00.000000			S = S - Ме
00.000000 ^+ 00.101000 00.101000			Мк=ЛЗП (Мк)
00.101000	0.000		Лч = Лч – 1
	00.101000			кінець

 

 

00.101000_{2 (доп)} = +101000_{2 (пр)} = +40₁₀

4.7 Виконати операцію ділення 10-розрядного двійкового коду (10)(1ц2л)(1ц8л) на 5-розрядний двійковий код (1)(1ц1л) методом із відновленням залишків. Навести алгоритм ділення й таблицю, яка відображає зміни всіх операндів (діленого, дільника, лічильника, частки, окремих розрядів та ознак), які беруть участь у множенні, після виконання кожного з операторів алгоритму.

(10)(1ц2л)(1ц8л) = 10 0111 0010

(1)(1ц1л) = 1 0011

Алгоритм ділення:

 

 

В алгоритмі використані такі позначення:

Лч - лічильник;

Ч - частка;

n - кількість двійкових розрядів частки без знаку. Для визначення кількості двійкових розрядів частки при діленні цілого числа на ціле необхідно в прямому двійковому коді написати одне під одним ділене і дільник, вирівнявши їх за одиницею у старшому розряді. Тоді кількість розрядів частки n буде дорівнювати різниці довжин вирівняних дільника і діленого, збільшеній на 1;

Дк - дільник;

Де - ділене;

Зн - знак;

# - позначення операції додавання за модулем 2;

S - суматор, на початку виконання алгоритму в ньому буде знаходитися ділене;