
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вважаючи це число шістнадцятковим, перевести його до десяткової, вісімкової та двійкової систем числення з точністю відповідно 3, 3 та 5Содержание книги
Поиск на нашем сайте
Розрядів після коми.
Число: 175,71616=373,44310
373,44310= 010101100101, 100000010110 2
011 111 011, 110 110 011 2= 565,8168
357,82816 = 855,523437510 = 1527,40508 = 1101010111,1000001010002
1.3 Скласти шестизначне число, яке складається з отриманих за допомогою кодової таблиці кодів 1-ої, 2-ої та 8-ої літер прізвища. Вважаючи це число десятковим, перевести його до системи числення залишкових класів із мінімально необхідною кількістю основ 2, 3, 5, 7, 11,.... Після цього зробити зворотне переведення отриманого результату до десяткової системи числення.
Число: 175716.
p1 = 2; p2 = 3; p3 = 5; p4 = 7; p5 = 11; p6 = 13; p7 = 17.
P = p1 * p2 * p3 * p4 * p5 * p6 * p7 = 2 * 3 * 5 * 7 * 11 * 13 *17 = 510510.
175716 mod 2 = 0; 175716 mod 3 = 0; 175716 mod 5 = 1; 175716 mod 7 = 2; 175716 mod 11 = 2; 175716 mod 13 = 8; 175716 mod 17 = 4.
175716 = (0, 0, 1, 2, 2, 8, 4).
B1 = 1*n/2 = 255255;255255 / 2 = 127627 [1] B2 = 1*n/3 = 170170; 170170 / 3 = 56723 [1] B3 = 1*n/5 = 102102; 102102 / 5 = 20420 [2] B3 = 2*n/5 = 204204; 204204 / 5 = 40840 [4] B3 = 3*n/5 = 306306; 306306 / 5 = 61261 [1] B4 = 1*n/7 = 72930; 72930 / 7 = 10418 [4] B4 = 2*n/7 = 145860; 145860 / 7 = 20837 [1] B5 = 1*n/11 = 46410; 46410 / 11 = 4219 [1] B6 = 1*n/13 = 39270; 39270 / 13 = 3020 [10] B6 = 2*n/13 = 78540; 78540 / 13 = 6041 [7] B6 = 3*n/13 = 117810; 117810 / 13 = 9062 [4] B6 = 4*n/13 = 157080; 157080 / 13 = 12083 [1] B7 = 1*n/17 = 30030; 30030 / 17 = 1766 [8] B7 = 2*n/17 = 60060; 60060 / 17 = 3532 [16] B7 = 3*n/17 = 90090; 90090 / 17 = 5299 [7] B7 = 4*n/17 = 120120; 120120 / 17 = 7065 [15] B7 = 5*n/17 = 150150; 150150 / 17 = 8832 [6] B7 = 6*n/17 = 180180; 180180 / 17 = 10598 [14] B7 = 7*n/17 = 210210; 210210 / 17 = 12365 [5] B7 = 8*n/17 = 240240; 240240 / 17 = 14131 [13] B7 = 9*n/17 = 270270; 270270 / 17 = 15898 [4] B7 = 10*n/17 = 300300; 300300 / 17 = 17664 [12] B7 = 11*n/17 = 330330; 330330 / 17 = 19431 [3] B7 = 12*n/17 = 360360; 360360 / 17 = 21197 [11] B7 = 13*n/17 = 390390; 390390 / 17 = 22964 [2] B7 = 14*n/17 = 420420; 420420 / 17 = 24730 [10] B7 = 15*n/17 = 450450; 450450 / 17 = 26497 [1]
B1 = 255255; B2 = 170170; B3 = 306306; B4 = 145860; B5 = 46410; B6 = 157080; B7 = 450450.
(0, 0, 1, 2, 2, 8, 4) = (0 * 255255 + 0 * 170170 + 1 * 306306 + 2 * 145860 + 2 * 46410 + 8 * 157080 + 4 * 450450) (mod 510510) = 3755110 mod 510510 = 181540.
181540 = (0, 0, 1, 2, 2, 8, 4).
Виконати ефективне кодування визначених літер прізвища, при умові, що отримане за допомогою кодової таблиці число - десяткове і говорить про те, скільки разів у "повідомленні" зустрічається дана літера (при цьому, "повідомлення" складається всього з 8 обраних літер). Визначити ефективність проведенного кодування та порівняти її з ентропією джерела повідомлення і ефективністю рівномірного кодування, тобто з випадком, коли довжина коду для кожної літери одна й та сама. За допомогою отриманих кодів ∑скласти повідомлення, яке складається з визначених літер у тій послідовності, в якій вони зустрічаються у прізвищі. Визначити довжину (в бітах) повідомлення при ефективному і рівномірному кодуванні.
К 17 0,06 О 57 0,2 С 26 0,09 Т 46 0,16 І 75 0,26 В 23 0,08 Я 31 0,1 Р 16 0,05 ∑291 ∑100%
H = 0.08*log20.08 + 0.06*log20.06 + 0.05*log20.05) = - (- 0.5 – 0.4 – 0.4 – 0.3509 – 0.33 – 0.2936 – 0.2442 – 0.2238) = - (- 2.7519) = 2.82 Lсер. не еф = Lсер. еф = Lсер. еф. < H < Lсер. не еф.
0001 10 0011 011 11 0010 010 0000 26 біт
010 000 011 110 101 111 001 100 24 біт
Для шістнадцяти розрядного двійкового коду (1ц1л)(2ц1л)(1ц8л)(2ц8л) сформувати код Геммінга (Hamming) і продемонструвати його реакцію на однократний збій. Результати подати у вигляді таблиці.
171616 = 0001 0111 0001 01102
(0) k1 = i3 # i5 # i7 # i9 # i11 # i13 # i15 # i17 # i19 # i21 = 0#0#1#0#1#0#0#1#1#0=0 k2 = i3 # i6 # i7 # i10 # i11 # i14 # i15 # i18 # i19 = 0#0#1#1#1#0#0#0#1=0 k4 = i5 # i6 # i7 # i12 # i13 # i14 # i15 # i20 # i21 = 0#0#1#1#0#0#0#1#0=1 k8 = i9 # i10 # i11 # i12 # i13 # i14 # i15 = 0#1#1#1#0#0#0=1 k16 = i17 # i18 # i19 # i20 # i21 = 1#0#1#1#0=1 Для певного (і) задаємо хибне значення і робимо розрахунки з (К), визначаємо за допомогою формул яке значення (і) ми змінили. Обчислюємо код Геммінга даної формули з хибним значенням. Якщо отриманий код буде =0000 то інформація передалася без помилок. Будь–який інший код буде вказувати на номер розряду, у якому є помилка. K1 = i3 # i5 # i7 # i9 # i11 # i13 # i15 # i17 # i19 # i21= 0#0#1#0#1#0#0#1#1#0=0
K2 = i3 # i6 # i7 # i10 # i11 # i14 # i15 # i18 # i19 =0#0#1#1#1#0#0#0#1=0 K4 = i5 # i6 # i7 # i12 # i13 # i14 # i15 # i20 # i21 = 0#0#1#1#0#0#0#0#0=0 K8 = i9 # i10 # i11 # i12 # i13 # i14 # i15 = 0#1#1#1#0#0#0=1 K16 = i17 # i18 # i19 # i20 # i21 = 1#0#1#0#0=0 K # k = (K16 # k16)(K8 # k8)(K4 # k4)(K2 # k2)(K1 # k1) = (0 # 1)(1 # 1)(0 # 1)(0 # 0)(0 # 0) = 101002
1.6 Для послідовності 16-кових цифр (1ц1л)(2ц1л)(1ц2л)(2ц2л)(1ц3л)(2ц3л)...(2ц7л)(1ц8л)(2ц8л), користуючись картами Карно, визначити всі можливі помилкові коди, які можуть виникати при переході від цифри до цифри. Вхідні дані:(к о с т і в я р), отримано наступні шістнадцяткові цифри: 17 57 26 46 75 23 31 16. Хід роботи: 1. Вхідні дані:1 —> 7 —> 5 —> 7 —> 2 —> 6 —> 4 —> 6 —> 7 —> 5 —> 2 —> 3 —> 3 —> 1 —> 1 —> 6
Визначити класи функцій алгебри логіки, до яких належить задана за допомогою таблиці функція трьох змінних (табл. ТZ.2), і її функціональну повноту. Двійкові коди цифр у графі "f" табл. ТZ.2 потрібно написати вертикально, старший розряд - наверху.
1ц4л – 4 0100 2ц7л – 1 0001
1) Функція на нульовому наборі змінних f(0,0,0) = 0. Отже, функція зберігає константу «0». 2) Функція на одиничному наборі змінних f(1,1,1) = 1. Отже, функція зберігає константу «1». 3) Функція не є монотонною, оскільки при будь-якому зростанні кількості "1" у послідовності сусідніх наборів змінних значення функції зменшується.
4)
Функція не є самодвоїстою, оскільки на третій та четвертій парі протилежних наборів функція не приймає протилежні значення.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 667; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.41.143 (0.011 с.) |

 = - (0.26*log20.26 + 0.2*log20.2 + 0.16*log20.16 + 0.1*log20.1 + 0.09*log0.09 +
= - (0.26*log20.26 + 0.2*log20.2 + 0.16*log20.16 + 0.1*log20.1 + 0.09*log0.09 + = 3
= 3  = 3
= 3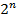 -2 кількість помилкових проміжних станів буде - 2. Кількість можливих послідовностей
n! - 2.
-2 кількість помилкових проміжних станів буде - 2. Кількість можливих послідовностей
n! - 2.



