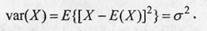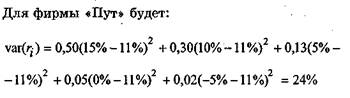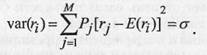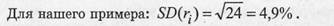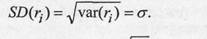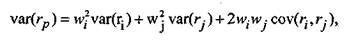Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ожидаемая доходность портфеляСодержание книги Поиск на нашем сайте
В теории портфельного инвестирования исходят из того, что значения доходности отдельной ценной бумаги портфеля являются случайными величинами:
где случайная величина г — доходность; Cf+i — цена продажи в момен— цена покупки в момент времени t. Существуют два подхода к построению распределения вероятностей — сценарный (субъективный) и исторический. При использовании сценарного (субъективного) подхода инвестор определяет и анализирует возможные сценарии развития экономической ситуации в течение холдингового периода, оценивает вероятность каждого результата и ожидаемую при этом доходность ценной бумаги в будущем. Таблица 11.1.1 Распределение вероятностей значений HPR на рынке акций
Ожидаемая доходность (или взвешенная средняя величина доходности) во всех сценариях равна:
В основе исторического подхода лежит предположение о том, что распределение вероятностей будущих (ожидаемых) величин практически совпадает с распределением вероятностей уже наблюдавшихся фактических величин. Следовательно, чтобы получить представление о распределении случайной величины г в будущем, достаточно построить распределение этих величин за какой-то промежуток времени в прошлом. Ожидаемая (или средняя) доходность равна:
где N—число лет, в течение которых велись наблюдения; г. (t = 1, 2,..., N) — значения доходности актива в конце t-то холдингового периода; Р — вероятности данных значений доходности. Пример. Пусть инвестор желает купить акции компании «Пут». Распределение вероятности доходности ее акций определено на основе статистических данных за прошлые периоды (см. табл. 11.1.2). Таблица 11.1.2 Распределение вероятностей доходности акций компании «Пут»
Имеем: Е(п) = 0,50 • 15 + 0,30 • 10 + 0,13 • 5 + + 0,05 • 0 + 0,02 • (-5) = 11% — ожидаемая или средняя доходность акций компании «Пут». Вероятность реализации определяется как отношение временного промежутка, в течение которого наблюдается данное значение доходности, ко всему времени наблюдения.
Ожидаемая доходность портфеля равна средневзвешенному значению ожидаемых значений доходностей ценных бумаг, входящих в портфель: (11.1.2) где Е(гр) — ожидаемая
Определение риска портфеля В качестве меры риска используют вариацию (дисперсию) случайной величины или стандартное отклонение, равное корню квадратному из вариации. Вариация — мера разброса случайной величины вокруг ее среднего значения. В математике — это математическое ожидание квадрата отклонений случайной величины X от ее ожидаемого (среднего) значения Е(Х), равное:
Формула для определения вариации доходности i-ro актива имеет вид:
Стандартное отклонение, имеющее ту же размерность, что и доходность, равно:
Риск инвестиций тем больше, чем больше стандартное отклонение или вариация. Недостатки вариации как меры риска следующие. 1. Вариация учитывает отклонения в обе стороны по отношению к среднему значению. Инвестор же, естественно, не расценивает превышение реальной доходности над ожидаемым результатом как отрицательный результат, а напротив. Поэтому расчет риска с помощью вариации и стандартного отклонения завышает значение риска. В связи с этим Марковец ввел понятие полувариации, однако расчет ее оказался довольно сложен. 2. Вариация не учитывает асимметричность распределения отклонений от среднего значения. В этом случае используются иные методы и параметры типа коэффициента асимметрии. Вариация портфеля из двух активов равна:
где cov)— ковариация доходностей активов i и j. Она отражает степень согласованности (корреляции) в поведении доходностей активов. Ковариация и коэффициент корреляции являются мерами взаимозависимости двух случайных величин. Положительная ковариация означает, что в движении доходности двух ценных бумаг имеется тенденция изменяться в одних и тех же направлениях: если доходность одной акции возрастает (уменьшается), то и доходность другой акции также возрастет (уменьшится). Если же просматривается обратная тенденция, то есть увеличению (уменьшению) доходности акций одной компании соответствует снижение (уменьшение) доходности акций другой компании, то считается, что между доходностя-ми акций этих двух компаний существует отрицательная ковариация.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.186 (0.01 с.) |

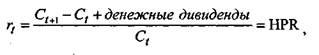
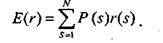
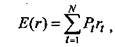 (11.1.1)
(11.1.1)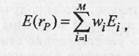 норма доходности портфеля Р за период; Ei — доходность актива i за период; wt — вес актива i в портфеле (доля рыночной стоимости актива i в общей рыночной стоимости всего портфеля); М — число активов в портфеле.
норма доходности портфеля Р за период; Ei — доходность актива i за период; wt — вес актива i в портфеле (доля рыночной стоимости актива i в общей рыночной стоимости всего портфеля); М — число активов в портфеле.