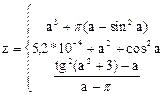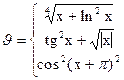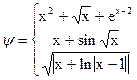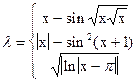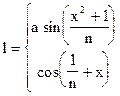Поєднання циклу з розгалудженням.

Обчислити значення функції на відрізку [a,b] з кроком С, згідно з індивідуальним варіантом по таблиці 3.

Таблиця 3.

№	Функція	Умова	а	в	с
		x<-1 -1£x<0 x³0	-2		0,2
		f³1 f<-1 -1£f<1	-3		0,3
		b<0 0£b£1 b>1	-2		0,4
		a£0 0<a<2 a³2	-1		0,2
		2£r£4 r>4 r<2			0,25
		-1£s£1,2 s<-1 s>1,2	-2		0,2
		y>1 0£y£1 y<0	-2		0,2
		y³2 -2<y<2 y£-2	-4		0.5
		x>-0,5 -1£x£-0,5 x<-1	-5		0,5
		x£-1 -1£x<0 x³0	-4		0,5
		x£-0,5 -0,5<x£0,5 x>0,5	-2		0.2
		x<-1 -1£x<1 x³1	-5		0,5
		x<1 1£x£2 x>2			0.2
		x³0 -1<x<0 x£-1	-4		0,5
		x>0,5 0,1£x£0,5 x<0,1	-1		0,1
		x³1 -1<x<1 x£-1	-2		0.2
		x>2 0<x£2 x£0	-3		0,3
		x³1 -1<x<1 x£-1	-2		0.2
		x<0 0£x£1 x>1	-2		0.2
		x>3 0<x£3 x£0	-5		0.5
		x>1 0£x£1 x<0	-2		0.2
		x>1 -1£x£1 x<-1	-3		0,3
		x>0 -3£x£0 x<-3	-4		0.4
		x<-6 -6£x£-1 x>-1	-8		0.5
		x>5 1£x£5 x<1	-1		0,5
		x³0,4 -0,4<x<0,4 x£-0,4	-1		0,1
		x>a x=a x<a			0,5
		x<0,5 x=0,5 x>0,5	0,2		0,1
		x<-0,1 -0,1£x£0,1 x>0,1	-1		0,1

Завдання №8.

Надрукувати таблицю функції, згідно з індивідуальним варіантом.

1. Протабулювати функцiю Y=F(X) на вiдрiзку [a,b] з кроком h i знайти найбiльше та найменше її значення.

2. Надрукувати таблицю значень функцiї Y=F(X) на вiдрiзку [a,b] з кроком h до першого значення Y>Z.

3. Задана функцiя Y=F(X) на вiдрiзку [a,b].Протабулювати її до змiни знака функції.

4. Задана спадна функцiя (X наближається до нескiнченностi, Y-до нуля). Надрукувати таблицю значень функції з кроком h, починаючи з Х=0 i закiнчуючи за умови F(X)<E.

5. Для функції Y=F(X) надрукувати тiльки тi значення, якi задовольняють умовi m £ Ј Y £ Ј M. Аргумент змiнюється вiд a до b з кроком h.

6. Вiдомо, що значення функції Y=F(X) в точцi Х=a вiд'ємне. Надрукувати таблицю значень функції на вiдрiзку [a,b] з кроком h до того значення аргументу, для якого F(X)>0.

7. Нехай Y=F(X) наближається до нуля, коли Х наближається до нескiнченностi. Протабулювати F(X) з кроком h вiд a до того значення, коли F(X)<EРS.

8. Задана функцiя Y=F(X) на вiдрiзку [a,b]. Видати на друк тi значення аргументу, в яких функцiя змінює знаки.

9. Нехай Y=F(X) періодична. Пiдрахувати, скiльки разiв вона перетинає вiсь OX на вiдрiзку [a,b].

10. Нехай функцiя Y=F(X) має на [a,b] один екстремум. Методом повного перебору знайти з точнiстю ЕPS таке значення Х, в якому функцiя досягає екстремуму.

11. Функцiя Y=F(X) неперервна на [a,b]. Знайти всi локальнi екстремуми з точнiстю ЕPS.

12. Нехай Y=F(X) має один екстремум на [a,b]. Знайти його з точнiстю ЕPS, а також найбiльше та найменше значення на [a,b].

13. Для Y=F(X) визначити на [a,b] дiлянки монотонностi.

14. Функцiя Y=F(X) неперервна на [a,b]. Визначити дiлянки зростання.

15. Заданi двi функцiї Y1=F1(X),Y2=F2(X). Визначити спiльнi дiлянки зростання.

16. Заданi функцiї Y1=F1(X) та Y2=F2(X). Визначити на [a,b] найменшу вiдстань мiж ними.

17. Заданi функцiї Y1=F1(X) та Y2=F2(X). Визначити з точнiстю ЕPS точку їх перетину.

18. Визначити, чи має Y=F(X) один екстремум на [a,b].

19. Визначити, скiльки раз на [a,b] перетинається Y1=F1(X) та Y2=F2(X).

20. Визначити, чи перетинаються на [a,b] Y=F(X) та пряма ax+by=c.

21. Заданi Y=F(X) та двi прямi Y1=C та Y2=D. Визначити чи мiститься функцiя на [a,b] мiж цими прямими.

22. Y=F(X) періодично наближається до нуля при Х ® ¥. Визначити кiлькiсть перетинiв Y осi OX на дiапазонi [a,b].

23. Заданi Y=F(X), Y1=С, Y2=D. Визначити максимальне вiдхилення функцiї вiд прямих Y1 та Y2.

24. Знайти найбiльшу вiдстань мiж Y1=F1(X) та Y2=F2(X) на вiдрiзку [a,b].

25. З точнiстю ЕPS знайти всi точки перетину функцiї Y=F(X) та прямої Y=С на вiдрiзку [a,b].

26. З точнiстю ЕPS знайти всi точки перетину Y1=F1(X) та Y2 =F2(X) на вiдрiзку [a,b].

27. З точнiстю ЕPS знайти всi екстремальнi точки функцiї Y=F(X) на вiдрiзку [a,b].

28. Для функцiї Y=F(X) на вiдрiзку [a,b] надрукувати наближене значення її похiдної (dY/h).

29. Для періодичної функцiї Y=F(X) на вiдрiзку [a,b] пiдрахувати кiлькiсть перетинів її з прямою Y=С.

30. З точнiстю EPS пiдрахувати кiлькiсть локальних максимумiв для періодичної Y=F(X) на вiдрiзку [a,b].

 

 

Завдання до РГР по курсу «основи алгоритмізації».

Курс.

Завдання №9.