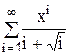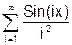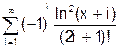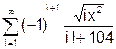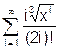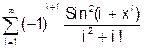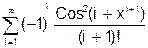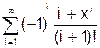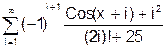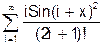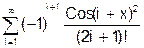Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні обчислювальні процесиСодержание книги Поиск на нашем сайте
1. Обчислити висоти трикутника, знаючи координати його вершин. 2. Матеріальна точка рухається за законом s(t) = at + bt2 - ct3/3, де s(t) - шлях; t - час. Знайти найбільше значення швидкості руху точки. 3. Визначити висоту трикутника, якщо площа трикутника дорівнює S, а основа більше висоти на величину A. 4. Обчислити сторони трикутника АВС, заданого координатами його вершин. 5. Знайти значення функції при х=1
6. Знайти значення функції при х=2
7. Знайти значення функції при довільному х
8. Обчислити вартість розмови, якщо відома кількість хвилин, тариф. 9. Обчислити периметр трикутника по заданих координатах його вершин. 10. Обчислити час падіння тіла t, якщо відома висота h, прискорення g, і початкова швидкість V0.
Завдання №4. АЛГОРИТМИ РОЗГАЛУЖЕНИХ ОБЧИСЛЮВАЛЬНИХ ПРОЦЕСІВ 1. Введіть три числа, виберіть найбільше. 2. Введіть три числа, виберіть найменше. 3. Обчислити значення функції:
y = lg(ax+
4. Обчислити площу трикутника з сторонами А, B, С за формулою Герона. 5. Визначити квадрат знаходження точки за заданими координатами. 6. Знайти квадрат найбільшого із трьох чисел A, B, C і куб найменшого з цих чисел. 7. Визначити, чи значення змінних H і M кратні 3. Якщо обидва значення кратні 3, то обчислити їх суму, інакше обчислити їх різницю. 8. Обчислити значення функції:
y = a Cos2 (аeх) + a Sin2(aex) при x > 7.
9. Визначити мінімальний елемент із чотирьох Х1, X2, X3, X4 та його номер.
10. Обчислити площі різних геометричних фігур і вивести на друк їх назву.
A H/2 якщо n =2; S = (A+B) H/2 якщо n =3; πR2 якщо n =4; πR2 φ/360 якщо n =5. 11. Дано три цілих позитивні числа А, В, С. Обчислити значення функції:
y = ln(A+B) при K=1;
12. Обчислити значення функції:
1,8 ax при x = 1; S = (x-2)2 + 6 при 1< x <2; 3 tg x при x > 5.
13. Упорядкувати три числа X, Y, Z за збільшенням так, щоб змінній A відповідало найменше число, B - середнє, С - найбільше.
Завдання №5. АЛГОРИТМИ АРИФМЕТИЧНИХ ЦИКЛІЧНИХ ОБЧИСЛЮВАЛЬНИХ ПРОЦЕСІВ. Цикли з передумовою. 1. Знайти суму чисел від 1 до 10. 2. Знайти добуток чисел від 1 до 10. 3. Знайти значення інтеграла
4. Обчислити і вивести на друк позитивні значення функції y = sin(nx) - cos(n/x) при n = 1,2,...,50. 5. Визначити з точністю до 0.1 точку перетину функції Y = X – arctgХ – n з віссю Х, змінюючи значення Х від 2 до 5 з кроком 0,1. При перетині осі Х функція змінює знак. 6. Обчислити значення функції:
y = Cos2x+Sin2x, при -5 < х < 5; ab lg(bx), при х > 5,
x змінюється в інтервалі [-10; 10] з кроком 1. 7. Обчислити значення функції:
y = a Cos2 (аeх) + a Sin2(aex) при x > 7.
x змінюється в інтервалі [0; 10] з кроком 0.5. 8. Скласти програму табуляції значень функції у = Сos(x) для аргументу х, який змінюється від 0 до 1800 з кроком 50. 9. Підрахувати суму цифр в числі N. 10. Знайти суму членів ряду s=1+x/5+x/7+x/9+ ….. 11. Обчислити значення суми нескінченого ряду із заданою точністю e згідно із заданим варіантом. S = -
12. Обчислити значення суми нескінченого ряду із заданою точністю e згідно із заданим варіантом. S = x - Цикли з постумовою. 1. Знайти суму чисел від 1 до 10. 2. Знайти добуток чисел від 1 до 10. 3. Знайти значення інтеграла
4. Обчислити і вивести на друк позитивні значення функції y = sin(nx) - cos(n/x) при n = 1,2,...,50. 5. Визначити з точністю до 0.1 точку перетину функції Y = X – arctgХ – n з віссю Х, змінюючи значення Х від 2 до 5 з кроком 0,1. При перетині осі Х функція змінює знак. 6. Обчислити значення функції:
y = Cos2x+Sin2x, при -5 < х < 5; ab lg(bx), при х > 5,
x змінюється в інтервалі [-10; 10] з кроком 1. 7. Обчислити значення функції:
y = a Cos2 (аeх) + a Sin2(aex) при x > 7.
x змінюється в інтервалі [0; 10] з кроком 0.5. 8. Скласти програму табуляції значень функції у = Сos(x) для аргументу х, який змінюється від 0 до 1800 з кроком 50. 9. Підрахувати суму цифр в числі N. 10. Знайти суму членів ряду s=1+x/5+x/7+x/9+ ….. 11. Обчислити значення суми нескінченого ряду із заданою точністю e згідно із заданим варіантом. S = - 12. Обчислити значення суми нескінченого ряду із заданою точністю e згідно із заданим варіантом. S = x - Завдання №6. АЛГОРИТМИ АРИФМЕТИЧНИХ ЦИКЛІЧНИХ ОБЧИСЛЮВАЛЬНИХ ПРОЦЕСІВ. Цикли з невідомою кількістю повторень. Визначити суму нескiнченного ряду з точнiстю Е=0.0004, згідно з індивідуальним варіантом по таблиці 2. Роздрукувати всi члени ряду, що входять в склад суми. Таблиця 2.
Завдання №7.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.009 с.) |

 .
. .
. .
.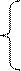 πx2 – 7/x2 при а < 1,3;
πx2 – 7/x2 при а < 1,3; ах3 + 7
ах3 + 7  при а = 1,3;
при а = 1,3;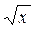 ) при a > 1,3.
) при a > 1,3. lg3 a2 +
lg3 a2 +  / e x при x < 3;
/ e x при x < 3;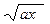 + 1/x при 3 < x < 7;
+ 1/x при 3 < x < 7;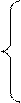 A B якщо n =1;
A B якщо n =1;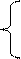 e m+A/B при K=0;
e m+A/B при K=0; при K=2.
при K=2. 1,5 Cos2 x при x < 1;
1,5 Cos2 x при x < 1;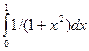 .
. ae Sin x +Cosx, при х < -5;
ae Sin x +Cosx, при х < -5; lg3 a2 +
lg3 a2 + 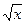 / e x при x < 3;
/ e x при x < 3;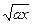 + 1/x при 3 < x < 7
+ 1/x при 3 < x < 7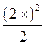 +
+  -
- 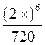 +...; x = 0.2; e =
+...; x = 0.2; e = 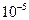
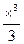 +
+  -
-  +...;
+...;  x = 0.1; e =
x = 0.1; e = 
 lg3 a2 +
lg3 a2 + 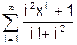
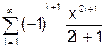
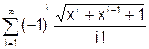
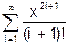

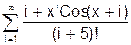
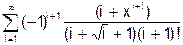

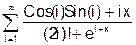
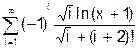
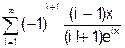


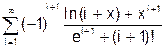
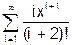
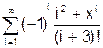 0,4
0,4