
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношений между различными видами рекомбинацииСодержание книги
Поиск на нашем сайте
При наличии нескольких механизмов рекомбинации суммарное время жизни t определяется по следующей формуле.
где ti - время жизни при i-ом механизме рекомбинации. Таким образом, при одновременном действии нескольких механизмов рекомбинации результирующее время жизни будет определяться наименьшим временем жизни, соответствующим наиболее вероятному механизму рекомбинации. Относительный вклад различных видов рекомбинации в значительной степени зависит от отношения ширины запрещенной зоны к тепловой энергии (кТ), глубины залегания и концентрации рекомбинационных центров, концентрации равновесных носителей заряда, температуры и внешних условий. Разработанная в настоящее время техника очистки полупроводниковых материалов не позволяет избежать преобладающего влияния рекомбинации на ловушках при D Е >20 кТ (около 0,5 эВ при комнатной температуре). Прямая рекомбинация играет существенную роль в прямозонных полупроводниках с малой шириной запрещенной зоны и ее вероятность возрастает при повышении температуры. Рекомбинация через ловушки Теорию рекомбинации через ловушки разработали Шокли, Рид и Холл. Они исследовали простейшую модель полупроводника, который содержит примесь только одного сорта, дающую один рекомбинационный уровень Et в запрещенной зоне (рис.3). Рассмотрим эту теорию в предположении, что концентрация ловушек Nt мала. В этом случае можно считать, что Dn = Dр. Если Nt сравнимо с Dn и Dр то часть избыточных носителей захватывается ловушками, при этом Dn ≠ Dр и время жизни tn ≠ tp.
Рис.3. Переходы электронов и дырок при рекомбинации через ловушки; 1- захват электрона:2 - эмиссия электрона; 3- захват дырки: 4 ~ эмиссия дырки. Скорость захвата rn электронов пропорциональна концентрации свободных электронов n и концентрации пустых ловушек Nt(1-ft).
где cn - коэффициент захвата электрона пустой ловушкой; ft - вероятность того, что ловушка занята электроном. Скорость эмиссии электронов с ловушек обратно в зону проводимости пропорциональна концентрации электронов на ловушках.
где dn - коэффициент эмиссии электрона с ловушки. В состоянии термодинамического равновесия r n0= gn0 и
где индекс «0» показывает, что значения n и ft – равновесные. Предположим, что в равновесном состоянии ft0 совпадает с функцией распределения Ферми-Дирака
Для невырождеиного полупроводника
Поэтому
Обозначим через
После термализации неравновесных носителей характер взаимодействия носителей с ловушками и тепловая генерация с ловушек не зависят от того, является данный электрон (дырка) равновесным или неравновесным. В неравновесном состоянии результирующая скорость захвата электронов ловушками Rn = rn - gn будет равна
Результирующая скорость захвата дырок ловушками Rp = rp - gp вычисляется аналогично.
где В отсутствии процессов прилипания и захвата при рекомбинации неравновесных носителей парами имеем: Rn = Rn = R. Это условие определяет функцию распределения ft которая отличается от равновесной функции распределения.
Подставив ft в выражение для Rn или Rp, получим скорость рекомбинации после выключения инжекции.
Поскольку n1p1 = ni 2, n = n 0+D n, p = p 0+D n, получим для малого уровня инжекции
Согласно определению времени жизни (3) и (4), находим
Обозначим
Тогда время жизни пары электрон-дырка будет равно
Таким образом, время жизни зависит от сечения захвата и концентрации ловушек (через tp0 и tn0) концентрации легирующей примеси (через n0 и p0), положения уровня ловушек (через n1 и p1), уровня инжекции (через D n) и температуры (через n1, p1, n0, p0). Однако, строго говоря, концентрация незаполненных ловушек Nt при рекомбинации является переменной величиной и поэтому уравнение, описывающее рекомбинационный процесс становится нелинейным, так как Nt является функцией D n (t).
Изменение концентрации заполненных ловушек Ntf определяется следующим уравнением.
Для случая монополярной инжекции n = n 0+D n, а f = f0 + D f. Учитывая, что n0 (1- f)- число захваченных электронов равно числу электронов n 1 f 0, которые могут генерироваться с уровня Et, получим для уравнения (7а).
Учитывая, что N D f =D n получим окончательно
где Nt0 = Nt (1- f 0) - равновесная концентрация пустых ловушек, an - скорость захвата в единицу времени, а так как скорость рекомбинации rn =D n / tn, то, следовательно, коэффициент при D n есть tn -1. Таким образом, при указанных условиях процесс релаксации имеет экспоненциальный характер, а главное - время релаксации tn становится постоянной величиной.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.006 с.) |

 ,
,

 ,
,
 ,
,
 ,
,
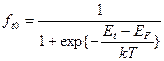 ,
,
 и
и  .
.
 ,
,
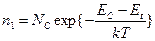 концентрацию электронов в зоне проводимости, когда уровень Ферми совпадает с уровнем ловушки. Тогда
концентрацию электронов в зоне проводимости, когда уровень Ферми совпадает с уровнем ловушки. Тогда .
.
 .
.
 ,
,
 - концентрация дырок в валентной зоне, когда уровень Ферми совпадает с уровнем ловушки.
- концентрация дырок в валентной зоне, когда уровень Ферми совпадает с уровнем ловушки. .
.
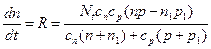 .
.
 ,
,
 .
.
 ,
,  .
.
 .
.
 .
.
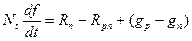 .
.
 .
.
 ,
,



