
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноканальная смо с отказамиСодержание книги Поиск на нашем сайте
Рассмотрим простейшую из всех задач теории массового обслуживания – задачу о функционировании одноканальной СМО с отказами. Пусть система массового обслуживания состоит только из одного канала (n=1) и на нее поступает пуассоновский поток заявок с интенсивностью λ, зависящей, в общем случае, от времени: λ = λ (t) (3.1) Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени Tоб, распределенного по показательному закону с параметром μ:
f(t) = μ e-μt (t>0). (3.2)
Из этого следует, что «поток обслуживаний» - простейший, с интенсивностью μ. Чтобы представить
Требуется найти: 1) абсолютную пропускную способность СМО (А); 2) относительную пропускную способность СМО (q).
Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний: S0 – свободен, S1 – занят. Граф состояний системы показан на рис. 1. Из состояния S0 в S1 систему, очевидно, переводит поток заявок с интенсивностью λ; из S1 и S0 – «поток обслуживании» с интенсивностью μ. Обозначим вероятности состояний p0(t) и р1(t). Очевидно, для любого момента t: p0(t) + р1(t) = 1 (3.3) Составим дифференциальные уравнения Колмогорова для вероятностей состояний согласно правилу, данному в предыдущем разделе. Имеем:
Из двух уравнений (3.4) одно является лишним, так как p0 и р1 связаны соотношением (3.3). Учитывая это, отбросим второе уравнение, а в первое подставим вместо р1 его выражение (1– p0):
или
Это уравнение естественно решать при начальных условиях: p0 (0)=1, p1 (0)=0 (в начальный момент канал свободен). Линейное дифференциальное уравнение (3.5) с одной неизвестной функцией p0 легко может быть решено не только для простейшего потока заявок (λ = const), но и для случая, когда интенсивность этого потока со временем меняется (λ=λ(t)). He останавливаясь на последнем случае, приведем решение уравнения (3.5) только для случая λ= const:
канал заведомо свободен (p0 (0)=1). С увеличением t вероятность p0 уменьшается и в пределе (при t →∞) равна Нетрудно убедиться, что для одноканальной СМО с отказами ее вероятность p0 есть не что иное, как относительная пропускная способность q. Действительно, p0 есть вероятность того, что в момент t канал свободен, иначе вероятность того, что заявка, пришедшая в момент t, будет обслужена. А значит, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно p0: q = p0. В пределе, при t →∞, когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно: q = Зная относительную пропускную способность q, легко найти абсолютную A. Они связаны очевидным соотношением: А = λq. (3.8) В пределе, при t →∞, абсолютная пропускная способность тоже установится и будет равна A = Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа: Ротк = 1 – q. (3.10) Вероятность отказа Ротк есть не что иное, как средняя доля необслуженных заявок среди поданных. В пределе, при t →∞, Ротк = 1 –
Пример. Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов λ = 0,8 (вызовов в минуту). Средняя продолжительность разговора tоб = 1,5 мин. Все потоки событий – простейшие. Определить предельные (при t →∞) значения: 1) относительной пропускной способности q; 2) абсолютной пропускной способности А; 3) вероятности отказа Ротк. Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый разговор длился в точности 1,5 мин, и разговоры следовали бы один за другим без перерыва. Решение. Определяем параметр μ потока обслуживаний: μ =1/ tоб = 1/1,5 = 0,667. По формуле (3.6) получаем относительную пропускную способность СМО: q = Таким образом, в установившемся режиме система будет обслуживать около 45% поступающих вызовов. По формуле (3.9) находим абсолютную пропускную способность: А = λq = 0,8·0,455 » 0,364, т. е. линия способна осуществить в среднем 0,364 разговора в минуту. Вероятность отказа: Ротк = 1 – q = 0,545, значит около 55% поступивших вызовов будет получать отказ. Номинальная пропускная способность канала: Aном = 1/ tоб = 0,667 (разговора в минуту), что почти вдвое больше, чем фактическая пропускная способность, получаемая с учетом случайного характера потока заявок и случайности времени обслуживания.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 3040; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.79.187 (0.005 с.) |


 (3.4)
(3.4)
 (3.5)
(3.5) (3.6)
(3.6) Зависимость величины p0 от времени имеет вид изображенный на рис. 2. В начальный момент (при t =0)
Зависимость величины p0 от времени имеет вид изображенный на рис. 2. В начальный момент (при t =0)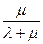 . Величина p0 (t), дополняющая p0 (t) до единицы, изменяется как показано на том же рис. 2.
. Величина p0 (t), дополняющая p0 (t) до единицы, изменяется как показано на том же рис. 2.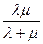 . (3.9)
. (3.9) (3.11)
(3.11) = 0,455.
= 0,455.


