
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смо с ограниченным временем ожиданияСодержание книги
Поиск на нашем сайте
До сих пор мы рассматривали СМО с ожиданием, ограниченным только длиной очереди (числом m заявок, одновременно находящихся в очереди). В такой СМО заявка, раз ставшая в очередь, уже не покидает ее и «терпеливо» дожидается обслуживания. На практике нередко встречаются СМО другого типа, в которых заявка, подождав некоторое время, может уйти из очереди (так называемые «нетерпеливые» заявки).
Рис.8
Рассмотрим СМО подобного типа, оставаясь в рамках марковской схемы. Предположим, что имеется n -канальная СМО с ожиданием, в которой число мест в очереди не ограничено, но время пребывания заявки в очереди ограничено некоторым случайным сроком Точ со средним значением
Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским. Найдем для него вероятности состояний. Будем снова нумеровать состояния системы по числу заявок, связанных с системой – как обслуживаемых, так и стоящих в очереди: S0 – все каналы свободны, S1 – занят один канал, остальные свободны, ....... Sk – заняты k каналов, остальные свободны, ....... Sn – заняты все n каналов, Sn+1 – заняты все n каналов; одна заявка стоит в очереди, ....... Sn+r – заняты все n каналов, r заявок стоят в очереди, ....... и т. д. Граф состояний системы показан на рис. 8. Разметим этот граф, т. е. проставим у стрелок соответствующие интенсивности. Снова, как и раньше, у всех стрелок, ведущих слева направо, будет стоять интенсивность потока заявок λ. Для состояний без очереди у стрелок, ведущих из них справа налево, будет, как и раньше, стоять суммарная интенсивность потока обслуживании всех занятых каналов. Что касается состояний с очередью, то у стрелок, ведущих из них справа налево будет стоять суммарная интенсивность потока обслуживании всех n каналов n μ, плюс соответствующая интенсивность потока уходов из очереди. Если в очереди стоят r заявок, то суммарная интенсивность потока уходов будет равна r ν. Как видно из графа, перед нами опять схема гибели и размножения; применяя общие выражения для предельных вероятностей состояний в этой схеме, напишем:
или, вводя обозначения: ρ = λ / μ, β = ν / μ,
Если длина очереди не ограничена заранее никаким числом и заявки «терпеливы» (не уходят из очереди), то стационарный предельный режим существует только в случае ρ < n (при ρ ≥ n соответствующая бесконечная геометрическая прогрессия расходится, что физически соответствует неограниченному росту очереди при t →∞). Напротив, в СМО с «нетерпеливыми» заявками, уходящими рано или поздно из очереди, установившийся режим обслуживания при t →∞ достигается всегда, независимо от приведенной интенсивности потока заявок ρ. Это следует из того, что ряд в знаменателе первой формулы (7.1) сходится при любых положительных значениях ρ и β. Для СМО с «нетерпеливыми» заявками понятие «вероятность отказа» не имеет смысла – каждая заявка становится в очередь, но может и не дождаться обслуживания, уйдя раньше времени. Относительную пропускную способность q такой СМО можно подсчитать следующим образом. Очевидно, обслужены будут все заявки, кроме тех, которые уйдут из очереди досрочно. Подсчитаем, какое в среднем число заявок покидает очередь досрочно. Для этого вычислим среднее число заявок в очереди:
На каждую из этих заявок действует «поток уходов» с интенсивностью ν. Значит, из среднего числа A = λ– заявок. Относительная пропускная способность СМО будет
Среднее число занятых каналов z по-прежнему получим, деля абсолютную пропускную способность на μ:
Это позволяет вычислить среднее число заявок в очереди
а входящее в эту формулу среднее число занятых каналов можно найти как математическое ожидание случайной величины Z, принимающей значения 0,1, 2,.... n с вероятностями р0, р1, р2,..., [1 – (p0 + p1 +…+ pn-1)]:
= р1 + 2 р2 + … + n [1 – (p0 + p1 +…+ pn-1)]. (7.7)
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.006 с.) |


 оч, таким образом, на каждую заявку, стоящую в очереди; действует как бы «поток уходов» с интенсивностью
оч, таким образом, на каждую заявку, стоящую в очереди; действует как бы «поток уходов» с интенсивностью

 (7.1)
(7.1) Отметим некоторые особенности рассмотренной СМО с «нетерпеливыми» заявками по сравнению с ранее рассмотренной СМО с «терпеливыми» заявками.
Отметим некоторые особенности рассмотренной СМО с «нетерпеливыми» заявками по сравнению с ранее рассмотренной СМО с «терпеливыми» заявками. .
.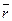 заявок в очереди в среднем будет уходить, не дождавшись обслуживания,
заявок в очереди в среднем будет уходить, не дождавшись обслуживания,  заявок в единицу времени; всего в единицу времени в среднем будет обслужено
заявок в единицу времени; всего в единицу времени в среднем будет обслужено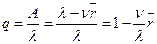 (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6) = 0· р0 + 1· р1 + 2· р2 + … + n ·[1 – (p0 + p1 +…+ pn-1)] =
= 0· р0 + 1· р1 + 2· р2 + … + n ·[1 – (p0 + p1 +…+ pn-1)] =


