
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоканальная смо с отказамиСодержание книги Поиск на нашем сайте
Рассмотрим n -канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, связанных с системой). Состояния будут: S0 – все каналы свободны, S1, – занят ровно один канал, остальные свободны, .... Sk – заняты ровно k каналов, остальные свободны, .... Sn – заняты все n каналов. Граф состояний СМО представлен на рис.3. Разметим граф, т. е. проставим у стрелок интенсивности соответствующих потоков событий. По стрелкам слева направо систему переводит один и тот же поток – поток заявок с интенсивностью λ. Если система находится в состоянии Sk (занято k каналов) и пришла новая заявка, система переходит (перескакивает) в состояние Sk+1.
Рис.3.
Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево. Пусть система находится в состоянии S1 (занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в S0; значит, поток событий, переводящий систему по стрелке S1→S0, имеет интенсивность μ. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживании, переводящий систему по стрелке S2→S1 будет вдвое интенсивнее (2μ); если занято k каналов – в k раз интенсивнее (k μ). Проставим соответствующие интенсивности у стрелок, ведущих справа налево. Из рис.3 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса «гибели и размножения», рассмотренного нами в предыдущем разделе. Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:
Уравнения (4.1) называются уравнениями Эрланга. Естественными начальными условиями для их решения являются: p0(0)=1; p1(0) = p2(0) =... = pn(0) = 0 (в начальный момент система свободна). Интегрирование системы уравнений (4.1) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно, на АВМ или ЭЦВМ. Такое решение дает нам все вероятности состояний p0(t), p1(t), p2(t),... pn(t) как функции времени. Естественно, нас больше всего будут интересовать предельные вероятности состояний p0, p1, p2,... pn, характеризующие установившийся режим работы СМО (t →∞). Для нахождения предельных вероятностей воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения в предыдущем разделе. Согласно этому решению,
В этих формулах интенсивность потока заявок λ и интенсивность потока обслуживании (для одного канала) μ не фигурируют по отдельности, а входят только своим отношением λ /μ. Обозначим это отношение λ /μ = ρ и будем называть величину ρ «приведенной интенсивностью» потока заявок. Физический смысл ее таков: величина ρ представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки. С учетом этого обозначения, формулы (4.2) примут вид:
Формулы (4.3) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров λ, μ и n (λ – интенсивность потока заявок, μ – интенсивность обслуживания, n – число каналов СМО). Зная все вероятности состояний можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А Действительно, заявка получает отказ, если приходит в момент, когда все n каналов заняты. Вероятность этого равна Ротк = pn = Вероятность того, что заявка будет принята к обслуживанию (она же относительная пропускная способность q) дополняет Ротк до единицы: q = 1– pn (4.5) Абсолютная пропускная способность: A = λq = λ ( 1– pn) (4.6) Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число Величину
как математическое ожидание дискретной случайной величины, принимающей значения 0, 1,..,, п с вероятностями p0, p1, p2,... pn. Однако значительно проще выразить среднее число занятых каналов через абсолютную пропускную способность A, которую мы уже знаем. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу времени μ, заявок; среднее число занятых каналов получится делением А на μ:
или, переходя к обозначению λ /μ = ρ
Пример. Повторяются условия примера предыдущего параграфа (λ = 0,8, μ = 0,667), однако вместо одноканальной СМО (n = 1) рассматривается трехканальная (n = 3), т. е. число линий связи увеличено до трех. Найти вероятности состояний, абсолютную и относительную пропускную способности, вероятность отказа и среднее число занятых каналов. Решение. Приведенная интенсивность потока заявок: ρ = λ/μ = 0,8/0,667 = 1,2 По формулам Эрланга (4.3) получаем: p1= p2= p3= p0 = Вычисляем вероятность отказа: Ротк = Рз = 0,090. Относительная и абсолютная пропускные способности равны: q = 1 – р3 = 0,910; A = λ q = 0,8·0,910 = 0,728. Среднее число занятых каналов:
Т. е. при установившемся режиме работы СМО в среднем будет занят один с небольшим канал из трех – остальные два будут простаивать. Этой ценой добывается сравнительно высокий уровень эффективности обслуживания – около 91% всех поступивших вызовов будет обслужено
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.30.14 (0.007 с.) |

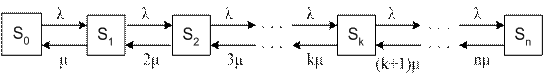
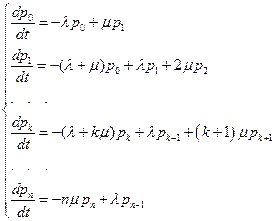 (4.1)
(4.1)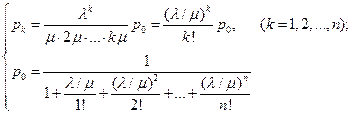 (4.2)
(4.2)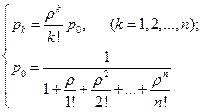 (4.3)
(4.3)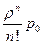 . (4.4)
. (4.4) .
.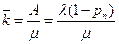 ,
,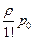 = 1,2 p0,
= 1,2 p0,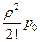 = 0,72 p0
= 0,72 p0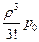 = 0,288 p0
= 0,288 p0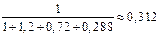 ;
;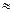 1,09,
1,09,


