
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоканальная смо с ожиданиемСодержание книги Поиск на нашем сайте
Рассмотрим n-канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью l; интенсивность обслуживания (для одного канала) μ; число мест в очереди m. Состояния системы будем нумеровать по числу заявок, связанных с системой: S0 – все каналы свободны, S1 – занят один канал, остальные свободны, ....... Sk – заняты k каналов, остальные свободны, ....... Sn – заняты все n каналов, Sn+1 – заняты все n каналов; одна заявка стоит в очереди, ....... Sn+r – заняты все n каналов, r заявок стоят в очереди, ....... Sn+m – заняты все n каналов, т заявок стоят в очереди,
Граф состояний приведен на рис. 6. У каждой стрелки проставлены соответствующие интенсивности потоков событий. Действительно, по стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью l; по стрелкам справа налево систему переводит поток обслуживании, интенсивность которого равна μ, умноженному на число занятых каналов.
Рис. 6 Граф на рис. 5.6 представляет собой схему «гибели и размножения», для которой решение в общем виде уже получено. Напишем выражения для предельных вероятностей состояний, сразу же обозначая ρ = λ/μ:
или, суммируя геометрическую прогрессию со знаменателем ρ/n (подчеркнутые члены):
Таким образом, все вероятности состояний найдены. Найдем некоторые характеристики эффективности обслуживания. Поступившая заявка получает отказ, если заняты все n каналов и все m мест в очереди: Pотк = Относительная, пропускная способность, как всегда, дополняет вероятность отказа до единицы: q = 1– Pотк = Абсолютная пропускная способность СМО будет равна: A = λ q= λ Найдем среднее число занятых каналов. Для СМО с отказами оно совпадало со средним числом заявок, находящихся в системе. Для СМО с очередью среднее число занятых каналов не совпадает со средним числом заявок, находящихся в системе: последняя величина отличается от первой на среднее число заявок, находящихся в очереди. Сохраним обозначение
или
Среднее число заявок в очереди можно вычислить непосредственно, как математическое ожидание дискретной случайной величины, умножая любое возможное число заявок на вероятность того, что именно это число заявок будет в очереди, и складывая результаты:
Введем обозначение ρ/ n = χ и перепишем (6.5) в виде:
Теперь найдем среднее время ожидания заявки в очереди: Если заявка застанет не все каналы занятыми, ей вообще не придется ждать (соответствующие члены в математическом ожидании отбросим, как равные нулю). Если заявка придет в момент, когда заняты все n каналов, а очереди нет, ей придется ждать в среднем время, равное 1/ n μ (потому что поток освобождений n каналов имеет интенсивность n μ). Если заявка застанет все каналы занятыми и одну заявку перед собой в очереди, ей придется в среднем ждать время 2/ n μ (по 1/ n μ на каждую впереди стоящую заявку) и т. д. Если заявка застанет в очереди r заявок, ей придется ждать в среднем время r / n μ. Если вновь пришедшая заявка застанет в очереди уже m заявок, то она вообще не будет ждать (но и не будет обслуживаться). Среднее время ожидания найдем, умножая каждое из этих значений на соответствующую вероятность:
Так же, как и в случае одноканальной СМО с ожиданием, замечаем, что это выражение отличается от выражения для средней длины очереди (6.5) только множителем 1/ρμ, = 1/l,, т. е.
Подставляя сюда выражение для
Среднее время пребывания заявки в системе, так же, как и для одноканальной СМО, отличается от среднего времени ожидания на среднее время обслуживания, умноженное на относительную пропускную способность:
Пример 1. Автозаправочная станция (АЗС) с двумя колонками (n = 2) предназначена для обслуживания машин. Поток машин, прибывающих на АЗС, имеет интенсивность l = 2 (машины в минуту); среднее время обслуживания одной машины.
Площадка у АЗС может вместить очередь не более m = 3 (машин). Машина, прибывшая в момент, когда все три места в очереди заняты, покидает АЗС (получает отказ). Найти характеристики СМО: - вероятность отказа, - относительную и абсолютную пропускную способности, - среднее число занятых колонок, - среднее число машин в очереди, - среднее время ожидания и пребывания машины на АЗС. Решение. Имеем: n = 2, m = 3, l = 2, μ = 1/ По формулам (6.1) находим:
Вероятность отказа: Pотк = Относительная пропускная способность: q =1 – Pотк = 0,488 Абсолютная пропускная способность: А = q l = 0,976 (машины в минуту). Среднее число занятых каналов (колонок):
(т. е. обе колонки почти все время заняты). Среднее число машин в очереди находим по формуле (6.7):
Среднее время ожидания в очереди – по формуле (6.9):
Среднее время пребывания машины на АЗС (включая время обслуживания):
Выше мы рассмотрели n -канальную СМО с ожиданием, когда в очереди одновременно могут находиться не более n заявок. Так же, как и в предыдущем параграфе, посмотрим, что будет, если длина очереди не ограничена каким-то числом т, а может быть сколь угодно большой. Граф состояний в этом случае – бесконечный (см. рис.7).
Рис. 7 Вероятности состояний получим из формул (6.1) предельным переходом (при m →∞). Заметим, что сумма соответствующей геометрической прогрессии сходится при χ = ρ/ n < 1 и расходится при χ ≥ 1; соответственно, установившийся режим будет существовать при χ<1, а при χ>1 очередь будет бесконечно возрастать. Допустим, что χ<1 и устремим в формулах (6.1) величину m к бесконечности. Получим выражения для предельных вероятностей состояний:
Так как каждая заявка рано или поздно будет обслужена, то характеристики пропускной способности СМО равны: Pотк = 0, q = 1, A = λ q =λ. Среднее число заявок в очереди получим при m →∞ из (6.7):
а среднее время ожидания – из (6.10):
Среднее число занятых каналов
а среднее число заявок, связанных с СМО – как среднее число заявок в очереди плюс среднее число заявок, находящихся под обслуживанием (среднее число занятых каналов):
Пример 2. Автозаправочная станция с двумя колонками (n = 2) обслуживает поток машин с интенсивностью λ = 0,8 (машин в минуту). Среднее время обслуживания одной машины
В данном районе нет другой АЗС, так что очередь машин перед АЗС может расти практически неограниченно. Найти характеристики СМО. Решение. Имеем: n = 2, l = 0,8, μ = 1/ Поскольку χ < 1, очередь не растет безгранично и имеет смысл говорить о предельном стационарном режиме работы СМО. По формулам (6.11) находим вероятности состояний:
p1 = 1,6 p0 p3 = Среднее число занятых каналов найдем, разделив абсолютную пропускную способность СМО А =λ=0,8 на интенсивность обслуживания μ= 0,5:
Вероятность отсутствия очереди у АЗС будет:
p0 + p1 + p2 Среднее число машин в очереди:
Среднее число машин на АЗС:
Среднее время ожидания в очереди:
Среднее время пребывания машины на АЗС:
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.205 (0.011 с.) |





 (6.1)
(6.1) (6.2)
(6.2) .
. (6.3)
(6.3) для среднего числа заявок, связанных с системой, а среднее число занятых каналов обозначим
для среднего числа заявок, связанных с системой, а среднее число занятых каналов обозначим  . Каждый занятый канал обслуживает в среднем μ заявок в единицу времени; вся же СМО обслуживает в среднем А заявок в единицу времени. Деля одно на другое, получим:
. Каждый занятый канал обслуживает в среднем μ заявок в единицу времени; вся же СМО обслуживает в среднем А заявок в единицу времени. Деля одно на другое, получим:
 (6.4)
(6.4) . (6.5)
. (6.5) (6.6)
(6.6) Заметим, что выражение в скобках есть не что иное, как уже вычисленная нами в предыдущем параграфе сумма (5.10), где вместо ρ поставлено χ. Пользуясь этой формулой и подставляя результат в (6.6), получим:
Заметим, что выражение в скобках есть не что иное, как уже вычисленная нами в предыдущем параграфе сумма (5.10), где вместо ρ поставлено χ. Пользуясь этой формулой и подставляя результат в (6.6), получим: . (6.7)
. (6.7)
 Складывая среднее число заявок в очереди
Складывая среднее число заявок в очереди 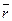 и среднее число занятых каналов
и среднее число занятых каналов  ож. Сделаем ряд гипотез о том, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.
ож. Сделаем ряд гипотез о том, в каком состоянии застанет систему вновь пришедшая заявка и сколько времени ей придется ждать обслуживания.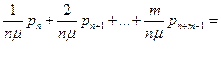

 . (6.9)
. (6.9) . (6.10)
. (6.10) .
.

 = 2,18/2 = 1,09 (мин).
= 2,18/2 = 1,09 (мин).
 (6.12)
(6.12) , (6.13)
, (6.13) . (6.14)
. (6.14)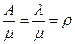 , (6.15)
, (6.15) ,
,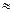 0,178, p2 =1,28 p0
0,178, p2 =1,28 p0  , p4 =
, p4 =  и т.д.
и т.д.



