Понятия о форме и размерах земли

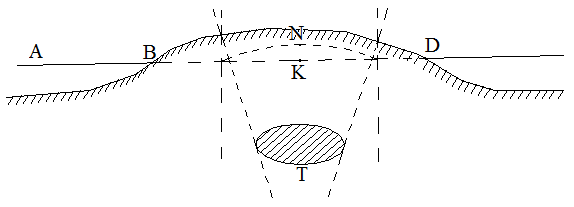
Наша Земля близка по форме к сфероиду вращения, но ввиду неравномерностей она не может быть телом строгой математической формы.

Различают:

1) действительную (физическую) фигуру Земли, ограниченную реальной физической поверхностью Земли;

2) фигуру Земли, ограниченную основной уровенной поверхностью, называемую геоидом.

Уровенная поверхность – это замкнутая поверхность, которая получается путем продолжения поверхности океанов под материками в спокойном состоянии, и которая в каждой своей точке перпендикулярна к направлению действия силы тяжести. Такая поверхность называют основной уровенной поверхностью или поверхностью геоида.

Поверхность геоида всюду выпукла. Направления силы тяжести не пересекаются в центре Земли, так как горные породы разной плотности расположены в земле неравномерно. Вследствие этого фигура геоида весьма сложна и зависит от внутреннего строения Земли. Выясним это на следующем примере;

Пусть в верхних слоях литосферы расположено некоторое физическое тело Т, имеющее большую плотность, чем окружающие его горные породы. Под действием избыточного напряжения тела Т отвесные линии в точках С и С’ окажутся смещенными в направлении к телу Т, поэтому уровенная поверхность пройдет не по дуге ВКД, а по кривой BNД и не будет совпадать с уровнем Мирового океана (рисунок 1).

Рисунок 1- Уровенная поверхность

 

В свое время задача определения фигуры Земли формировалась как задача определения фигуры геоида. Однако выяснилось, что точное определение фигуры геоида является трудноосуществимой задачей и в настоящее время являющейся, пока нерешенной, т. к. распределение плотностей в теле Земли с достаточной полной пока неизвестно

Референц-эллипсоид Ф. Н. Красовского

Препятствия, возникшие при решении задачи определения фигуры Земли, были все же успешно устранены введением понятия квазигеоида (мнимого геоида), совпадающего с геоидом на океанах и открытых морях и весьма мало (менее 2м) отступающего от поверхности геоида на суше.

Действительная фигура Земли, а также фигура Земли в виде геоида или квазигеоида не может быть выражена ни одной из поверхностей, рассматриваемых в математике.

Наиболее близкой к геоиду является математическая поверхность – эллипсоид вращения, называемый земным эллипсоидом.

Параметры:

а – большая и в - малая полуоси эллипсоида. α =

α - сжатие эллипсоида.

Эллипсоид, имеющий наибольшую близость к фигуре Земли в целом, называется общим земным эллипсоидом.

Референц-эллипсоид – это эллипсоид, имеющий строго определенные размеры, определенным образом ориентированный в теле Земли и принимаемый для обработки геодезических измерений в данной стране.

Эллипсоид Красовского имеет параметры:

а= 6378245 м, в= 6356863 м, α =

Этот эллипсоид является наиболее подходящим к телу Земли в пределах России, называется референц-эллипсоидом.

4. Понятие о плане, карте, профиле. Номенклатура топокарт.

План – уменьшенное и подобное изображение на плоскости (на бумаге) горизонтальныхпроекций небольших участков местности (мах. 20х20км.) учета кривизны Земли.

Карта – уменьшенное и построенное по определенным математическим законам уменьшенное изображение на плоскости значительных частей земной поверхности, размеры которых не позволяют пренебречь кривизной Земли..Карта, с изображением ситуации и рельефа называется топографической.

Топокарты имеют многоцелевое назначение, поэтому на них показывают все элементы местности. Профили местности представляют собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного или заданного направления.

Масштабы:

-Числовой 1:1000 1 см. планы или карты – 1000 см. на местности 1 см. – 10 м.

-Линейный

-Поперечный

Для удобства пользования картой размер одного листа принят близким к квадрату со стороной 40-50 см. Границами листа карты служат меридианы и параллели, широты и долготы которых выбраны так, чтобы обеспечивался указанный размер листа.

Система обозначения листов карт называется номенклатурой.

Деление карт на отдельные листы меридианами и параллелями называется разграфкой.Для топопланов участков местности площадью менее 20 кв. км применяется квадратная разграфка.В основу разграфки планов положен лист масштаба 1:5000, обозначенный условной арабской цифрой, но не в скобках.В пределах этого листа расположены 4 листа плана масштаба 1:2000 с обозначением листов заглавными буквами русского алфавита (А,Б,В,Г). Каждый лист плана масштаба 1:2000 содержит 4 листа плана масштаба 1:1000 с обозначением их римскими цифрами (1, 11, 111, 1V) или 16 листов плана масштаба 1:500 с обозначением их арабскими цифрами (1,2,3,...16).