Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость силы от расстоянияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
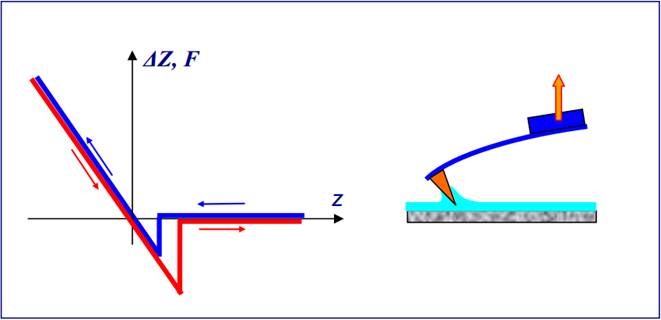
С помощью атомно-силового микроскопа можно изучать особенности локального силового взаимодействия зонда с поверхностью и на основании результатов данных исследований судить о свойствах поверхности различных образцов. С этой целью снимаются так называемые кривые подвода зонда к поверхности и кривые отвода. Фактически это зависимости величины изгиба кантилевера ∆Z (а следовательно, и силы взаимодействия зонда с поверхностью) от координаты z при сближении зондового датчика и образца. Аналогичные измерения проводятся при удалении зонда от поверхности. Характерный вид зависимости ∆Z = f(z) изображен на рисунке 12.
Рисунок 12 – Схематическое изображение зависимости изгиба кантилевера (силы взаимодействия зонда с поверхностью) от расстояния Z между зондовым датчиком и поверхностью образца. Прямой и обратный ход показаны разным цветом При приближении к поверхности образца зонд попадает в область действия сил притяжения. Это вызывает изгиб кантилевера в направлении к поверхности (рисунок 12, вставка (а)). В этой области может наблюдаться явление скачка зонда к поверхности, обусловленное наличием большого градиента сил притяжения вблизи поверхности образца. Для потенциала типа Леннарда-Джонса область больших градиентов силы притяжения составляет Z* ~ 1 нм. На рисунке 13 схематически показаны зависимости силы Леннарда-Джонса и ее производной от расстояния между зондом и поверхностью.
Рисунок 13 – Схематическое изображение зависимости силы (а) и её производной (б) по координате Z от расстояния зонд-поверхность
Для наблюдения эффекта скачка зонда к поверхности необходимо, чтобы жесткость выбранного кантилевера была меньше, чем максимум производной силы по координате z. Поясним данный эффект на примере модели малых колебаний консоли. Действительно, уравнение движения упругого кантилевера вблизи поверхности выглядит следующим образом:
где
При переходе к новым переменным,
Это уравнение осциллятора с частотой, зависящей от расстояния При дальнейшем сближении зондового датчика и образца зонд начинает испытывать отталкивание со стороны поверхности, и кантилевер изгибается в другую сторону (рисунок 12, вставка (б)). Наклон кривой ∆Z = f(z)на этом участке определяется упругими свойствами образца и кантилевера. Если взаимодействие зонда и образца абсолютно упругое, то зависимость изгиба кантилевера от расстояния АСМ датчик - поверхность, регистрируемая на обратном ходе, совпадает с зависимостью, получаемой на прямом ходе (рисунок 12). Для мягких (пластичных) образцов, таких как пленки органических материалов, биологические структуры и др., а также для образцов, на поверхности которых находятся адсорбированные слои различных материалов, кривые ∆Z = f(z) имеют более сложный характер. В этом случае на вид зависимости существенное влияние оказывают эффекты капиллярности и пластичности. В качестве примера, на рисунке 14 показаны кривые подвода-отвода для образца, содержащего на поверхности слой жидкости. На данных зависимостях наблюдается гистерезис, связанный с эффектами капиллярности. При подводе зондового датчика к образцу происходит смачивание зонда жидкостью, содержащейся на поверхности образца. При этом на границе контакта зонда с жидкостью формируется мениск. На зонд, погруженный в жидкость, действует дополнительная сила поверхностного натяжения. Это приводит к тому, что при отводе зондового датчика точка отрыва кантилевера от поверхности такого образца смещается в область больших Z.
Рисунок 14 - Схематическое изображение зависимости изгиба кантилевера от расстояния z между зондовым датчиком и образцом, содержащим на поверхности адсорбированный слой жидкости.
Таким образом, по виду зависимостей ∆Z = f(z) можно судить о характере взаимодействия зонда с поверхностью, исследовать локальную жесткость в различных точках образца, изучать распределение сил адгезии на поверхности образцов.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.170 (0.007 с.) |



 , (8)
, (8) - смещение кантилевера из равновесия,
- смещение кантилевера из равновесия,  - жёсткость кантилевера,
- жёсткость кантилевера,  - его масса,
- его масса,  - сила взаимодействия зонда с поверхностью,
- сила взаимодействия зонда с поверхностью, 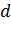 - расстояние между положением равновесия кантилевера и поверхностью. Линеаризуя данное уравнение, получаем:
- расстояние между положением равновесия кантилевера и поверхностью. Линеаризуя данное уравнение, получаем: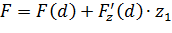 (9)
(9) (10)
(10) , уравнение движения приобретает следующий вид:
, уравнение движения приобретает следующий вид:
 . (11)
. (11)