
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконтактный режим колебаний кантилевера асмСодержание книги
Поиск на нашем сайте
(24)
(25)
(26)
(27)
(28) Производя вычисления, аналогичные вычислениям, проведенным для свободного кантилевера, получаем амплитудно-частотную характеристику системы:
(29)
(30)
(31) Следовательно, дополнительный сдвиг АЧХ равен
(32)
Рисунок 18 - Изменение АЧХ и ФЧХ кантилевера под действием градиента силы
(33)
(34)
(35) Он определяется производной z-компоненты силы по координате z. Данное обстоятельство используется для получения фазового контраста в АСМ исследованиях поверхности.
12 "Полуконтактный" режим колебаний кантилевера АСМ
Рисунок 19 - Выбор рабочей точки при "полуконтактном" режиме колебаний кантилевера
Регистрация изменения амплитуды и фазы колебаний кантилевера в бесконтактном режиме требует высокой чувствительности и устойчивости работы обратной связи. На практике чаще используется так называемый "полуконтактный" режим колебаний кантилевера (иногда его называют прерывисто-контактный, а в иностранной литературе - "intermittent contact" или "tapping mode" режимы). При работе в этом режиме возбуждаются вынужденные колебания кантилевера вблизи резонанса с амплитудой порядка 10 – 100 нм. Кантилевер подводится к поверхности так, чтобы в нижнем полупериоде колебаний происходило касание поверхности образца (это соответствует области отталкивания на графике зависимости силы от расстояния (рисунке 19)).
(36)
(37) Теория "полуконтактного" режима значительно сложнее теории бесконтактного режима, поскольку в этом случае уравнение, описывающее движение кантилевера, существенно нелинейно. Сила FPS = (z(t)) теперь не может быть разложена в ряд по малым z. Однако характерные особенности данного режима сходны с особенностями бесконтактного режима - амплитуда и фаза колебаний кантилевера зависят от степени взаимодействия поверхности и зонда в нижней точке колебаний кантилевера. Поскольку в нижней точке колебаний зонд механически взаимодействует с поверхностью, то на изменение амплитуды и фазы колебаний кантилевера в этом режиме существенное влияние оказывает локальная жесткость поверхности образцов. Сдвиг по фазе между колебаниями возбуждающего пьезоэлектрического вибратора и установившимися колебаниями кантилевера можно оценить, если рассмотреть процесс диссипации энергии при взаимодействии зонда с образцом. При установившихся колебаниях энергия, приходящая в систему, в точности равна энергии, рассеиваемой системой. Энергия, поступающая в систему от пьезовибратора за период колебаний:
(38)
(39)
(40)
(41) Предполагая, что установившиеся колебания кантилевера имеют вид
(42)
Отсюда для фазового сдвига получается следующее выражение:
Таким образом, фазовый сдвиг колебаний кантилевера в "полуконтактном" режиме определяется энергией диссипативного взаимодействия зонда с поверхностью образца. Формирование АСМ изображения поверхности в режиме колебаний кантилевера происходит следующим образом. С помощью пьезовибратора возбуждаются колебания кантилевера на частоте ω (близкой к резонансной частоте кантилевера) с амплитудой Аω. При сканировании система обратной связи АСМ поддерживает постоянной амплитуду колебаний кантилевера на уровне A0, задаваемом оператором (A0 < Аω). Напряжение в петле обратной связи (на z-электроде сканера) записывается в память компьютера в качестве АСМ изображения рельефа поверхности. Одновременно при сканировании образца в каждой точке регистрируется изменение фазы колебаний кантилевера, которое записывается в виде распределения фазового контраста.
Заключение:
Новая экспериментальная методика всегда позволяет увидеть и узнать то, что ранее было неизвестно. АСМ можно использовать для определения типа атома в кристаллической решётке. С помощью атомно-силового микроскопа удается наблюдать многие события, разыгрывающиеся на поверхности растущего кристалла (особенно кристалла белка), но, к сожалению, не все. Острие иглы кривизной 5 нм может различить периодическую структуру молекул на порядок меньшего размера, но не может различить адсорбированные поверхностью отдельные молекулы такого размера. Пока в растворе удается увидеть элементарные акты при соединения строительных единиц к кристаллам белков, но не к кристаллам неорганических соединений. В последнем случае неизвестно, что присоединяется к изломам, что является строительной единицей — ионы, молекулы или их группы. Это сдерживает развитие теории и не позволяет предсказать влияние различных факторов на кинетику кристаллизации. Нет также способа узнать, что происходит в приповерхностном слое раствора. Находящиеся в растворе ионы, молекулы и их комплексы окружены гидратными оболочками, непонятно где, как и в какой момент происходит освобождение от них. Сейчас можно только гадать, какой именно прибор позволит разобраться в этом. Перспективным направлением считается совмещение сканирующих зондовых микроскопов с другими традиционными и современными методами исследованиями, а также создание принципиально новых приборов. Например, совмещение СЗМ с оптическими микроскопами (традиционными и конфокальными микроскопами), электронными микроскопами, спектрометрами (например, спектрометрами комбинационного (рамановского) рассеяния и флуоресцентными), ультрамикротомами
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.006 с.) |

 В бесконтактном режиме кантилевер совершает вынужденные колебания с малой амплитудой порядка 1 нм. При приближении зонда к поверхности на катилевер начинает действовать дополнительная сила со стороны образца FPS. При ван-дер-ваальсовом взаимодействии это соответствует области расстояний между зондом и образцом, где действует сила притяжения. Если зонд АСМ находится на расстоянии z0 от поверхности, то для малых колебаний можно записать:
В бесконтактном режиме кантилевер совершает вынужденные колебания с малой амплитудой порядка 1 нм. При приближении зонда к поверхности на катилевер начинает действовать дополнительная сила со стороны образца FPS. При ван-дер-ваальсовом взаимодействии это соответствует области расстояний между зондом и образцом, где действует сила притяжения. Если зонд АСМ находится на расстоянии z0 от поверхности, то для малых колебаний можно записать: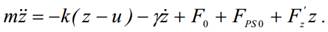 Это приводит к тому, что в правой части уравнения, описывающего колебания в такой системе, появляются дополнительные слагаемые:
Это приводит к тому, что в правой части уравнения, описывающего колебания в такой системе, появляются дополнительные слагаемые: Вводя новые переменные:
Вводя новые переменные:  , приходим к уравнению:
, приходим к уравнению: Т.е. наличие градиента сил приводит к изменению эффективной жесткости системы:
Т.е. наличие градиента сил приводит к изменению эффективной жесткости системы: После стандартных преобразований уравнение записывается в следующем виде:
После стандартных преобразований уравнение записывается в следующем виде:
 И, соответственно, ФЧХ
И, соответственно, ФЧХ Таким образом, наличие градиента силы взаимодействия зонда с поверхностью образца приводит к дополнительному сдвигу АЧХ и ФЧХ системы. Резонансная частота в присутствии внешней силы ωrf может быть представлена в виде
Таким образом, наличие градиента силы взаимодействия зонда с поверхностью образца приводит к дополнительному сдвигу АЧХ и ФЧХ системы. Резонансная частота в присутствии внешней силы ωrf может быть представлена в виде

 Из выражения (30) также следует, что наличие градиента силы приводит к сдвигу ФЧХ, так что точка ее перегиба ω* находится на частоте
Из выражения (30) также следует, что наличие градиента силы приводит к сдвигу ФЧХ, так что точка ее перегиба ω* находится на частоте Пусть кантилевер вдали от поверхности совершает вынужденные колебания на частоте ω0, тогда сдвиг фазы его колебаний составляет π/2. При сближении с поверхностью фаза колебаний (считаем Fz’ < k) станет равной
Пусть кантилевер вдали от поверхности совершает вынужденные колебания на частоте ω0, тогда сдвиг фазы его колебаний составляет π/2. При сближении с поверхностью фаза колебаний (считаем Fz’ < k) станет равной Следовательно, дополнительный сдвиг фазы при наличии градиента силы будет равен:
Следовательно, дополнительный сдвиг фазы при наличии градиента силы будет равен:
 При сканировании образца регистрируется изменение амплитуды и фазы колебаний кантилевера. Взаимодействие кантилевера с поверхностью в "полуконтактном" режиме состоит из ван-дер-ваальсового взаимодействия, к которому в момент касания добавляется упругая сила, действующая на кантилевер со стороны поверхности. Если обозначить через z0 расстояние между положением равновесия колеблющегося кантилевера и поверхностью, а через FPS = (z(t)) - комбинированную силу, то уравнение движения кантилевера можно записать в следующем виде:
При сканировании образца регистрируется изменение амплитуды и фазы колебаний кантилевера. Взаимодействие кантилевера с поверхностью в "полуконтактном" режиме состоит из ван-дер-ваальсового взаимодействия, к которому в момент касания добавляется упругая сила, действующая на кантилевер со стороны поверхности. Если обозначить через z0 расстояние между положением равновесия колеблющегося кантилевера и поверхностью, а через FPS = (z(t)) - комбинированную силу, то уравнение движения кантилевера можно записать в следующем виде: где координата z отсчитывается от поверхности. Заметим, что "полуконтактный" режим реализуется только тогда, когда расстояние z0 меньше амплитуды колебаний кантилевера:
где координата z отсчитывается от поверхности. Заметим, что "полуконтактный" режим реализуется только тогда, когда расстояние z0 меньше амплитуды колебаний кантилевера:
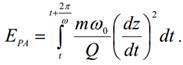 Она расходуется на восполнение потерь при взаимодействии кантилевера с атмосферой и образцом. Энергию EPA, рассеиваемую в атмосферу за период, можно вычислить следующим образом:
Она расходуется на восполнение потерь при взаимодействии кантилевера с атмосферой и образцом. Энергию EPA, рассеиваемую в атмосферу за период, можно вычислить следующим образом: Энергия EPS, идущая на восполнение потерь при диссипативном взаимодействии зонда с образцом, равна:
Энергия EPS, идущая на восполнение потерь при диссипативном взаимодействии зонда с образцом, равна: Из условия баланса следует:
Из условия баланса следует: z = A⋅cos(ωt + φ), получаем:
z = A⋅cos(ωt + φ), получаем: (43)
(43)


