
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стійкість укосів земляних гребельСодержание книги
Поиск на нашем сайте
Грунтові греблі – це досить великі грунтові масиви, які мають значну вагу, тому зсув таких масивів під дією горизонтальних сил практично неможливий. Але при деяких умовах експлуатації втрачають свою стійкість укоси, в результаті чого проходить сповзання частини масиву в межах тіла греблі (рис. 4.13 а), при цьому може бути захоплена і частина грунту основи (рис. 4.13 б). Стійкість укосу повинна бути забезпечена при всіх можливих схемах роботи споруди. Розрахунки стійкості укосів проводяться при заданих фізико-механічних характеристиках грунту тіла греблі і основи, відомих геометричних розмірах поперечного профілю і побудованій кривій депресії. В результаті розрахунків визначається мінімальне значення коефіцієнта стійкості укосів, яке має бути більшим за нормативне значення для даного класу споруди при тому чи іншому поєднанні навантажень.
Рис. 4.13. Види сповзання укосів: а – в межах тіла греблі; б – з частиною основи
Методів, на основі яких можна визначити стійкість укосів, є досить багато. Терцагі, Крей, О.О. Ничипорович, Р.Р. Чугаєв запропонували досить оригінальні методи, які широко використовуються в практиці проектування земляних споруд. Найбільше поширення отримав метод розрахунку стійкості по круглоциліндричних поверхнях ковзання, в якому приймається, що сповзання частини ґрунтового масиву проходить по радіальній кривій відносно деякого центру ковзання (точка О 1) (рис. 4.14). Стійкість укосу повинна бути перевірена по всіх можливих поверхнях ковзання із знаходженням найбільш небезпечної призми зрушення, яка характеризується мінімальним відношенням узагальнених граничних реактивних сил опору до активних сил зсуву. При пошуках небезпечної поверхні ковзання може бути використана залежність для коефіцієнта стійкості
де R – узагальнене розрахункове значення сил (або їх моментів) граничного опору зсуву по поверхні, що розглядається; F – рівнодіюча активних сил (або моментів цих сил) відносно центра поверхні ковзання. Вибір центра кривої ковзання може бути проведений довільно. Але при розрахунках стійкості укосів для знаходження центрів кривих ковзання з мінімальним значенням коефіцієнта стійкості існує значна кількість розрахункових способів. Для визначення критичного центра радіуса кривої ковзання В.В. Арістовський рекомендує таку побудову. Від середини укосу (точка а, рис, 4.14 а), або якщо укіс має ломане окреслення, то знаходиться його середнє значення закладання, проводиться вертикаль ас. Далі із тієї ж точки а під кутом 85° до укосу (або його середнього окреслення) проводиться лінія аd. Із точок А і В, як з центрів, проводяться криві радіусом R 1, які перетнуть промені ас і аd в точках в 1 і е 1, а самі перетнуться в точці О. Значення радіуса R 1 визначається за формулою
де Rн – нижнє і R в – верхнє значення радіусів поверхні зсуву. Орієнтовні значення Rн і R в в залежності від коефіцієнта закладання укосу наведені в таблиці 4.3.
Таблиця 4.3. Орієнтовні значення Rн і R в в частинах від висоти греблі Нгр
Рис. 4.14. Схема до розрахунку стійкості низового укосу: I – грунт тіла греблі природної вологості; ІІ – грунт тіла греблі, зважений у воді; ІІІ – грунт основи, зважений у воді
З точки а, як із центра, проводиться дуга ве радіусом R 2 = а О/2. Многокутник вв 1 Ое 1 е є зоною пробних центрів кривих ковзання. В межах цієї зони буде розташований критичний центр заданого радіуса кривої ковзання. При малих значеннях питомої зчепності грунту греблі с критичний центр розташовується близько або в самій вершині О зони пробних центрів. Із збільшенням значення с критичний центр відходить від вершини О. В.В. Арістовський встановив, що пробні центри найбільш небезпечних кривих ковзання розташовуються близько до лінії Ов, і ця лінія вибирається як лінія пробних центрів. Задавшись на лінії пробних центрів довільною точкою О 1, з неї, як з центру, проводиться дуга кола радіусом R, яка повинна відтинати приблизно половину гребеня зверху і частину основи внизу. В зв'язку з тим, що в більшості випадків грунти призми зрушення мають різні характеристики, то використати формулу (4.40) для всього масиву дещо складно. Враховуючи це, застосовується штучний спосіб, який базується на тому, що розглядається стійкість виділених з масиву відсіків шириною вв,які утворені вертикальними площинами (рис. 4.14 б). Ця ширина може бути взята довільно, але частіше всього її вибирають рівною 0,1 R (що спрощує визначення тригонометричних функцій, які входять у формулу), крім останніх (крайніх), ширини яких будуть менші.
На тіло зрушення, що обмежене кривою ковзання і поверхнею укосу, будуть діяти такі сили: власна вага грунту в межах контуру, сила тертя і сила зчеплення, які прикладені по поверхні ковзання (рис. 4.14 а) та гідродинамічна сила фільтраційного потоку, що враховується як об'ємна в межах контуру СDFBKC. Всі розрахунки проводяться на 1 погонний метр ширини греблі. Відсіки по висоті мають різні грунти, а, відповідно, і різну питому вагу, тому при визначенні власної ваги відсіку знаходять приведену висоту відсіку hпв з постійним значенням питомої ваги грунту ρгрg. Приведена висота визначається для грунту тіла греблі природної вологості ρгр, використовуючи формулу
де hпр – висота частини відсіку грунту, що знаходиться в стані природної вологості; h 1, h 2... hп – частини висот відсіку, що відповідають різним грунтам тіла греблі і основи, насичені водою; ρгр – щільність грунту тіла греблі природної вологості; ρн', ρн"...ρпн –щільності грунтів насичених водою. Значення щільності грунту, насиченого водою, визначається за залежністю ρн = (ρs – ρ)/(1 + п),де ρs – щільність твердих часток грунту; п - коефіцієнт пористості. Таким чином, сила власної ваги окремого відсіку буде G = вв hnв ρгр g. Ця сила повинна бути прикладена в центрі тяжіння відсіку, але вона переноситься по лінії її дії на криву ковзання і розкладається на дві складові: нормальну N = Gcos α 2= вв hnв ρгр gcos α 2 і дотичну Т2 = Gsin α 2 = вв hnв ρгр gsin α 2,де α 2 – кут між вертикаллю і вектором нормальної сили (рис. 4.14 б). Нормальна складова власної ваги N викликає появу сили тертя Т=Ntgφ = Gcos α 2tgφ,де - φ кут внутрішнього тертя грунту укосу. Значення сили зчеплення Т1 = сl, де l – довжина підошви відсіку (рис. 4.14 б). Коефіцієнт запасу на стійкість довільно вибраного відсіку без врахування гідродинамічної сили у відповідності з формулою (4.40) буде
де R – радіус дуги ковзання. Підставивши відповідні значення сил Т, Т 1 і Т 2 у формулу (4.43), отримаємо
Для всього масиву зрушення коефіцієнт стійкості ks визначається як співвідношення суми моментів сил по окремих відсіках і формула (4.44) буде мати вигляд
Цей вираз для ks є основним для всіх методів розрахунку з розбивкою масиву зрушення на окремі відсіки при відсутності інших зовнішніх сил. При наявності в тілі греблі фільтраційного потоку для обчислення значення гідродинамічної сили в межах масиву зрушення поступають таким чином. Розглядають один з відсіків призми зрушення (рис. 4.14 б). Різниця гідростатичних тисків на вертикальних гранях відсіку буде дорівнювати ρgввti,де і – середній градієнт напору потоку ґрунтових вод; t – середня глибина потоку від підошви відсіку до кривої депресії. Сумуючи ці різниці по всій зоні фільтраційного потоку від кривої зсуву до лінії депресії, отримуємо гідродинамічну силу, яка дорівнює Ф = ρgΣввtiіср = ρgАіср, де А – площа області фільтраційного потоку СDМС; іср – середній градієнт напору фільтраційного потоку в області А (середній уклон прямої СD). Сила прикладена в центрі тяжіння площі А і направлена паралельно середньому уклону. Відстань від центру тяжіння площі А до точки О 1, яка дорівнює r,є плечем цієї сили.
В зоні DЕВКМD,де напрям руху потоку близький до вертикального, значення гідродинамічної сили досить незначне і ним можна знехтувати. Таким чином, враховуючи значення гідродинамічної сили і її момент, що дорівнює Фr, отримуємо вираз для коефіцієнта стійкості
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 731; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.45.22 (0.011 с.) |



 , (4.40)
, (4.40)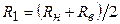 , (4.41)
, (4.41)
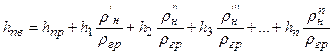 , (4.42)
, (4.42) , (4.43)
, (4.43) . (4.44)
. (4.44) . (4.45)
. (4.45)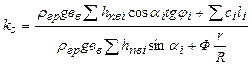 . (4.46)
. (4.46)


