
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фільтрація через греблю з ядром, екраном, екраном іСодержание книги
Поиск на нашем сайте
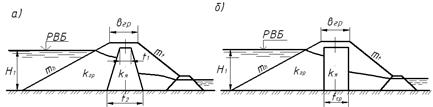
Понуром Для зменшення фільтраційної витрати і швидкості фільтраційного потоку, а також для зниженнякривої депресії, в середній частині профілю в земляних греблях влаштовується ядро змаловодопроникних грунтів. Коефіцієнт фільтрації ядра кя значно менший за коефіцієнт фільтраціїгрунту тіла греблі кгр і тому, навіть при незначній товщині ядра, втрати напору в його межах досягають значних величин і крива депресії різко знижується (рис. 4.7).
Рис. 4.7. Схеми до фільтраційного розрахунку греблі з ядром: а – задана; б – приведена
Використавши рівняння Дюп'юї, М. М. Павловський отримав вираз для визначення фільтраційної витрати через ядро. При цьому, для спрощення розрахунків, трапецієвидний профіль ядра замінено прямокутним з такою ж площею поперечного перерізу і середньою товщиною tcp = (t 1 +t 2 )/ 2 (рис.4.7 б). Фільтраційні витрати в межах верхової і низової призм визначаються таким же чином, як і для однорідної греблі. В результаті отримано систему з 6 рівнянь, але спосіб визначення невідомих в цій системі досить складний. Замість громіздкого розв'язку системи рівнянь М. М. Павловський запропонував більш простий метод розрахунку, який названо віртуальним. Його суть полягає в тому, що земляна гребля з ядром замінюється відповідною еквівалентною однорідною греблею. Для того, щоб зрозуміти суть методу, розглянемо два ґрунтових потоки, які проходять в однорідних грунтах з однаковою питомою витратою. Грунти мають різні коефіцієнти фільтрації к 1 і к 2, але падіння кривої депресії в, обох випадках однакове і складає h 1 - h 2 (рис. 4.8 а, б). Рівняння кривої депресії для обох ґрунтових потоків може бути записане як для середньої частинки однорідної греблі. Для першого ґрунтового потоку
Рис. 4.8. Схеми до розрахунку фільтрації через греблю з ядром віртуальним методом
Відповідно рівняння кривої депресії для другого потоку
Прирівнявши ліві частини рівнянь (4.26) і (4.27), та скоротивши на 2, отримуємо
Аналізуючи залежність (4.28), приходимо до висновку, що при однакових питомих витратах і однакових граничних глибинах довжини ділянок розглянутих потоків прямо пропорційні коефіцієнтам фільтрації. Отже, першу фільтраційну схему з коефіцієнтом фільтрації к 1 можна замінити еквівалентною (у відношенні втрат напору) другою фільтраційною схемою з коефіцієнтом фільтрації к2 з такою умовою, щоб довжина ділянки потоку в другій розрахунковій схемі задовольняла умові (4.28), звідки довжина другої еквівалентної ділянки буде
де σ = к 2/ к 1. На основі цього греблю з ядром (рис. 4.7 б) можна замінити еквівалентною однорідною греблею (рис. 4.8 в). Якщо коефіцієнт фільтрації ядра кя, тіла греблі кгр,а співвідношення кгр/кя = σ,то приведена (віртуальна) ширина ядра буде tv = σtср. Приведена ширина гребеня bv = 2 с + tv або bv = bгр + tср (σ - 1). Далі, за залежністю (4.12), як для однорідної греблі, визначаються координати кривої депресії. Якщо осі координат розташовані, як показано на рис. 4.8 в, то ординату точки Е кривої депресії отримаємо при х = с,а приймаючи значення х = с + tv,будемо мати ординату точки D – точки виходу кривої депресії з ядра. Для побудови гілки DС кривої депресії, яка розташована справа від перерізу 2-2, значенням х необхідно задатися в межах с + tv ≤ x ≤ Sv. Очевидно, при х = Sv отримаємо ординату точки С - виходу кривої депресії на низовому укосі. Для того, щоб отримати дійсне положення кривої депресії в греблі з ядром (рис. 4.7), зсуваємо верхову і низову частини греблі так, щоб відстань між перерізами 1-1 і 2-2 стала дорівнювати tср (рис.4.7 в), а гілки АЕ і DС побудованої кривої депресії залишилися незмінними (рис. 4.7 а). Гребля з екраном. У відповідності із збільшенням глибини води у верхньому б'єфі екрани влаштовуються з поступовим потовщенням до нижньої частини укосу греблі (рис. 4.9), але для спрощення фільтраційного розрахунку товщину екрана приймають середньою, що визначається за залежністю
Рис. 4.9. Схеми до фільтраційного розрахунку греблі з екраном: а – задана; б – приведена
де t 1 – товщина екрана на рівні води верхнього б'єфа нормально до укосу; t 2 – товщина екрана біля підошви греблі. М. М. Павловський, розглядаючи рух фільтраційного потоку через екран в двох зонах: через верхню частину екрана (вище кривої депресії) і через нижню частину екрана (нижче кривої депресії), для визначення повної фільтраційної витрати через екран отримав рівняння
де Н 1 – глибина води перед греблею; h3 – глибина фільтраційного потоку в тілі греблі безпосередньо за екраном; α – кут нахилу екрана до основи греблі; z0 = tcpcosα. За екраном рух фільтраційного потоку проходить так, як і в однорідній греблі з напором h3 (замість Н 1), отже для визначення фільтраційної витрати і побудови кривої депресії можна скористатися рівняннями для однорідної греблі. Грунтові греблі з екраном можна розраховувати як і з ядром –віртуальним методом. У відповідності з цим методом від похилої осі екрана W 1 W 1 відкладається по горизонталі вліво (рис. 4.10) віртуальна товщина
Рис. 4.10. Схема до розрахунку фільтрації через греблю з екраном
Для розрахунку дійсний профіль греблі з екраном (рис. 4.9) замінюється віртуальним профілем (рис. 4.10), який виконується з однорідного грунту з коефіцієнтом фільтрації кгр. Отриманий віртуальний профіль розраховується, як однорідна гребля. Низова гілка кривої депресії КL,побудованої для віртуального профілю, буде кривою депресії для дійсного профілю (в межах тіла греблі). Гребля з екраном і понуром. При розрахунках таких гребель втратами напору в захисному шарі нехтують. Екран і понур вважаються водонепроникними, коефіцієнт закладання укосу екрана визначають по середній лінії, а падіння напору по довжині понура вважається лінійним. Фільтраційна витрата q в межах понура і частини греблі на довжині mhhe (рис.4.11) визначається за залежністю
Рис. 4.11. Схема до фільтраційного розрахунку греблі з екраном і понуром
де к 0 – коефіцієнт фільтрації грунту основи; Т - товщина водопроникного шару основи; п - поправочний коефіцієнт, який вибирається з таблиці 4.1 із заміною в ній відношення L/Т на відношення Lпд / Т. Таблиця 4.1 Значення поправочного коефіцієнта п
Для іншої частини потоку в межах греблі та ж витрата визначається за залежністю
де кгр – коефіцієнт фільтрації тіла греблі. Для усталеного руху фільтраційного потоку праві частини рівнянь (4.33) і (4.34) можна прирівняти і тоді отримаємо розрахункове рівняння
з якого підбором визначається глибина фільтраційного потоку h е за екраном. Для цього при довільних значеннях h будуються криві для лівої і правої частин рівняння (4.35), а точка перетину їх дає дійсне значення h е. Подальший розрахунок зводиться до розрахунку однорідної греблі з напором, який дорівнює h е. Для побудови кривої депресії можна скористатися рівнянням
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.250.187 (0.01 с.) |

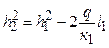 або
або  . (4.26)
. (4.26)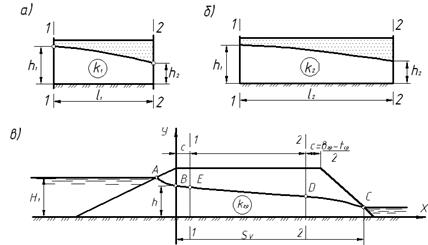
 . (4.27)
. (4.27)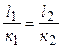 . (4.28)
. (4.28)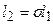 , (4.29)
, (4.29)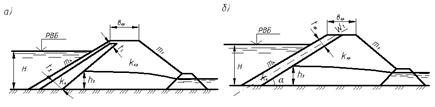
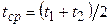 , (4.30)
, (4.30)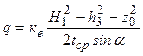 , (4.31)
, (4.31) . (4.32)
. (4.32)
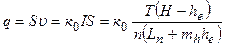 , (4.33)
, (4.33)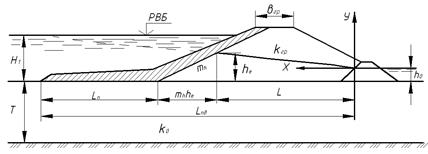
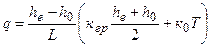 , (4.34)
, (4.34)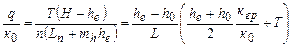 , (4.35)
, (4.35) . (4.36)
. (4.36)


