
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фільтрація через однорідну греблю на водонепроникній основіСодержание книги
Поиск на нашем сайте
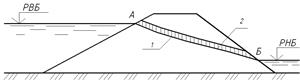
Під дією напору Н, який створює гребля, виникає рух фільтраційного потоку з верхнього б'єфа в нижній через тіло греблі і основу, якщо вона водопроникна. Рух ґрунтового потоку в тілі греблі буде безнапірним, тому що він обмежений зверху вільною поверхнею, на якій у всіх точках тиск дорівнює атмосферному. Вільна поверхня фільтраційного потоку називається поверхнею депресії, а лінія перетину цієї поверхні з вертикальною площиною — депресійною кривою або кривою депресії (рис. 4.1, крива АБ). Нижче поверхні депресії грунт насичений водою, а вище неї знаходиться зона капілярного підняття води. Висота капілярного підняття над кривою депресії залежить від складу грунту. Вище капілярної зони грунт знаходиться в умовах природної вологості, яка залежить від кліматичних умов району. Фільтрація води через грунтові греблі відіграє дуже важливу роль. Статистика показує, що більше 50% аварій ґрунтових гребель виникли як наслідок фільтраційних деформацій в тілі греблі. Тому при проектуванні ґрунтових гребель необхідно проводити фільтраційний розрахунок, в процесі якого визначаються: а) положення депресійної поверхні фільтраційного потоку в тілі греблі; б) фільтраційна витрата; в) напори (або градієнти фільтраційного напору) у відповідних частинах тіла греблі. Відомі методи розрахунків фільтрації можна розділити на експериментальні, гідромеханічні і гідравлічні. З експериментальних методів найбільшого поширення набув метод ЕГДА. Він використовується при складних геологічних умовах основ споруди або складній конструкції греблі, а також при необхідності вирішення планових і просторових задач.
Рис. 4.1. Схема фільтрації води через земляну греблю: 1 – крива депресії; 2 - капілярна зона
Найбільш поширеними є гідравлічні методи розрахунку, в яких розглядається усталений фільтраційний потік в умовах плоскої задачі. Гідравлічні розрахунки дозволяють визначати положення кривої депресії, вираховувати фільтраційну витрату, середні значення градієнтів і швидкостей фільтраційного потоку. Для розрахунків проектний профіль греблі зводиться до розрахункової схеми, в якій виключаються всі незначні деталі і не враховуються втрати напору в крупнозернистих привантаженнях, що укладені зверху малопроникних елементів. Рівні води в розрахункових схемах повинні відповідати їх фізично можливому поєднанню, при яких характеристики фільтраційного потоку будуть найменш сприятливими з точки зору міцності і стійкості греблі, а також втрат води на фільтрацію. У відповідності з загальним гідравлічним методом розрахунку фільтрації, який був розроблений М. М. Павловським, поперечний профіль греблі розбивається на три характерні частини: верховий клин, середню частину і низовий клин (рис. 4.2).
Верховий клин обмежений верховим укосом греблі і вертикальним перерізом 1-1, який проходить через верхню бровку гребеня греблі; середня частина – від перерізу 1-1 до перерізу 2-2, який проходить через точку С виходу кривої депресії на низовому укосі греблі; низовий клин, обмежений низовим укосом і перерізом 2-2. При цьому всі три частини складають одне гідравлічне ціле, тому що кожна з них пропускає одну і ту ж питому витрату q. Верховий клин. Лінія верхового укосу є лінією рівного напору, тому що в довільно взятій точці, яка лежить на цій лінії, напір буде дорівнювати Н.
Рис. 4.3. Розрахункова схема фільтрації через верховий клин Наприклад, в точці М (рис. 4.3 а), ордината якої над горизонтальною площиною порівняння (вісь х) дорівнює у і тиск в якій р, значення напору буде Н=р/ρg+у=const. Фільтраційні струминки при вході їх в межі верхового клину повинні бути розташовані нормально до верхового укосу, але при виведенні фільтраційного рівняння для верхового клину М. М. Павловський криволінійні струминки ас (рис. 4.3 б) замінює прямолінійними і горизонтальними dв. Струминки при цьому будуть більш видовженими і, тим самим, ніби зменшується пропускна спроможність верхового клину. Це обумовлюється тим, що струминки, які розташовані на більшій глибині (наприклад, струминка ef)близько підходять до водонепроникної основи і у відповідній частині верхового укосу (заштрихована на рис. 4.3 б зона D)має місце досить повільна фільтрація і тому зменшується пропускна спроможність верхового клину. Крім того, криволінійні фільтраційні струминки зустрічають більший опір на одиницю довжини, перетинаючи ущільнені горизонтальні шари тіла греблі. Тому, при виведенні фільтраційного рівняння для верхового клину, М. М. Павловський знайшов можливим криволінійні струминки замінити розрахунковими прямолінійними і горизонтальними. В такому випадку розрахункова схема фільтрації для верхового клину буде мати вигляд, який показано на рис. 4.3 а. При фільтрації в межах верхового клину виникають гідравлічні опори, на подолання яких втрачається деяка частина напору. Тому крива депресії в межах верхового клину знижується від початкової точки А з напором, що дорівнює Н, до точки В, яка розташовується на перерізі 1-1, де глибина фільтраційного потоку дорівнює h. Позначивши втрату напору в межах верхового клину через а, отримаємо а = Н - h. Довжина розрахункової струминки, що розташована під рівнем води верхнього б'єфа на глибині z, буде
де mh – коефіцієнт закладання верхового укосу; d – перевищення гребеня греблі над розрахунковим рівнем води. В межах верхового клина втрата напору складає а, відповідно градієнт напору
Швидкість фільтрації
де к – коефіцієнт фільтрації грунту тіла греблі. Якщо площа поперечного перерізу елементарної струминки ds = dz 1, то елементарна фільтраційна витрата цієї струминки буде
Інтегруючи це рівняння в межах від z = a до z = a+h, отримаємо повну фільтраційну витрату через тіло греблі на одиницю її довжини
або
З рис. 4.3 а видно, що а = Нгр - d - h; d+a = Нгр – h; d+a+h = Нгр. Підставивши ці значення в залежність 4.5, отримаємо фільтраційне рівняння для верхового клину
Середня частина. В середній частині греблі виникає нерівномірний, повільно змінний рух ґрунтового потоку і крива депресії в середній частині має вигляд кривої спаду. При цьому глибина фільтраційного потоку поступово зменшується від значення h до значення h 1. В кожному довільно вибраному перерізі середня швидкість υ = const, але в різних перерізах різна, тому що значення уклону dy/dx змінне (рис.4.4 б). В довільно вибраному перерізі А-А швидкість руху фільтраційного потоку дорівнює υ, для нерівномірного, повільно змінного руху вона визначається за формулою Дюп'юї
Виходячи з умови, що в довільно вибраному перерізі проходить постійна витрата, в умовах усталеного руху питома витрата буде
Рис. 4.4. Розрахункова схема фільтрації через середню частину
Підставивши значення υ в рівняння (4.8), отримуємо
Приведемо рівняння до зручного для інтегрування вигляду
і при його інтегруванні отримуємо
Постійна інтегрування С визначається із умови, що при х = 0 ордината у = h, так що з рівняння (4.9) отримуємо
При цьому значенні С рівняння (4.9) буде мати вигляд
Це і є рівняння кривої депресії для середньої частини греблі. За ним можна побудувати криву депресії, для чого, задаючись різними значеннями х, які знаходяться в межах від х = 0 до х = S, визначаються відповідні значення у. При х = S значення у = h 1 і рівняння (4.10) має вигляд
а остаточне фільтраційне рівняння для середньої частини буде
Низовий клин. Тут може бути два випадки: вода в нижньому б'єфі відсутня, h 0 = 0; наявність води в нижньому б'єфі, h 0 > 0. Випадок 1, h 0 = 0. Вибираємо, як і для верхового клину, елементарну горизонтальну розрахункову струминку товщиною dz. Довжина цієї струминки l = mtz,де z – заглиблення струминки під точкою виходу С кривої депресії на низовий укіс греблі (рис. 4.5). Втрата напору в даній струминці hв = z. Гідравлічний уклон струминки
Швидкість руху фільтраційного потоку
Елементарна фільтраційна витрата для струминки
Якщо позначити перевищення точки виходу кривої депресії С над дном нижнього б'єфа через а0, то повна фільтраційна витрата буде
Рівняння для низового клину має вигляд
Випадок 2, h 0 > 0. В низовому клині при наявності води в нижньому б'єфі фільтраційний потік має дві зони (рис. 4.6): верхня зона від точки С до рівня води в нижньому б'єфі, де фільтраційний потік виходить в атмосферу з витратою q 1, і нижня зона – від рівня води нижнього б'єфа до підошви греблі, де вихід фільтраційного потоку йде під рівень з витратою q 2. Загальна питома фільтраційна витрата через тіло греблі складає
Рис. 4.5. Розрахункова схема фільтрації через низовий клин при h 0 = 0
Фільтраційний потік, що проходить через низовий клин, повинен подолати гідравлічні опори і тому він повинен мати деякий надлишок енергії в порівнянні із значенням її у вихідному перерізі. Тому вважається, що вихідна точка С депресійної кривої розташовується вище рівня води в нижньому б'єфі на деяку величину а 0, тоді h 1 = а 0+ h 0. Витрата через верхню зону q 1для випадку h 0 = 0 визначається за залежністю
Розглянемо фільтрацію в нижній зоні (рис.4.6). Довжина елементарної струминки l = zmt; втрата напору а 0 = const; гідравлічний уклон
швидкість фільтрації
Елементарна питома витрата для струминки нижньої зони
Рис. 4.6. Розрахункова схема фільтрації через низовий клин при h 0>0
Витрата через нижню зону
Повну фільтраційну витрату через низовий клин отримаємо, сумуючи питомі фільтраційні витрати через верхню і нижню зони,
В трьох рівняннях (4.6), (4.12), (4.24), отриманих для трьох частин греблі, є чотири невідомі значення а 0, h, S, q. Для розв'язку системи рівнянь необхідне четверте рівняння, яке отримуємо з побудови (рис. 4.4)
Розв'язок системи фільтраційних рівнянь дає можливість визначити невідомі значення а 0, h, q.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.102.43 (0.007 с.) |

 Гідромеханічні методи розрахунків, які базуються на розв'язку рівняння Лапласа при заданих граничних умовах, дають можливість визначити параметри потоку в довільно вибраній точці досить точно, але ці розв'язки надзвичайно складні, тому їх практичне використання досить обмежене.
Гідромеханічні методи розрахунків, які базуються на розв'язку рівняння Лапласа при заданих граничних умовах, дають можливість визначити параметри потоку в довільно вибраній точці досить точно, але ці розв'язки надзвичайно складні, тому їх практичне використання досить обмежене. Рис. 4.2. Розрахункова схема фільтрації
Рис. 4.2. Розрахункова схема фільтрації
 , (4.1)
, (4.1) . (4.2)
. (4.2) , (4.3)
, (4.3) . (4.4)
. (4.4)
 . (4.5)
. (4.5) . (4.6)
. (4.6) . (4.7)
. (4.7)
 . (4.8)
. (4.8) .
. ,
, . (4.9)
. (4.9) або
або  .
. . (4.10)
. (4.10) , (4.11)
, (4.11) . (4.12)
. (4.12) . (4.13)
. (4.13) . (4.14)
. (4.14) . (4.15)
. (4.15) . (4.16)
. (4.16) . (4.17)
. (4.17)
 . (4.18)
. (4.18)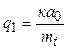 . (4.19)
. (4.19) ; (4.20)
; (4.20) (4.21)
(4.21) . (4.22)
. (4.22)
 (4.23)
(4.23) . (4.24)
. (4.24) . (4.25)
. (4.25)


