
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Где xmax и xmin соответственно наибольшее и наименьшее значения варьирующего признака.Содержание книги
Поиск на нашем сайте 2 Среднее линейное отклонение (d) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как взвешенной, так и невзвешенной: -- ∑ (x-x)f d = --------------- ∑ f 3 Дисперсия (σ2) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Дисперсия вычисляется по формулам простой невзвешенной и взвешенной: - 2 ∑(x-x)f δ =------------- ∑f 4 Среднее квадратическое отклонение (σ) представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней: δ =√δ 6 Коэффициент вариации: V=δ √ x*100 Эти показатели обычно выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Тема 5. Средние величины и показатели вариации. План: 1. Выборочный метод. Этапы выборочного метода. 2. Способы отбора единиц из генеральной совокупности. 3. Ошибки выборки. Ключевые слова: выборочная совокупность, ошибка выборки, генеральная совокупность, индивидуальный отбор, групповой отбор, комбинированный отбор. Выборочное наблюдение – такое не сплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные определенным образом. Цель (задача) выборочного наблюдения: по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов статистического наблюдения. Причины применения выборочного наблюдения: 1. экономия материальных, трудовых затрат и времени; 2. возможность более детально и подробно изучит отдельные единицы статистической совокупности и их группы. 3. некоторые специфические задачи можно решить только с применением выборочного наблюдения. 4. грамотное и хорошо организованное выборочное наблюдение дает высокую точность результатов. Генеральная совокупность – совокупность единиц, из которых производится отбор. Выборочная совокупность – совокупность отобранных для обследования единиц. В статистике принято различать параметры генеральной совокупности и выборочной совокупности.
Виды выборочного наблюдения По методу отбора: Повторное Попавшая в выборку единица после регистрации наблюдаемых признаков возвращаются в генеральную совокупность для участия в дальнейшей процедуре отбора. Объем генеральной совокупности остается неизменным, что обуславливает постоянное попадание в выборку какой-либо единицы. Бесповторное Попавшая в выборку единица не возвращается в совокупность, из которой происходит отбор. По способу отбора: Собственно-случайная заключается в отношении единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем проводить такую выборку, нужно убедиться, что все единицы генеральной совокупности имеют равные шансы попасть в выборку, т.е. в полном перечне единиц статистической совокупности отсутствуют пропуски или игнорирования отдельных единиц. Следует, также, четко установить границы генеральной совокупности. Технически сложившейся отбор осуществляется методом жеребьевки или с помощью таблицы случайных чисел. Механическая выборка (каждый 5 по списку) применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в распределении единиц. При проведении механической выборки устанавливается пропорция отбора, которая устанавливается соотношением генеральной совокупности и выборочной совокупности. Опасность ошибки при механической выборке может появляться вследствие: случайного совпадения выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Районированная выборка используется когда все единицы генеральной совокупности можно разбить на группы (районы, страны) по какому-либо признаку. Комбинированная выборка. Отбор единиц может быть произведен: 1. либо пропорционально объему группы 2. либо пропорционально внутригрупповой дифференциации признака 1. 2. Серийный отбор. Используется когда ЕСС объединены в небольшие группы (серии), например упаковка с готовой продукцией, студенческие группы. Сущность серийной выборки – серии отбираются собственно случайным, либо механическим способом, а затем осуществляется сплошное обследование внутри отобранной серии. Комбинированный отбор. Это комбинация рассмотренных выше способов отбора чаще применяется комбинация типичных и серийных серии, т.е. отбор серий из нескольких типических групп. Отбор моет быть еще многоступенчатым и одноступенчатым, многофразным и однофразным. Многоступенчатый отбор: из генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие, и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию. Многофразная выборка: предполагает сохранение одной и той же единицы отбора на всех этапах его проведения. При этом отобранные на каждой последующей стадии единицы отбора подвергаются обследованию, программа которого расширяется (Пример: студенты всего института, затем студенты каких-то факультетов).
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

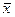
 , где n – объем выборочной совокупности, N – объем генеральной совокупности, ni – объем выборки i-группы, Ni – объем i выборки.
, где n – объем выборочной совокупности, N – объем генеральной совокупности, ni – объем выборки i-группы, Ni – объем i выборки. - этот способ является более точным, но в ходе проведения выборочного наблюдения очень трудно определить заранее о вариации. (до проявления наблюдения).
- этот способ является более точным, но в ходе проведения выборочного наблюдения очень трудно определить заранее о вариации. (до проявления наблюдения).


