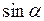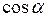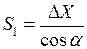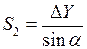Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вирівнювання ланцюга трикутників між сторонами тріангуляції вищого класу двогруповим корелатним способом
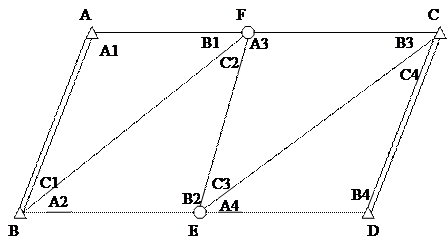
Розв’язання задачі вирівнювання ланцюга трикутників між сторонами тріангуляції вищого класу двогруповим корелатним способом виконуємо на конкретному прикладі (рис. 1, табл.1,
Рис. 1. Ланцюг трикутників тріангуляції
Вихідні дані та результати вимірів, виконаних на пунктах мережі, наведено у табл. 1, табл. 2.
Таблиця 1 Значення виміряних кутів у трикутниках тріангуляції
Для того, щоб зменшити число нормальних рівнянь, які виникають в мережі, тріангуляцію вирівнюємо не за напрямками, а за кутами. При вирівнюванні тріангуляції двогруповим корелатним способом умовні рівняння поділять на дві групи. В першу групу входять умовні рівняння даних фігур трикутників, які не перехрещуються, в другу – інші умовні рівняння фігур, горизонта, полюсні, дирекційних кутів, базисні та координат. Оскільки при вирівнюванні кутів умовні рівняння першої групи не мають спільних поправок (не залежать одине від одного), то розв’язання їх за методом найменших квадратів зводиться до розподілу нев’язки зі зворотнім знаком порівну у всі кути трикутника. Поправки кутів ν', отримані з розв’язання рівнянь першої групи називають первинними. Вторинні поправки ν'' в кути знаходяться після розв’язання рівнянь другої групи. Кінцева поправка в кут рівна сумі первинної та вторинної поправок. ν'і = ν'і + ν''і. (1.1)
Для визначення довжин сторін та дирекційних кутів необхідно розв’язати зворотню геодезичну задачу на площині, використовуючи формули:
де
Таблиця 2 Вихідні координати
1.1. Визначення числа умовних рівнянь Число умовних рівнянь у нашій мережі при вирівнюванні її по кутах визначаємо за формулами:
всього Sy = N*; фігур f = N – p – q; горизонту q = N + t – D; полюсних C = p – 2 n + 3; базисних і сторін t б = К б – 1; дирекцій них кутів і суми кутів tg= K g-1; tх, у = 2 (Кху – 1) абсцис і ординат, де N * – загальне число всіх виміряних в мережі кутів (N = 12), додатково виміряних сторін (Кs = 0) і азимутів (К N* = N + Кs + К Через (D = 18) визначено число напрямків, що утворюють усі виміряні в мережі кути; (n = 6) – число всіх пунктів в мережі; (К = 2) – число вирівнюваних пунктів; (р = 9) – число сторін в мережі. Кутові вимірювання виконані на (t = 6) пунктах; сила вихідних сторін (K s = 2); число вихідних дирекційних кутів (K g = 2). У мережі дві окремі групи вихідних пунктів К (х, у)= 2, тоді N *=8. Умовні рівняння фігур, віднесених до першої групи, будуть мати наступний вигляд:
Розв’язання умовних рівнянь показано в таблиці 3. Таблиця 3 Визначення поправок і довжин сторін трикутника
Закінчення табл. 3
Для обчислення довжин сторін трикутника використовуємо формули:
де а,в,с – сторони, А,В,С – виміряні кути. З оберненої геодезичної задачі визначаємо довжини сторін та їх дирекційні кути (табл. 4). Таблиця 4 Розв’язання оберненої геодезичної задачі
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.36.213 (0.011 с.) |
 ; (1.2)
; (1.2) , (1.3)
, (1.3)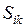 – відстань між пунктами; Хі Уі і Хк Ук – координати відповідно
– відстань між пунктами; Хі Уі і Хк Ук – координати відповідно  – дирекційний кут.
– дирекційний кут. = 0) разом взятих, тобто
= 0) разом взятих, тобто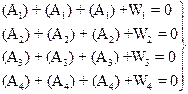 (1.5)
(1.5)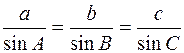 , (1.6)
, (1.6)