Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка информации на выпадающие точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Информация по показателям надежности, полученная в процессе испытаний или наблюдений в условиях рядовой эксплуатации, может содержать ошибочные точки, не соответствующие закону распределения случайной величины. Поэтому во время математической обработки информацию проверяют на выпадающие точки. Грубую проверку информации на выпадающие точки проводят по правилу. От полученного расчетным путем среднего значения показателя надежности Достоверности информации равны: Нижняя граница: Верхняя граница: Более точно информация на выпадающие точки проверяют по критерию Ирвина Фактическое значение критерия:
где ti и ti-1 - смежные точки информации. При Наименьшая точка информации:
Наибольшая точка информации
По таблице находим, что при повторности информации N=29 и Выполнение графического изображения опытного распределения показателя надежности
По данным статистического ряда могут быть построены гистограмма, полигон и кривая накопленных опытных вероятностей, которые дают наглядное представление об опытном распределении показателя надежности и позволяют решать ряд инженерных задач графическими способами. Для построения гистограммы по оси абсцисс откладывают в определенном масштабе показатель надежности
Рисунок 1 - Гистограмма распределения
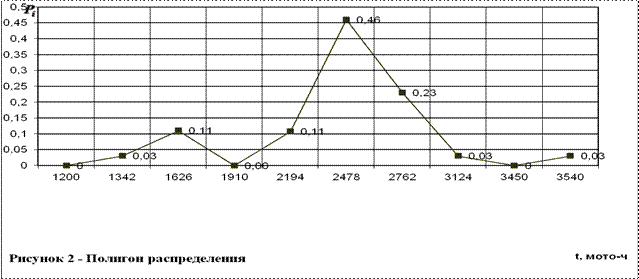
При построении полигона распределения (рисунок 2) по осям абсцисс и ординат откладывают те же значения, что и при построении гистограммы. Точки полигона распределения образуются пересечением ординаты, равной опытной вероятности интервала. Начальную и конечную точки полигона распределения приравнивают к абсциссам начала первого и конца последнего интервалов статистического ряда.
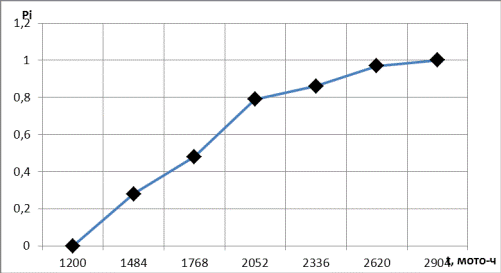
Для построения кривой накопленных опытных вероятностей по оси абсцисс откладывают в масштабе значение показателя надежности t, а по оси ординат - накопленную опытную вероятность Точки кривой накопленных опытных вероятностей образуются пересечением ординаты, равной сумме вероятностей
Рисунок 3 - Кривая накопленных опытных вероятностей надежность вариация интегральный дифференциальный
Определение коэффициента вариации
Коэффициент вариации представляет собой относительную безразмерную величину, характеризующую рассеивание показателя надежности. Коэффициент вариации:
где C - смещение начала рассеивания показателя надежности. При N < 25,
C =
При N > 25,
C=
C=1200 - V=
Выбор теоретического закона распределения для выравнивания опытной информации
Для выравнивания распределения показателей надежности сельскохозяйственной техники и ее элементов наиболее широко используется закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ). В первом приближении теоретический закон распределения выбирают по коэффициенту вариации: при V < 0,30, выбирают ЗНР, при V>0,50 - ЗРВ. Если значение коэффициента вариации находится в интервале 0,30….0,50, то выбирают тот закон распределения, который лучше совпадает с распределением опытной информации. В нашем примере V=0,54, поэтому предварительно принимаем ЗРВ.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.121 (0.008 с.) |

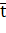 последовательно вычитают и прибавляют
последовательно вычитают и прибавляют 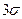 . Если крайние точки информации не выходят за пределы
. Если крайние точки информации не выходят за пределы 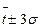 , то все точки информации считают действительными.
, то все точки информации считают действительными.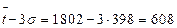 мото - ч
мото - ч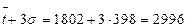 мото - ч
мото - ч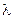 ,теоретическое значение которого
,теоретическое значение которого 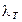 приведено в таблице 4.
приведено в таблице 4.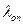 ≤
≤ 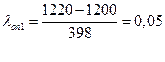
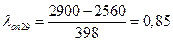
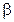 =0,95,
=0,95, 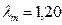 . Первую точку информации следует признать действительной, т.к. 0,05 <
. Первую точку информации следует признать действительной, т.к. 0,05 < 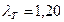 . Последнюю точку информации следует также признать действительной, т.к 0,85 <
. Последнюю точку информации следует также признать действительной, т.к 0,85 < 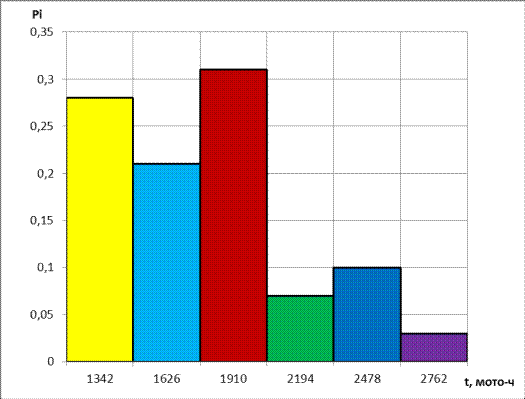
 .
.
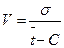 ,
,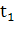 -
- 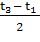 ;
;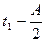
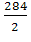 = 1058 мото-ч
= 1058 мото-ч