
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование для выравнивания распределения опытной информации закона нормального распределенияСодержание книги
Поиск на нашем сайте
Закон нормального распределения характеризуется дифференциальной (функцией плотностей вероятностей) и интегральной (функцией распределения) функциями. Отличительная особенность дифференциальной функции - симметричное рассеивание частных показателей надежности относительно среднего значения. Дифференциальная функция описывается уравнением
Если
Для определения дифференциальной функции через центрированную нормируемую дифференциальную функцию, используют уравнение:
f(t) =
где А - длина интервала,
tci - значение середины i-го интервала, t - среднее значение показателя надежности. Кроме того, следует пользоваться уравнением
Определим значения дифференциальной функции во всех интервалах статистического ряда
Интегральная функция (функция распределения) ЗНР определяем по уравнению:
При ti=0 и
Для определения интегральной функции через центрированную нормированную функцию, используют уравнение
где При этом используют уравнение
Рассчитаем значения интегральной функции для всех интервалов статистического ряда
Рассчитанные значения функций сводим в таблицу
Таблица - Значения дифференциальной и интегральной функций при ЗНР
На основании полученных дифференциальных и интегральных функций могут быть построены интегральные и дифференциальные кривые. Дифференциальная кривая заменяет полигон, интегральная кривая заменяет кривую накопленных опытных вероятностей. При построении дифференциальной кривой (рисунок 4) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значение дифференциальной функции. Точки пересечения образуются значением дифференциальной функции по оси ординат и значением середины i-го интервала по оси абсцисс.
При построении интегральной кривой (рисунок 5) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значением интегральной функции.
Определим число двигателей, потребующих ремонта в интервале наработки от 1700 - 2200 мото-ч. Решение: по дифференциальной функции:
по интегральной функции
Использование для выравнивания распределения опытной информации закона распределения Вейбулла
Дифференциальную функцию или функцию плотностей вероятностей ЗРВ описывают уравнение
где a,b - параметры ЗРВ. Параметр b определяют по таблице 3. Из таблицы выписывают параметр b коэффициенты kb и cb, предварительно посчитав коэффициент вариации. При V=0,54; b= 1,4; kb=0,91; Сb=0,66. Параметр a рассчитывают по одному из уравнений
Отсюда получаем
Дифференциальную функцию при ЗРВ определяют по таблице 5, используя уравнение
где А - длина интервала статистического ряда;
С - смещение начала рассеяния. Рассчитаем значения функции во всех интервалах статистического ряда
Интегральную функцию или функцию ЗРВ определяют по уравнению
Интегральная функция приведена в таблице 6. При этом используют уравнение
Определяем значения интегральной функции во всех интервалах статистического ряда
Рассчитанные значения функций сводим в таблицу
Таблица - Значения дифференциальной и интегральной функций при ЗРВ
На основании полученных значений f(t) и F(t) могут быть построен графики дифференциальных и интегральных функций закона распределения Вейбулла. При построении дифференциальной кривой (рисунок 6) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значение дифференциальной функции. Точки пересечения образуются значением дифференциальной функции по сои ординат и значением середины i-го интервала по оси абсцисс.
Рисунок 6. Дифференциальная кривая
При построении интегральной кривой (рисунок 7) по оси абсцисс откладывают значение показателя надежности в определенном масштабе, а по оси ординат значением интегральной функции.
Рисунок 7. Интегральная кривая
Определим число двигателей, требующих ремонта в интервале наработки от 1700 - 2200 мото-ч. Решение: по дифференциальной функции:
по интегральной функции
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.91.223 (0.006 с.) |


 =0 и
=0 и  , то получим уравнение для центрированной, нормированной дифференциальной функции.
, то получим уравнение для центрированной, нормированной дифференциальной функции.
 ,
, - среднее квадратичное отклонение,
- среднее квадратичное отклонение,






 - значение конца i-го интервала.
- значение конца i-го интервала.




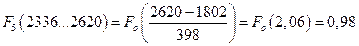



 .
. = 0,47∙29≈ 14 двиг.
= 0,47∙29≈ 14 двиг.
 ,
, или
или  ,
, мото-ч
мото-ч
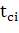 - середина интервала статистического ряда;
- середина интервала статистического ряда;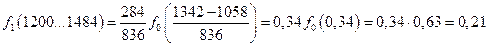















 .
.



