
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальные методы разукрупнения отдельных факторовСодержание книги
Поиск на нашем сайте
При построении модели детерминированного разложения анализируемого показателя по взаимодействующим факторам используется ряд формальных приемов разукрупнения отдельных факторов. Различают следующие приемы моделирования: 2.3.1. Метод удлинения факторной системы, он предусматривает удлинение числителя исходной модели путем расчленения одного или более факторов на составляющие элементы по схеме аддитивной зависимости и получения аддитивной модели с новым набором показателей – факторов.
2.3.2. Метод формального разложения факторной системы, он предусматривает удлинение знаменателя исходной модели путем расчленения одного и более факторов, не составляющих однородные элементы по схеме аддитивной зависимости.
2.3.3. Метод расширения факторной системы, он предусматривает преобразование исходной модели путем умножения числителя и знаменателя элементов исходной модели на один и более вводимый показатель фактора с последующим получением мультипликативной модели с новым набором факторов.
2.3.4. Стохастические методы экономического анализа Это методы корреляционного и регрессионного анализа. Они применяются тогда, когда невозможно заранее определить теоретические и строго определенный характер зависимости между факторными и результативным показателями. При проведении корреляционного анализа вводится предположение о характере зависимости между результативными и факторными признаками. Простейший вариант – это линейная зависимость результативного показателя «у» от фактора «х», тогда связь между ними определяется следующим уравнением. Ух = а0 + а1х Таким образом, первым этапом проведения корреляционного и регрессионного анализа является введение предположения о форме связи между результатом и факторами (кроме линейно, связь может быть квадратической, кубической, логарифмической, экспонинциальной). Связь между фактором и результатом будет вполне установлена если будут определены параметры уравнения регрессии а0 и а1. Они определяются в результате решения системы уравнений:
После расчета параметров а0 и а1, прежде чем использовать синтезированное уравнение регрессии анализа и прогнозирования, необходимо проверить тесноту связи между фактором и результатом и установить является ли она существенной.
При прямолинейной форме связи между фактором и результатом теснота связи определяется по формуле линейного коэффициента корреляции.
Рассчитанные значения коэффициента корреляции “r” интерпретируются в соответствии со шкалой:
Пример 4. Имеется следующая информация по однотипным предприятиям торговли о возрасте торгового оборудования и затратах на его ремонт. Необходимо построить модель зависимости расходов на ремонт от возраста оборудования.
Для определения параметров а0, а1 и коэффициента регрессии ‘r’ используется рабочая таблица следующей структуры:
Уравнение регрессии: у = а0 + а1*х у = -1,576 + 0,611 * х Проверим существенность связи между показателем у и х. Рассчитаем коэффициент корреляции.
Значение коэффициента корреляции свидетельствует о высокой силе связи между фактором и результатом, следовательно, синтезированная регрессионная модель пригодна для практического использования. Пусть необходимо определить затраты на ремонт оборудования, возраст которого составляет 15 лет.
Методы детерминированного факторного анализа Метод цепных подстановок Пусть дана детерминированная мультипликативная модель. Необходимо определить размер влияния факторов А, В, С на результативный показатель Y. Метод цепных подстановок позволяет определить влияние отдельных факторов на изменения величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя на фактический в отчетном периоде.
Пусть известно базисное значение показателей у0, а0, b0, с0 и отчетное значение показателей у1, а1, b1, с1. Алгоритм метода цепных подстановок состоит из следующих шагов: 1) расчет значений результативного показателя «у». · Расчет базисного значения результативного показателя «у»
· Расчет условных значений показателя «у»
Количество условных показателей на единицу меньше числа факторов модели. · Расчет отчетного значения показателя «у»
2) расчет влияния факторов на результативный показатель «у» · Расчет влияния фактора «а» на результативный показатель «у»
Таким образом, при расчете ∆у(а) факторы b и с зафиксированы на уровне базисного значения. Изменяется только фактор «а», тем самым устранено влияние факторов b и с на показатель «у». В этом сущность приема элиминирования, то есть устранения, нейтрализации влияния на результативный показатель всех факторов кроме одного – исследуемого. · Расчет влияния фактора «b» на результативный показатель «у»
· Расчет влияния фактора «с» на результативный показатель «у»
3) Проверка – контроль правильности расчетов. Изменение результативного показателя «у» можно определить двумя способами: · ∆ · Изменение показателя «у» есть сумма его изменений за счет каждого из факторов ∆ Расчеты произведены верно, если ∆ у1 = ∆ у2 4) Выводы. Метод абсолютных разниц При использовании метода абсолютных разниц величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую величину факторов, которые находятся с права от него и на фактическую величину факторов, расположенных слева от него в модели. Подсчет строится на последовательной замене плановых значений факторных показателей на их отклонение, а затем на фактический уровень этих показателей. Пусть дана факторная мультипликативная модель ∆ ∆ ∆ В заключении необходимо осуществить контроль правильности расчетов (п.3 метод цепных подстановок) и сделать выводы. Метод относительных разниц Для расчета влияния первого фактора необходимо базисную (плановую величину) результативного показателя «х» умножить на относительную величину прироста первого фактора выраженную в процентах и результат разделить на 100. Пусть дана факторная мультипликативная модель ∆ Определим изменение результативного показателя «у» за счет каждого из факторов.
После окончания расчетов необходимо осуществить контроль правильности расчетов (п.3 метод цепных подстановок) и сделать выводы. Индексный метод Данный метод основан на относительном показателе – динамики выполнения плана. Пусть дана двухфакторная мультипликативная модель у = а * b. Индекс результативного показателя «у» рассчитывается следующим образом. Индекс фактора «а» рассчитывается следующим образом:
Индекс фактора «b» рассчитывается следующим образом: Расчеты произведены верно, если Jy = Ja * Jb. Индекс фактора «а» показывает как изменилась динамика результативного показателя за счет фактора «а». Нетрудно убедиться в том, что если из числителей, приведенных в выражении для вычисления индекса вычесть знаменатели, то получаться абсолютные приросты результативного показателя в целом и за счет каждого из факторов.
Интегральный способ Элиминирование имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом деле они взаимосвязаны и в результате этого взаимодействия получает дополнительный прирост результат показателя, который при изменении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на результативный показатель меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели. Интегральный метод частично компенсирует этот недостаток. Формула интегрального метода для двухфакторной модели: у = а * b.
∆а = а1 – а0; ∆b = b1 – b0 Для трехфакторной модели: у = а * b * с
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.67.90 (0.008 с.) |

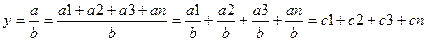

 , где a/c = d1; b/c = d2
, где a/c = d1; b/c = d2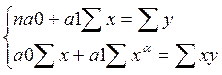
 ;
; 

 ;
; 



 ;
; 

 ∆
∆ 



 ∆у(а) + ∆у(b) + ∆у(с)
∆у(а) + ∆у(b) + ∆у(с) и известны значения показателей в базисный у0, а0, b0, с0 и отчетный у1, а1, b1, с1 периоды. Определим влияние каждого из факторов на результативный показатель «у».
и известны значения показателей в базисный у0, а0, b0, с0 и отчетный у1, а1, b1, с1 периоды. Определим влияние каждого из факторов на результативный показатель «у». -- влияние фактора «а»
-- влияние фактора «а» -- влияние фактора «b»
-- влияние фактора «b» -- влияние фактора «c»
-- влияние фактора «c» ; ∆
; ∆ 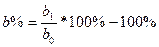 ; ∆
; ∆ 
 -- за счет фактора «а»;
-- за счет фактора «а»; -- за счет фактора «b»;
-- за счет фактора «b»;


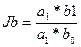



 ;
;  , где
, где После окончания расчетов надо
После окончания расчетов надо провести проверку (см. пункт 3.1.)
провести проверку (см. пункт 3.1.) и сделать выводы.
и сделать выводы.


