
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад розв’язку завдання 2Содержание книги Поиск на нашем сайте Таблиця 6.2.3 Розрахункові дані для обчислення характеристики варіації
Середня кількість вантажних автомобілів для всієї сукупності:
х – середина інтервалу, f – кількість АТП.
Середня кількість вантажних автомобілів для кожної групи окремо:
Таблиця 6.2.4 Дані для обчислення характеристик центру розподілу
Мода:
Модальний інтервал: (65,5-80]
Рис.6.2.1 Графічне зображення моди.
Медіана:
де:
Медіанний інтервал: [36,5-51)
Рис. 6.2.2 Графічне зображення медіани
Показники варіації кількості вантажних автомобілів: Розмах варіації:
Середнє лінійне відхилення:
х – індивідуальне значення ознаки,
f – частота ознаки. Середнє квадратичне відхилення:
Визначаємо дисперсію: А) Як квадрат квадратичного відхилення:
Б) Як різницю квадратів:
В) За методом моментів:
За А вибираємо число, яке знаходиться посередині варіаційного ряду, і – ширина інтервалу. і=14,5 А=(43,75+58,25)/2=51
Коефіцієнт осциляції:
R – розмах варіації,
Квадратичний коефіцієнт варіації:
Оскільки
Групування АТП за виробітком на 100 машинотон: Крок зміни (за виробітком на 100 машинотон):
[124-142,5) = 139, 140, 132, 139, 132, 142, 138, 124. (разом 8) [142,5-161) = 145, 159, 148, 144, 152, 149, 154, 156. (разом 8) [161-179,5) = 163, 175, 170, 162, 167. (разом 5) [179,5-198] = 182, 182, 182, 198. (разом 4) Таблиця 6.2.5 Комбінаційний розподіл АТП за кількістю автомобілів та за виробітком на сто машинотон.
Розрахуємо середній виробіток на 100 машинотон для всієї сукупності: Розрахуємо середній виробіток на 100 машинотон для кожної групи:
Таблиця 6.2.6 Розрахункові дані для обчислення групових дисперсій
Обчислимо внутрішньо групові дисперсії:
n – кількість АТП.
Середня з внутрішньо групових дисперсій:
Міжгрупова дисперсія:
де:
х- загальна середня для всієї сукупності
Перевіримо отриманий результат:
Результати майже збіглися, відхилення виникло за рахунок заокруглень. Обчислимо коефіцієнт детермінації:
це означає що 11,4% загальної дисперсії виробітку на 100 машинотон обумовлене кількістю вантажних автомобілів, а решта зумовлене іншим фактором. Емпіричне кореляційне відношення:
тобто залежність між середнім виробітком на 100 машинотон і кількістю вантажних автомобілів становить 34%. Розрахуємо дисперсію частин АТП третьої групи. Частка підприємств третьої групи складає:
Тоді дисперсія:
Висновок: Згідно обрахунків досліджувана статистична сукупність є неоднорідною. Середня кількість вантажних автомобілів для всієї сукупності становить 51,29. Мода встановилась на рівні 70,33, а медіана 49,79. Обчислення були достатньо точними, про що свідчить невелика розбіжність між значеннями величин обрахованих різними способами. Залежність між середнім виробітком на 100 машинотон і кількістю вантажних автомобілів становить 34%. Методичні рекомендації до завдання З Та приклад розв’язку Динамічний ряд являє собою перелік числових значень певного статистичного показника в послідовні моменти чи періоди часу. Числові значення того чи іншого статистичного показника, які складають динамічний ряд, називаються рівнями ряду (позначаємо Ряди динаміки, як правило, представляють в таблицях або графічно. При графічному зображенні динамічного ряду на осі абсцис будується шкала часу, а на осі ординат - шкала рівнів ряду. При цьому на осі абсцис обов'язково повинен зберігатися (виконуватись) масштаб часу, інакше лінійний графік не вірно відобразить характер зміни. На осі ординат при необхідності можна користуватися перерваною шкалою. В залежності від характеру ряду в статистиці розрізняють слідуючі види динамічних рядів: моментні ряди, інтервальні ряди, ряди середніх величин, ряди відносних величин. Моментним називається ряд, абсолютні рівні якого характеризують величину явища станом на певні моменти, певні дати. Інтерваяьним називається такий ряд, абсолютні рівні якого характеризують величину показника, що вивчається, одержану в підсумку за певний період часу. Відмінною рисою інтервальних рядів є те, що їх рівні можна дробити і сумувати. Наприклад, знаючи число народжених по місяцям, можна скласти ці показники і отримана сума дасть число народжених за рік. Якщо ж кожен місячний рівень поділити на тривалість місяця, то нові рівні дають уявлення про середньодобову народжуваність по місяцям. Подібні дії з рівнями моментного ряду позбавлені змісту. Перш ніж аналізувати динамічний ряд необхідно, виходячи з мети дослідження, переконатися в співставності рівнів ряду за їх змістом, одиницями вимірювання, території, методу розрахунку, а для інтервальних рядів врахувати порівнянність тривалості тих періодів, до яких відноситься даний ряд. У випадку відсутності зіставленості, добитися її додатковими розрахунками (змикання рядів динаміки).
Таблиця 6.3.1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |




 ; де:
; де: =
=  = 28,6;
= 28,6; =
=  = 41,3;
= 41,3; =
=  = 58,5;
= 58,5; =
=  = 72,9.
= 72,9.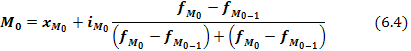 де:
де: - нижня границя модального інтервалу,
- нижня границя модального інтервалу,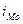 - розмір модального інтервалу,
- розмір модального інтервалу, - частота модального інтервалу,
- частота модального інтервалу, - частота попереднього інтервалу,
- частота попереднього інтервалу, - частота інтервалу наступного за модальним.
- частота інтервалу наступного за модальним.



 - нижня границя медіанного інтервалу,
- нижня границя медіанного інтервалу,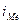 - розмір медіанного інтервалу,
- розмір медіанного інтервалу, - півсума накопичених частот,
- півсума накопичених частот,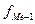 - сума накопичених частот, які передують медіанному інтервалу,
- сума накопичених частот, які передують медіанному інтервалу, - частота медіанного інтервалу.
- частота медіанного інтервалу.





 , де:
, де: - середнє значення ознаки,
- середнє значення ознаки,


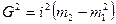 , де
, де  ,
, 
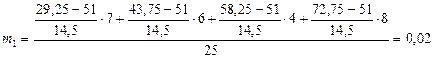


 де:
де:

 > 33%, то статистична сукупність є неоднорідною.
> 33%, то статистична сукупність є неоднорідною.
 т/км
т/км



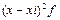
 , де:
, де: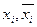 - значення ознак окремих елементів сукупності,
- значення ознак окремих елементів сукупності,





 - групові середні
- групові середні - чисельність окремих груп
- чисельність окремих груп



 ,
,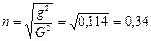 ,
,

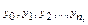 ).
).


