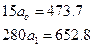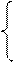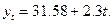Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні характеристики рядів динаміки
Між ланцюговими і базисними коефіцієнтами зростання існує зв'язок: добуток ланцюгових коефіцієнтів дорівнює базисному.
і відношення кожного поточного базисного коефіцієнта зростання до попереднього рівне ланцюговому:
Середній абсолютний приріст:
Середній коефіцієнт зростання:
де Середній темп зростання:
Середній темп приросту:
Середнє абсолютне значення 1% приросту:
Деякі методи вивчення основної тенденції динаміки. Тенденція – це певний напрям розвитку, тривала еволюція, яка набуває більш-менш плавної траєкторії. 1. Зглажування динамічного ряду методом ступінчастої середньої (середньої арифметичної). При застосування цього методу первинні рівня динамічного ряду змінюються середніми по інтервалах.
2. Збільшення періодів і згладжування динамічного ряду методом плинних середніх. Це найбільш простий спосіб перетворення ряду. Суть даного методу полягає в тому, що первинні рівні динамічного ряду замінюються середніми по інтервалах, але при цьому кожний наступний інтервал утворюється з попереднього зміщенням на один рівень.
Таблиця 6.3.2.
Вирівнювання методом ступінчастої середньої
Таблиця 6.3.3. Вирівнювання ряду методом плинних середніх
Він має на меті знайти плавну лінію розвитку (тренд) даного явища, що характеризує основну тенденцію його динаміки. Цей метод використовується, якщо теоретичний аналіз суті явища, яке вивчається, законів його розвитку підказує, що дане явище розвивається в арифметичній прогресії (тобто з приблизно рівними абсолютному приростами). Тоді, як відомо, рівняння прямої лінії може бути виражене формулою:
де Y1- значення рівнів вирівняного ряду, які слід розрахувати;
І, відповідно, завдання зводиться до того, щоб фактичні рівні ряду динаміки (у) замінити теоретичні рівняння (у1) розрахованими на основі наведеного вище рівняння. Це завдання розв’язується за допомогою способу найменших квадратів, суть якого полягає в тому, що пряма, яка вирівнює ряд, повинна проходити максимально близько до фактичних рівнів ряду, тобто сума квадратів відхилень (фактичних рівнів від теоретичних) повинна бути найменшою: Спосіб найменших квадратів дає систему двох нормальних рівнянь для знаходження параметрів а0 і а1 шуканої прямої лінії:
де y – рівні фактичного ряду динаміки;
n – число членів ряду. Оскільки значення t є показником часу, то завжди можна їм надати такого значення, щоб їх сума дорівнювала нулю значно. При цьому система значно спроститься:
Звідси
Таким чином, теоретичні рівні легко обчислити.
Використовуючи дані таблиці одержимо:
Розв’язування одержаної системи рівнянь дає наступні значення параметрів шуканої прямої:
Таблиця 6.3.4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.195.24 (0.015 с.) |
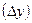 вказує на скільки одиниць в абсолютному вираженні рівень одного періоду більше чи менше попереднього або базисного рівня і, відповідно, може мати знак " + " (при збільшенні рівнів) чи " — " (при зменшенні рівнів).
вказує на скільки одиниць в абсолютному вираженні рівень одного періоду більше чи менше попереднього або базисного рівня і, відповідно, може мати знак " + " (при збільшенні рівнів) чи " — " (при зменшенні рівнів).
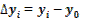
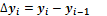
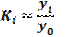
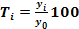
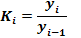
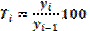
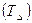 - відносний показник, що показує на скільки процентів один рівень більше (чи менше) попереднього або базисного рівня.
- відносний показник, що показує на скільки процентів один рівень більше (чи менше) попереднього або базисного рівня.
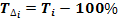 або
або
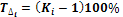
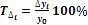
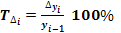
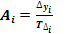 або
або
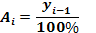
 (6.20)
(6.20)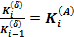
 (6.21)
(6.21)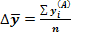 або
або 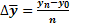 (6.22)
(6.22)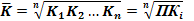 або
або 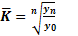 (6.23)
(6.23)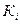 - ланцюгові коефіцієнти зростання.
- ланцюгові коефіцієнти зростання.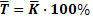 (6.24)
(6.24)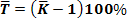 або
або 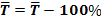 (6.25)
(6.25)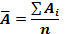 (6.26)
(6.26)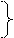 16,5
20,2
27,7
16,5
20,2
27,7
 16,5
16,5
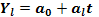 (6.27)
(6.27)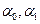 - параметри прямої;
- параметри прямої;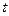 - показники часу (дні, місяці, роки і т.д.).
- показники часу (дні, місяці, роки і т.д.).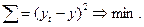
 (6.28)
(6.28) (6.29)
(6.29)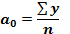 і
і 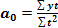
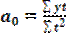 (6.30)
(6.30)